螺旋曲面通道内组合涡发生器的强化传热及优化研究*

张亚龙，刘升学，卿德藩，王翠芳

(南华大学 机械工程学院，湖南 衡阳 421001)

1 引 言

工业上普遍采用的换热器是一种典型的流体设备，研究换热器内流体流动及其对传热性能的影响具有很高的应用价值。此外在换热器内设置涡发生器改变流体流动方向，促进传热，长期以来一直是人们研究的重点。

由于换热器内涡发生器的几何形状、尺寸与布置方式不同时，其换热能力就会有较大差异。如吕静[1]认为三角翼的换热性能优于矩形翼。JoardarA[2]发现，与顺排的涡发生器相比，叉排涡发生器的传热效果较好，而压力损失却减小。Kwak KM[3]比较了三排三角翼顺流排列与逆流排列时的流动与换热特性。发现三角翼顺逆流是传热效果明显增强。一些研究者对柱状(例如圆柱、椭圆柱等)涡流发生器进行了试验研究,均取得了良好的效果[4]。

上述学者分别研究了三角翼或者柱状涡发生器的阻力特性和强化传热性能,但差别较大。因此，本文在前人研究的基础之上，以螺旋曲面通道内设置三角翼和椭圆柱两种组合形式的涡发生器进行研究，从

数值模拟和实验两方面探究涡发生器流动控制机理的特性。从而，分析不同涡发生器产生的涡旋特性及其发展机理，研究强化传热和流动特性的影响规律。

2 通道结构与物理模型设计

选择型号为16T120-1.2/1400-10的螺旋板式换热器为计算模型，原始结构参数为：通道宽度d=10 mm，壁面厚度δ=2 mm，通道高度D=1.17 m，初始半径Ri=145 mm，通道圈数N=40[5]。对于三角翼的大小，由于受螺旋通道间距的限制，翼高不超过10 mm，根据模型实际需求，在实验雷诺数范围下取三角形H1=6mm，L=8 mm[5]。对于椭圆柱，由于具有抗压作用，取高度为10 mm，2a=12 mm，2b=3 mm。

此项研究采用组合纵向涡发生器(CLVG)由如图1所示的直角三角翼和椭圆柱两种形状组合而成，放置在螺旋板式换热器通道管壁上。研究组合间距s、三角翼攻角α、椭圆柱攻角β对换热影响。

3 计算模型选取及模拟结果

3.1 计算区域的选取

计算模型如图2所示。

由于换热器结构复杂，为了加快收敛速度，考虑到结构的对称性，选取图2中组合区域300 mm×200 mm为计算区域。入口段距边界延长1.5倍通道间距，保证入口流速均匀，出口延长2.5倍的通道间距，防止回流。螺旋面为换热表面，材质为2 mm的不锈钢板，不考虑自身导热，流道的两侧和上下面均对称，表面为光滑的绝热材料，涡发生器材质与螺旋板相同。

图1 涡发生器结构示意图

图2 计算模型

3.2 相关控制方程及边界条件设置

计算时控制方程的离散多采用控制容积积分法，扩散项采用中心差分格式，对流项离散采用Second Order Upwind格式，压力和速度的藕合采用SIMPLEC算法，该算法相对于SIMPLE算法更易于收敛且通常能够得到更好的结果，而对于PISO算法则会节省每个迭代步骤中所要花费的CPU时间[5]。

文中采用超松弛迭代法对计算的控制微分方程进行迭代，迭代收敛性判据如下：

‖ui-ui-1‖/‖ui‖≤εu

(1)

‖R(ui)‖/‖R(u0)‖≤εp

(2)

其中：║·║表示范数；ui为经i次迭代收敛后矢量；εu、εp为允许误差；R为残余矢量。

一般当收敛同时满足这两个判据时，动量和能量方程的相对余量均小于10-8，迭代收敛。

热流介质为water-vapor [H2O],冷流介质为空气，其相应物性参数如密度、黏度等均按默认值。

计算区域边界条件设置如下:

(1) 入口边界：选择速度入口，流速分布均匀。水蒸汽温度为400 K，空气入口温度为293 K。湍流强度I=0.16(ReDH)-1/8，其中DH表水力直径。

(2) 出口边界：选择压力出口，由Fluent得出出口其余条件值。

(3) 壁面边界：选择速度无滑移边界u=0。

(4) 其余条件：根据模型大小及网格划分情况，预先设定迭代次数为200,三角翼和椭圆柱壁面为速度无滑移固体面，温度由换热器耦合计算得出[6-8]。

3.3 数值模拟结果

使用Fluent软件进行数值模拟，椭圆柱a/b=4与组合涡发生器压力图如图3所示。

图3 涡发生器压力图

由图3(a) 、(b)看出：组合涡发生器改变压力分布，说明在螺旋通道内流体速度发生剧烈变化，产生的纵向涡旋带动卷吸壁面滞流区流体旋转冲刷壁面，破坏了热边界层，也增大了湍流强度；椭圆柱a/b=4的涡发生器压力分布区域较大且不明显。因此，组合涡发生器的强化传热效果优于单独布置椭圆柱涡发生器。

3.4 三角翼攻角α对换热的影响

研究三角翼攻角对螺旋通道换热和流体流动的影响，固定其它参数(β=45°，s=80 mm)，取α=30°、45°、60°三种情况进行数值模拟。图4、图5不同攻角α时平均Nu、阻力系数f随Re变化图。

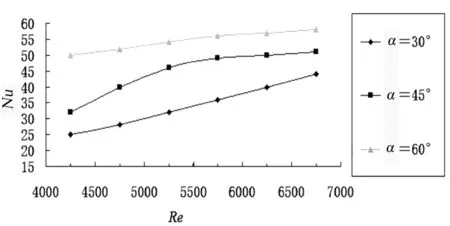
图4 不同攻角α时平均Nu数随Re变化

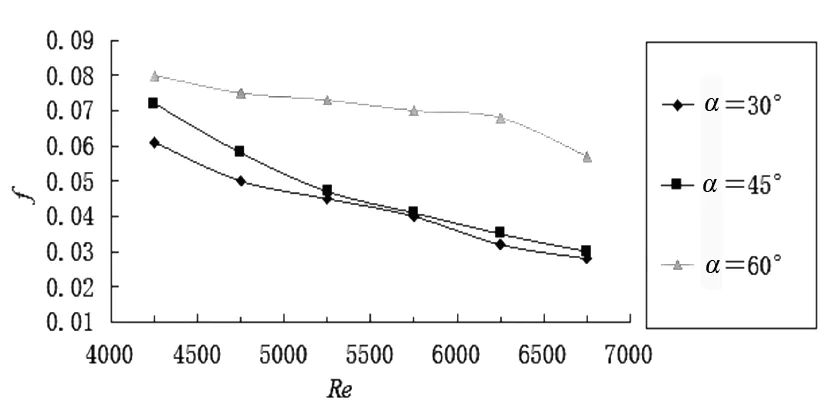
图5 不同攻角α时阻力系数f随Re变化图

可以看出不同攻角情况下，表面平均Nu数均随Re数增加而增大，而阻力系数f则随Re数增加而减小。同时在同一工况Re=4 750之后，α=45°变化最大，之后趋于平稳增长。此时，α=60°时的Nu数最大，说明换热效果最好，α=60°平均Nu数分别比α=45°高23.4%，比α=30°高45.1%。图5表明阻力系数f在α=60°时最大即阻力最大，能量耗损最大，显然不利于换热。同样，在工况Re=4 750下，各阻力系数均呈现稳定下降趋势，在Re=5 250之后，α=45°与α=30°的阻力相差不大。因此，三角翼攻角α=45°时综合传热性能较好。

3.5 椭圆柱攻角β对换热的影响

分析椭圆柱的攻角对螺旋通道换热和流体流动性能的影响规律，固定参数(α=45°，s=80 mm)，在椭圆柱迎流攻角β=30°、45°、60°时分别进行数值模拟研究。图6、图7为不同攻角β时平均Nu、阻力系数f随Re变化图。

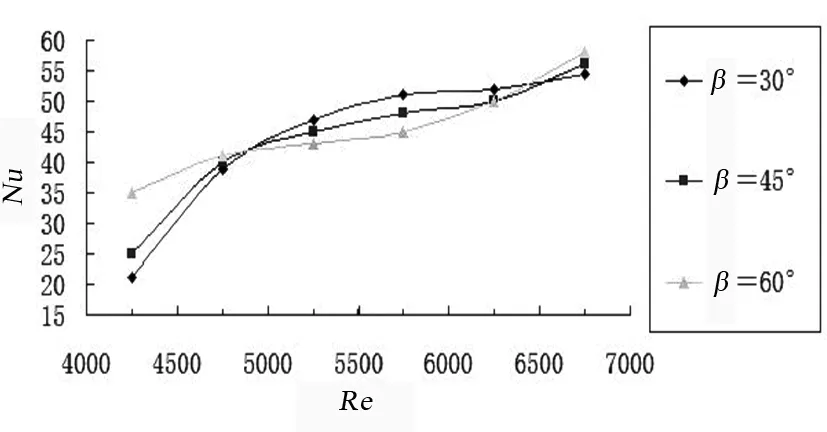
图6 不同攻角β时平均Nu数随Re变化图

图7 不同攻角β时阻力系数f随Re变化图

三者平均Nu数均随着Re数增加而增大，阻力系数f则减小。当Re在4 750与6 250之间变化时，β=60°的努塞尔数Nu小于45°和30°的情况，说明在这一流速范围内，攻角β=60°工况下，产生横向涡个数多于纵向涡，总体热交换强度就弱。对比图7可看出，相同雷诺数Re下，β=45°的阻力系数最低。综合考虑，β=45°时强化传热效果最好。

3.6 组合间距s对换热的影响

固定其它参数(α=45°，β=45°)，只改变间距进行数值模拟，涡发生器的间距分别取80 mm、90 mm、100 mm 。图8、图9为不同间距s时平均Nu数、阻力系数f随雷诺数Re变化图。

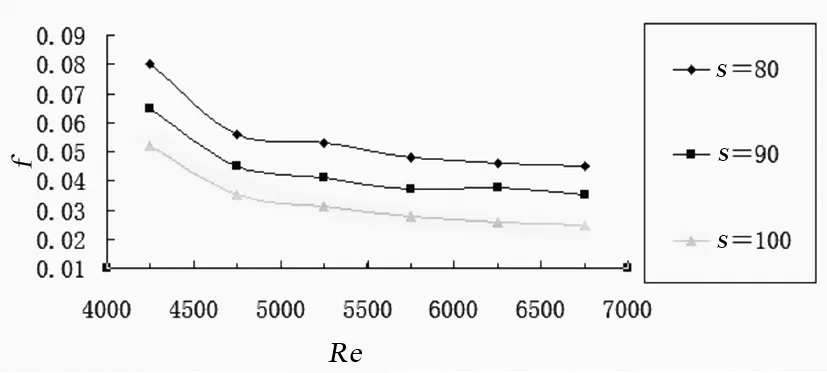
图8 不同间距s时平均Nu数随雷诺数Re变化图

图9 不同间距s时阻力系数f随雷诺数Re变化图

可以看出布置多排涡发生器时排列间距对换热与阻力特性的影响比较明显。总体来观察两个图的数据变化，平均Nu数均随雷诺数Re增大而增大，大小顺序依次为：s=90 mm最大，其次是s=80 mm，s=100 mm最小，而阻力系数s=100 mm最小，s=80 mm最大。所以综合考虑s=90 mm时，效果较好。

4 组合结构优化与实验测试

4.1 组合涡发生器结果优化

通过上述研究，为了更好地得出最优结构，在上述结论的基础上制定因素水平表，分别用A、B、C表示。由前文可知，三个因素的独立影响较优参数分别为s=90 mm、α=45°、β=45°，因此，取Re=5 000时，本次正交试验设计的水平在这些较优数值的周边确定为3个的水平因素表，如表1所示。

表1 因素水平表

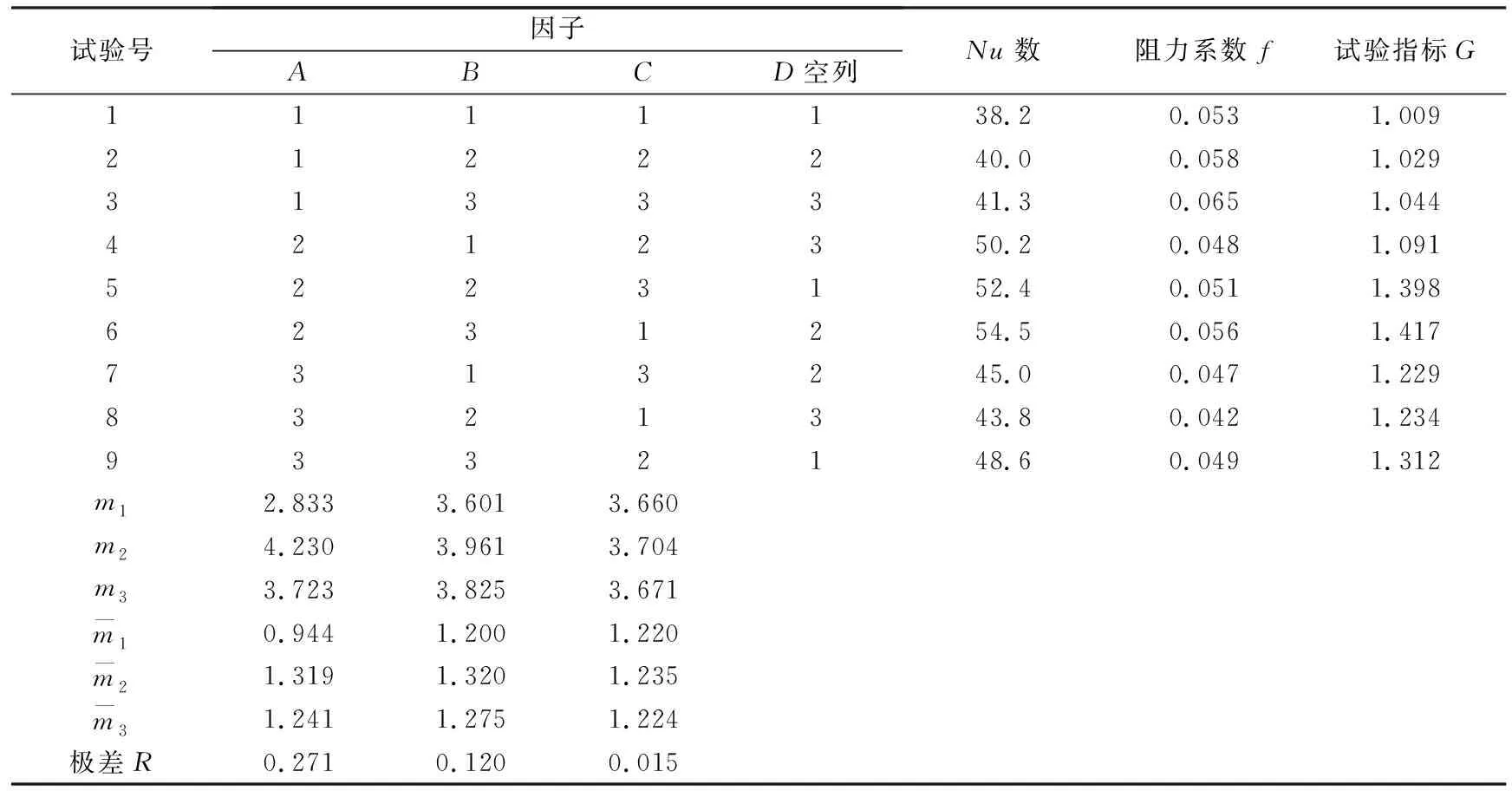
表2 试验结果分析表

为了准确表示优化结构强化传热的程度，对数值模拟的结果利用强化传热判定准则作进一步计算，应用工作效应对比评价准则数G[9]，其判定公式为：

(3)

式中：Nu为强化型努塞尔数；f为阻力系数；Nu0为普通型换热器努塞尔数。下标“0”代表无强化的情况。得出综合评价指标G(试验指标)随雷诺数Re变化曲线，如图10所示。

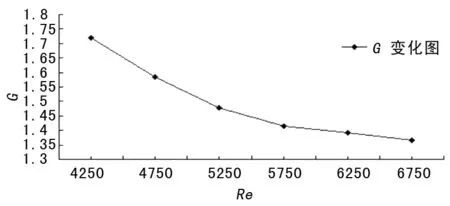
图10 综合评价指标曲线

可以看出，随着Re值的增大，G值呈下降趋势。与优化结构的强化传热基本相吻合。

4.2 实验测试及分析

优化结构与常规结构如图11所示。实验测试的系统简图如图12所示。

图11 通道模型实物图

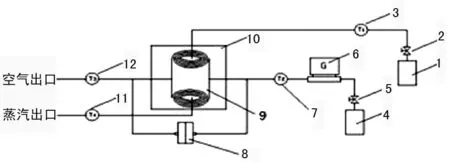
图12 实验系统简图1.全自动电蒸汽锅炉 2、5.阀门 3、7、11、12.热电偶温度计 4.蜗杆式空气压缩机 6.流量计 8.U型压力计 9.螺旋板式换热器模型 10.保温箱

为验证优化效果，采用实验研究方法对上述最优结构进行实验测试。实验流程如图12所示，工作过程为：全自动蒸气锅炉1产出蒸气流经阀门2和热电偶温度计3进入实验测试系统再经温度计11流向蒸气出口；蜗杆式空气压缩机4将空气流经阀门5、流量计6和热电偶温度计7进入实验测试系统再经温度计12流向空气出口，热电偶温度计分别测进、出口蒸汽温度，流量计测进口端的空气流速。其中，测试系统由保温箱10、换热板试件9和U型压力计8组成，试件是用普通型和优化型进行更换测试，U型压力计用来测量测试系统空气进出两侧的压差。

为了比较优化结构与常规结构换热效果及验证模拟结果准确性，文中根据实验结果总结出二者在不同实验雷诺数下总换热系数K变化曲线及压降ΔP的沿程曲线与模拟结果对比图，如图13、14所示。

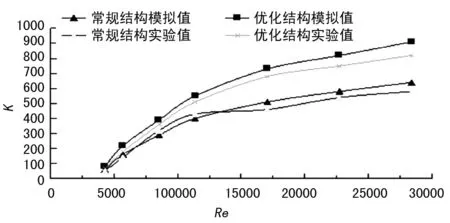
图13 换热系数K随Re变化曲线图

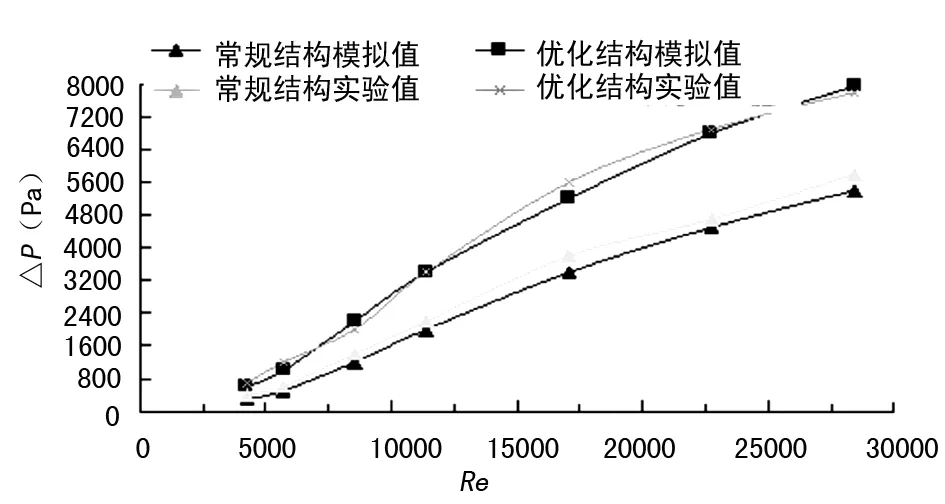
图14 压降ΔP随Re变化的沿程曲线图

由图13、14可看出，换热器总换热系数K和压力降ΔP均随雷诺数Re的增大而增大。压降的增加与总换热系数相似，二者都是在雷诺数Re=4 000之后，尤其是压降图几乎呈直线上升，说明在较低雷诺数下，涡旋产生的强度及尺寸都较小，故对边界层的扰动程度不够明显，压降较小。而随着雷诺数的增加，流体介质对换热壁面及边界层的扰流程度增加，涡旋产生的二次流能卷吸换热壁面的滞流体即螺旋通道的湍流度变大，换热效果增强。观察图14压降曲线的曲率变化可知，优化结构的换热器曲率变化较大，扰流程度明显优于常规换热器。同时，从图13、14中还可得出，优化结构的实验值与模拟值误差均在5%～8%之间，在误差允许范围内两者吻合，证明文中采用的数值模拟方法及模型与实际情况较一致。

5 结 论

(1) 数值模拟结果显示组合涡发生器的结构参数即两种涡发生器的攻角和组合间距对换热通道表面的流动特性与传热性能影响很大，并且得出一组组合结构参数α=45°，β=45°，s=90 mm，其综合换热效果最优。

(2) 对优化组与常规组进行数值模拟及实验研究对比，并计算得出优化组的换热器换热系数明显高于常规组，其传热特性及压降特性范围的实验结果与数值模拟结果较为吻合。

参考文献：

[1] 吕 静，王中铮．利用纵向涡旋发生元强化传热 [J]．暖通空调，2001，31(5)：47-48．

[2] Joardar A，Jacobi A M．Impact of Leading Edge Delta-Wing Vortex Generators on the Thermal Performance of a Flat Tube，Louvered-fin compact Heat Exchanger [J]．Int J Heat Mass Transfer，2005(48)：1 480-1 493．

[3] Kwak K M，Torii K，Nishino K．Simulataneous Heat Transfer Enhancement and Pressure Loss Reduction for Finned-tube Bundles with the First Or Two Transverse Rows of Built-in Winglets [J]．Experimental Thermal and Fluid Science，2005(29)：635-632．

[4] Tiggelbeckst, Mitrank, Fiebigm. Experimental Investigations of Heat Transfer Enhancement and Flow Losses in A Channel With Double rows of longitudinal Vortex Generators [J]. Heat Mass Transfer, 1993, 36(9): 2327-2337.

[5] 王翠芳,刘升学.组合涡发生器在螺旋板式换热器上的强化传热研究[J].机械研究与应用,2012,120(4):29-32.

[6] Gilles D, Alberto F. Laminar Natural Convection in a Vertical Isothermal Channel with Symmetric Surface Mounted Rectangular Ribs[J]. mt J Heat and Mass Transfer, 2002, 23(4):519-529.

[7] 魏 晋，齐承英．纵向涡发生器强化换热性能的数值研究[J]．河北工业大学学报，2006,35(6):88-91.

[8] 杨泽亮，吴欣颖．纵向涡强化竖直平板自然对流换热的数值模拟[J]．华南理工大学学报(自然科学版)，2006 ,34(12):115-118.

[9] 林宗虎.强化传热及其工程应用[M].北京：机械工业出版社，1987.