数据重采样技术在振动信号分析中的应用与试验*

岳晓峰，李 帅

(长春工业大学 机电工程学院，吉林 长春 130012)

1 引 言

变速箱在汽车传动系统中的重要性是不言而喻的，其地位仅次于发动机。通过档位的变换，变速箱可在发动机和车轮之间产生不同的变速比，使发动机的动力性能得到最佳传输。由于变速箱其构成零部件如齿轮、轴承和轴等加工工艺复杂，装配精度高，且常在高速、重载的环境下连续工作，所以变速箱发生故障的概率也较高，此外对变速器性能要求的不断提高，使得其构造系统越来越复杂，从而对其进行精密诊断分析的难度也越来越大。因此实时在线监测及故障诊断的应用对于变速箱的故障诊断有着十分重要的意义，其中变速箱状态检测及故障诊断的有效方法之一便是振动分析。

在变速箱中，随着转速的变化许多机械特性也发生变化，有些机械缺陷的获得需要在转速达到或超过临界转速的条件下。因此在振动测试中对机械进行升速或降速是必不可少的。然而每个独立谐波的频带随着转速的变化将会变宽，一些频率分量产生重叠的现象，运用传统的FFT功率谱进行特征振动分量分析时，分析结果会变得模糊不清。为此必须利用阶次分析的方法，将等时间间隔采样的振动信号转化为等角度间隔采样的振动信号，从而获得不随转速变化的平稳的振动信号，再利用傅里叶变换分析。振动信号的重采样则是该方法中不可或缺的一个环节。

2 重采样的基本原理

重采样的原理电路图如图1所示。

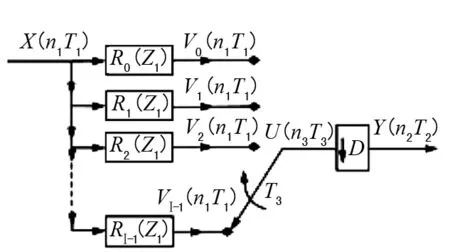
图1 重采样的原理电路

由图1可得出,当输入一个X(n1T1)时,经过内插和滤波便会产生I个相位间隔均匀的数据,其中的VI-1(n1T1)是最先输出的，究其原因是因为其相位超前,V0(n1T1)则最后一个输出。下一个X(n1T1)输入后,最先输出又是VI-1(n1T1),最后输出依然是V0(n1T1), 输出序列U(n3T3) 经过如此循环便会产生,然后经过D倍的抽取序列U(n3T3)被转化成序列Y(n2T2)。由于每隔D-1个数据才从序列U(n3T3)中抽取一个数据,所以不用计算每一个数据，只计算被抽取出的数据即可,可见确定在什么时候计算哪一个数据才是重采样技术的关键,由此可得到重采样的实现电路如图2所示。其中什么时候计算由图2中的运算控制来确定，计算哪个数据则决定于滤波器多相分量的系数，而多相分量的系数的选择则由图2中的相位控制来确定[1]。

图2 重采样的实现电路

3 重采样的应用

变速箱状态检测及故障诊断中需要对变速箱进行升速和降速，而传统的频谱分析只能对匀速的机械产生的等时间间隔的振动信号进行分析，所以为了达到检测及故障诊断的目的，消除变速箱速度变化时产生的频率分量重叠现象，研究人员就一定要对预分析信号进行重采样，图3为等时间间隔的采样，其作用是消除“频率模糊”现象[2]可以发现在图中，每个周期内的采样数随着频率的增加，其采样数越来越少。图4为等角度间隔的采样，当频率发生变化时，单周期内的采样数不会发生变化。

图3 等时间间隔采样 图4 等角度间隔采样

通过硬件设备和软件系统均可以实现重采样的过程，早期的研究中应用硬件系统来实现重采样，但硬件系统有诸多缺点，首先其价格非常高昂，其次其构造组成复杂，最后其工作环境也有很大的限定，测量工作需要在转速较低的情况下在可以完成近年随着来软件技术的不断发展，软件在重采样技中的应用越来越广泛，正逐步取代硬件设施。

基于变速箱转速信号以及振动信号的同步采集的基础，利用转速的脉冲数来计算在每转插入的阶次，从采样时刻来实现振动信号的重采样[3]。实现重采样的数学算法如下：

假设轴做匀加速运动，转角为θ，可以利用如下公式来表示：

θ(t)=b0+b1t+b2t2

(1)

其中：b0、b1、b2为未知系数，t为采样时间。

在时域中，假设Δψ为一个脉冲信号对应的轴转过的角度增量，那么3个未知系数就可以通过拟合3个连续的脉冲到达时间t1、t2、t3得到：

(2)

将式(2)带到式(1)中，便可得到式(3)：

(3)

将3个逐步达到脉冲时间点的t1、t2、t3带入式(3)中，就能够求出未知系数b0、b1、b2的值，将它们带入(1)中，可以得到角增量Δθ所对应的时间t，即得到公式(4)：

(4)

式中：k为插值系数，由此得到公式(5):

θ=kΔθ

(5)

通过式(4)得出重采样的时间序列，然后对振动信号做插值处理，最后得出它所对应的幅值，从而实现了重采样的过程，得到了与转速同步的振动信号的采样信号[4]。

国外有关学者对重采样经行了比较全面的研究表示阶次分析的精度取决于以下几个方面[5]：①发出脉冲信号的设备精度和分辨率的高低；②轴的转速是否能够在有效范围之内；③数字信号的拟合和插值精度的高低等。

4 实验仿真

振动信号的基频会随着变速箱输入轴转速的变化而发生改变，因而致使每个独立谐波的频带带宽变宽。独立频带变宽，意味着一些频率分量有重叠的现象发生。普通频谱分析因为功率谱频率重叠变得模糊，所以就不能用以鉴别特征振动分量。

在转速为6 000～0 r/min的降速情况下，通过模拟的振动信号，观察了常用谱分析方法的效果，其信号构成如表1所列。

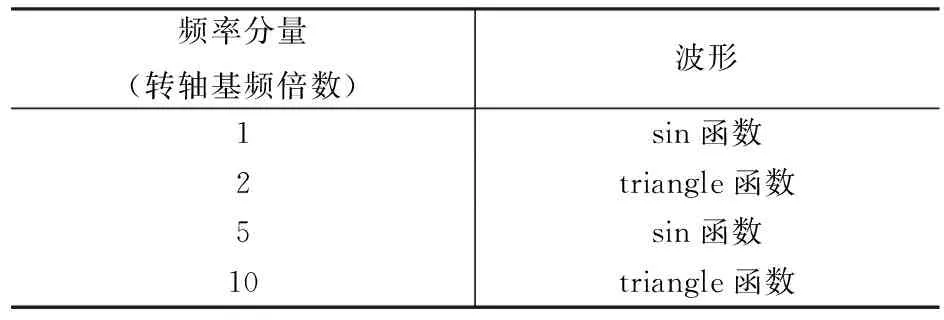
表1 模拟信号频率组成

其振动信号和转速信号如图5～6所示。相应频带的宽度会随着转速的变化而发生变化。相应谐波的频率会随着机械零件对应的频率范围变宽而变宽，因而导致常规功率谱中的频率发生混叠的现象，同时常规功率谱的振动周期也发生变化，如图7所示。因此在转速变化的情况下，由于频带变宽而相互混叠，常规功率谱分析不能有效的分离出特征频率，难以获取有效的信息。

图5 振动信号

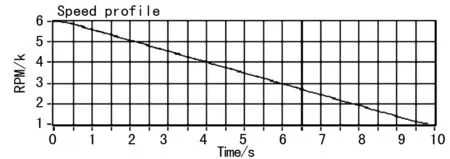
图6 速度信号

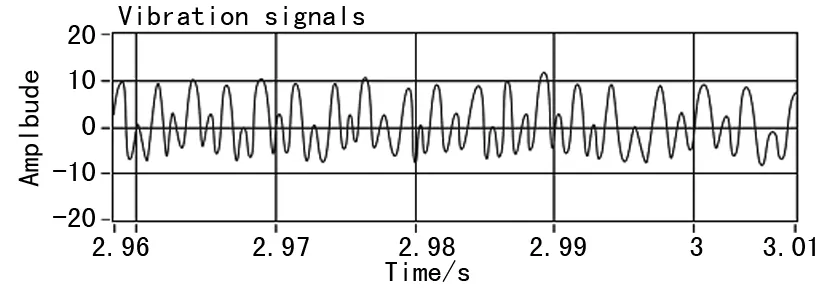
图7 常规功率谱振动信号

利用重采样的方法，使振动信号角域平均，虽然模拟的转速发生了变化，但其峰值并未随之改变，始终在1、2、5、10阶处，同初始设定的情况完全一致。在转速发生变化的情况下，其特征分量的频带宽度没有发生变化，说明没有频率混叠的情况出现，把变速过程的频谱分析视同匀速的过程。同时，其振动周期没有发生变化如图8所示。

图8 角域平均功率谱震动信号

对图5中信号进行常规的FFT功率谱分析，可看出在其转速下降的情况下，常规的功率谱不能对周期分量进行表达如图9所示，振动信号经重采样后，阶次取代了频率成为横坐标，能够看出转轴的基频倍数出现在1、2、5、10阶处，如图10结果所示，由此可见对于重采样振动信号分析的重要性。

图9 FFT功率谱

图10 阶次功率谱

5 结 论

对比重采样前后的功率谱振动图像以及 FFT功率谱图像和阶次功率谱图像可见，基于重采样的方法将等时间的振动信号转化为等角度间隔的振动信号，消除了由于转速变化致使独立谐波的频带变宽，一些频率分量产生重叠的现象，从而可以分离出特征频率，获得有效的信息。对于变速情况下振动信号的分析具有重要意义。

参考文献：

[1] 宗志毅，王晓音，杨莘元.多率信号处理中的重采样技术[J].电子对抗技术，2003，5，18(3):37-41.

[2] 田 吴,栾军英,田 广.阶次跟踪分析在齿面磨损故障诊断中的应用[J].军械工程学院学报，2005，7(5):56-57.

[3] 汪 伟,杨通强,王 红,等.非稳态信号计算阶次分析中的重采样率研究[J].振动、测试与诊断，2009，29(3):349-351.

[4] 汪 伟,杨通强,郑海起,等.利用HHT和重采样技术分析瞬态机械信号[J].机械科学与技术，2007，26(6):741-745.

[5] 任明章,连小珉,蒋孝煜.齿轮箱噪音诊断专家系统的研究与开发[J].清华大学学报(自然科学版)，1996，36(8):66-71.