SWBR0-代数的蕴涵理想及其诱导的商代数
汪 宁, 吴洪博
(陕西师范大学 数学与信息科学学院, 西安 710062)
随着模糊命题逻辑系统的发展, 各种模糊逻辑代数相继出现. 吴望名[1]提出了Fuzzy蕴涵代数(简称FI代数), 并讨论了正则FI代数和HFI代数. 徐扬[2]将格与蕴涵代数结合在一起, 建立了格蕴涵代数. 王国俊[3]提出了模糊命题演算的形式演绎系统L*, 建立了R0-代数[4-5]. Hjek[6]提出了BL-逻辑代数. Esteva等[7]提出了另一种形式系统MTL, 并且提出了相应的MTL-代数. 吴洪博[8]提出了基础R0-代数(BR0-代数), 通过对BR0-代数的研究, 给出了BR0-代数的一种无序表示形式, 并将这种无序表示形式进行弱化, 提出了WBR0-代数[9]. 程国胜[10]引入了R0-代数的滤子和理想.文献[11]讨论了WBR0-代数的正则性与其他逻辑代数的关系; 文献[12]研究了Fuzzy商代数与同态基本定理. 本文基于WBR0-代数的结构特征, 通过将其正则性条件弱化, 建立了SWBR0-代数, 并在此基础上提出了SWBR0-代数蕴涵理想的概念, 讨论了由蕴涵理想诱导的商代数, 研究了其基本性质,得到了SWBR0-代数的同态基本定理.
1 SWBR0-代数及基本性质
在WBR0-代数[9]定义中, 条件(b→0)→(a→0)=a→b体现了该代数结构的正则性[11]. 因为正则性要求特别强, 例如BL-代数、 MTL-代数、 Heyting代数等逻辑代数均不满足正则性质, 因此, 当考虑WBR0-代数更广泛的应用时, 需要将正则性质进行弱化或删除. 本文先将WBR0-代数中的正则性条件(b→0)→(a→0)=a→b进行删除, 提出了SWBR0-代数的概念.
定义1一个(2,2,0,0)型代数(M,(⊕,→,0,1))称为SWBR0-代数是指∀a,b,c∈M, 下列条件成立:
(S1)a⊕0=a;
(S2)a⊕b=b⊕a;
(S3)a→(b→c)=b→(a→c);
(S4) (b→c)→((a→b)→(a→c))=1;
(S5)a→(a⊕b)=1;
(S6) (a⊕b)→c=(((a→c)→0)⊕((b→c)→0))→0;
(S7) 1→a=a;
(S8) 若a→b=1,b→a=1, 则a=b.
根据文献[9]知, SWBR0-代数(M,(⊕,→,0,1))是WBR0-代数当且仅当: ∀a,b∈M, 下列条件成立:
(S9)a→b=(b→0)→(a→0).
性质1设M是SWBR0-代数, ∀a∈M, 则有:
1) 0→a=1;
2)a→1=1;
3)a→a=1;
4)a→((a→0)→0)=1;
5)a→0=((a→0)→0)→0.
证明: 1) 由文献[9]知, 0→a=1成立.
2) 由(S3),(S4)得(0→1)→((1→a)→(0→a))=1, 再结合1)和(S7)得1=1→(a→1)=a→1, 即a→1=1.
3) 由(S1),(S5)得a→a=a→(a⊕0)=1.
4) 由(S3)和3)得a→((a→0)→0)=(a→0)→(a→0)=1.
5) 由4)得a→((a→0)→0)=1, 结合(S4)得(a→((a→0)→0))→((((a→0)→0)→0)→(a→0))=1. 由(S7)得(((a→0)→0)→0)→(a→0)=1. 又由4)得(a→0)→(((a→0)→0)→0)=1, 则由(S8)得a→0=((a→0)→0)→0.
命题1设M是SWBR0-代数, 定义关系≤: ∀a,b∈M,a≤b当且仅当a→b=1, 则:
1) ≤是M上的偏序关系;
2) 0,1分别是M中的最小元和最大元;
3) ∀a,b,c∈M, 若a≤b, 则c→a≤c→b,b→c≤a→c;
4) ∀a,b∈M, 则a⊕b是a和b的上确界.
证明: 1),3),4)在NBR0-代数或WBR0-代数中已证明, 但证明过程并未涉及(S9)[9], 再结合SWBR0-代数的定义知, 结论成立.
2) 由1)及性质1中1),2)知, 结论成立.
2 SWBR0-代数的蕴涵理想
定义2设M是SWBR0-代数,D是M的一个子集, 若∀x,y∈M, 下列条件成立, 则称D为M上的一个蕴涵理想:
1) 0∈D;
2) 若y∈D, (x→y)→0∈D, 则x∈D.

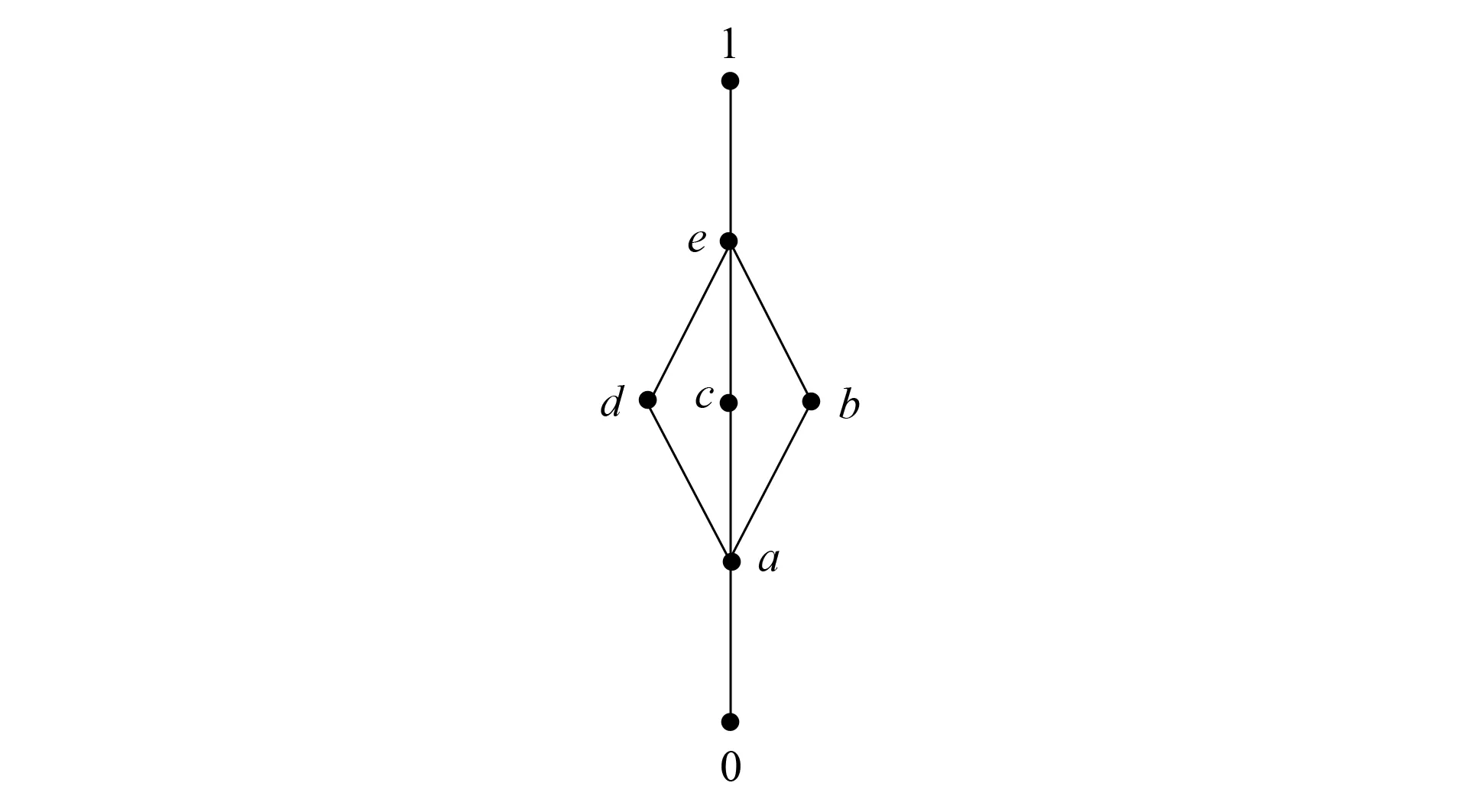
图1 格MFig.1 Lattice M
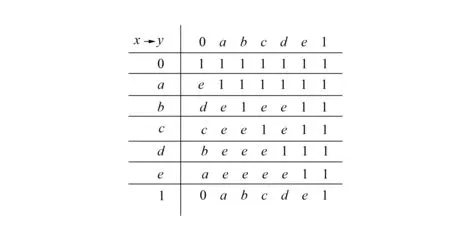
图2 →运算Fig.2 Implication operator
由文献[13]知,M是一个SWBR0-代数. 令D={0,a,b}, 则容易验证D是M的蕴涵理想.
命题2设M是SWBR0-代数,D是M的一个蕴涵理想, 则:
1) 若y∈D,x≤y, 则x∈D;
2) 若(x→0)→0∈D, 则x∈D;
3) 若x→y∈D, 则y∈D;
证明: 1) 由x≤y得x→y=1, 从而由(S7)得(x→y)→0=1→0=0∈D, 又y∈D, 所以x∈D.
2) 由定义2知,x∈D.
3) 由(S3)和性质1中2),3)知,y→(x→y)=x→(y→y)=1, 则y≤x→y. 又x→y∈D, 由1)知,y∈D.
定理1设M是SWBR0-代数,D是M的一个非空集合, 则下列条件等价:
1)D是M的蕴涵理想;
2) ∀x,y,z∈M, 若x∈D,y∈D, 且y≥(z→x)→0, 则z∈D.
证明: 1)⟹2). 因为y∈D, (z→x)→0≤y, 所以由命题2中1)知, (z→x)→0∈D. 又x∈D, 则由定义2知,z∈D.
2)⟹1). ① 因为D≠Ø, 所以∃x∈D. 由命题1中2)知,x≥0. 又由性质1中1)和(S7)知, (0→x)→0=1→0=0, 则x≥(0→x)→0, 故由2)知, 0∈D.
② 设w∈D, (v→w)→0∈D. 因为(v→w)→0≥(v→w)→0, 所以由2)知,v∈D.
定义3设M是SWBR0-代数, 如果~满足下列条件, 则称~是M上的同余关系:
1) ~是等价关系;
2) ~被M上的运算→,⊕所保持, 即∀x,y,z,w∈M, 若x~y,z~w, 则x→z~y→w,x⊕z~y⊕w.
命题3设~是SWBR0-代数M上的同余关系, 则D~={a∈Ma~0}是M上的蕴涵理想.
证明: 1) 因为0~0, 所以0∈D~.
2) 设y∈D~, (x→y)→0∈D~, 则y~0, (x→y)→0~0. 由~是同余关系,x~x,0~0得
y→0~0→0=1,x→((x→y)→0)~x→0,
由(S3)得(x→y)→(x→0)~x→0, 由(S4)得(y→0)→((x→y)→(x→0))=1, 结合y→0~1, 得
(y→0)→((x→y)→(x→0))~1→(x→0),
即x→0~1, 所以(x→0)→0~1→0=0.
又由性质1中4)得x→((x→0)→0)=1, 则x≤(x→0)→0, 从而
(x→0)→0=((x→0)→0)⊕x~0⊕x=x,
所以(x→0)→0~x, 进而由(x→0)→0~0得x~0, 即x∈D~. 故D~是M上的蕴涵理想.
引理1设M是SWBR0-代数,D是M的一个蕴涵理想, 定义x~Dy当且仅当(x→y)→0∈D, (y→x)→0∈D(x,y∈M), 则~D是M上的等价关系.
证明: ∀x,y,z∈M, 分下列几种情况证明:
1) 由性质1中3)和(S7)得(x→x)→0=0∈D, 则x~Dx.
2) 若x~Dy, 则(x→y)→0∈D, (y→x)→0∈D, 即(y→x)→0∈D, (x→y)→0∈D, 故y~Dx.
3) 若x~Dy,y~Dz, 则(x→y)→0∈D, (y→x)→0∈D, 且(y→z)→0∈D, (z→y)→0∈D. 由(S3),(S4)得(x→y)→((y→z)→(x→z))=1, 则
((x→y)→((y→z)→(x→z)))→((((y→z)→(x→z))→0)→((x→y)→0))=1.
结合(S7)得
(((y→z)→(x→z))→0)→((x→y)→0)=1,
则
((((y→z)→(x→z))→0)→((x→y)→0))→0=1→0=0∈D.
又(x→y)→0∈D, 则((y→z)→(x→z))→0∈D.
令A=(y→z)→(x→z),B=(x→z)→0,C=(y→z)→0, 则A→0∈D,C∈D. 又由(S3),(S4)得
A→(B→C)=1, (A→(B→C))→(((B→C)→0)→(A→0))=1,
从而由(S7)得((B→C)→0)→(A→0)=1, 于是
(((B→C)→0)→(A→0))→0=1→0=0∈D.
又A→0∈D, 所以(B→C)→0∈D. 因为C∈D, 所以B∈D, 即(x→z)→0∈D.
同理可证(z→x)→0∈D. 故x~Dz. 所以~D是M上的等价关系.
定理2设M是SWBR0-代数,D是M的一个蕴涵理想, 定义x~Dy当且仅当(x→y)→0∈D,(y→x)→0∈D(x,y∈M), 则~D是M上的同余关系.
证明: 由引理1知, ~D是M上的等价关系. 只需证明~D被⊕,→所保持.
1) 设x~Dy,z~Dw, 下证x⊕z~Dy⊕w.
因为x~Dy, 则(x→y)→0∈D, (y→x)→0∈D. 又由命题1中3)得(x→(y⊕z))→0≤(x→y)→0, 由命题2中1)知, (x→(y⊕z))→0∈D. 因为
故由性质1中5)知, (((x→(y⊕z))→0)→0)→0∈D, 即((x⊕z)→(y⊕z))→0∈D. 同理可证((y⊕z)→(x⊕z))→0∈D. 则x⊕z~Dy⊕z.
因为z~Dw,y~Dy, 同理可得z⊕y~Dw⊕y. 又z⊕y=y⊕z,w⊕y=y⊕w, 所以由~D的传递性知,
x⊕z~Dy⊕z~Dz⊕y~Dw⊕y~Dy⊕w,
即x⊕z~Dy⊕w.
2) 设x~Dy,z~Dw, 下证x→z~Dy→w.
因为x~Dy,z~Dz, 所以(x→y)→0∈D, (y→x)→0∈D. 由引理1的证明3)得
((y→z)→(x→z))→0∈D.
同理可得((x→z)→(y→z))→0∈D. 则x→z~Dy→z. 又z~Dw,y~Dy, 类似可证y→z~Dy→w. 由~D的传递性可知,x→z~Dy→w.
综上可知, ~D是M上的同余关系.
3 基于蕴涵理想的SWBR0-代数的商代数
设D是SWBR0-代数的一个蕴涵理想, 定义x~Dy当且仅当(x→y)→0∈D, (y→x)→0∈D, 由引理1知, ~D是M上的等价关系. 设x所在的等价类为[x](x∈M), 全体等价类记为M/~D. 由定理2知, ~D是M上的关于运算→,⊕的同余关系, 从而可得到M/~D上的诱导运算→,⊕. 它们的定义分别为
→: (M/~D)2→M/~D: [x]→[y]=[x→y] ([x],[y]∈M/~D);
⊕: (M/~D)2→M/~D: [x]⊕[y]=[x⊕y] ([x],[y]∈M/~D),
(M/~D,⊕,→,[0],[1])称为M关于~D的商代数, 记作M/D.
定理3设D是SWBR0-代数的一个蕴涵理想, 则M/D是SWBR0-代数.
证明: ∀[a],[b],[c]∈M/D, 有:
1) [a]⊕[0]=[a⊕0]=[a];
2) [a]⊕[b]=[a⊕b]=[b⊕a]=[b]⊕[a], 即[a]⊕[b]=[b]⊕[a];
3) 因为[a]→([b]→[c])=[a]→[b→c]=[a→(b→c)]=[b→(a→c)],
[b]→([a]→[c])=[b]→[a→c]=[b→(a→c)],
所以[a]→([b]→[c])=[b]→([a]→[c]);
4) ([b]→[c])→ (([a]→[b])→([a]→[c]))=[b→c]→([a→b]→[a→c])=
[b→c]→[(a→b)→(a→c)]=[(b→c)→((a→b)→(a→c))]=[1];
5) [a]→([a]⊕[b])=[a]→[a⊕b]=[a→(a⊕b)]=[1];
6) ([a]⊕[b])→[c]= [(a⊕b)→c]=[(((a→c)→0)⊕((b→c)→0))→0]=
([(a→c)→0]⊕[(b→c)→0])→[0]=
(([a→c]→[0])⊕([b→c]→[0]))→[0]=
((([a]→[c])→[0])⊕(([b]→[c])→[0]))→[0];
7) [1]→[a]=[1→a]=[a];
8) 设[a]→[b]=[1], [b]→[a]=[1], 则[a→b]=[b→a]=[1], 即a→b~D1,b→a~D1. 因此(a→b)→0~D1→0=0, 所以(((a→b)→0)→0)→0∈D. 结合性质1中5)知, (a→b)→0∈D.
同理可证(b→a)→0∈D. 所以a~Db, 即[a]=[b].
综上,M/D是一个SWBR0-代数.
定理4设M是SWBR0-代数, 则典型映射p:M→M/D是满同态.
证明: 典型映射[4]p:M→M/D的定义为p(x)=[x],x∈M. 因为p(M)=[M]=M/~D, 所以p是满射. ∀x,y∈M, 有
p(x→y)=[x→y]=[x]→[y]=p(x)→p(y),
p(x⊕y)=[x⊕y]=[x]⊕[y]=p(x)⊕p(y),
故p是M→M/D的满同态.
定理5设Y,Z是SWBR0-代数,f是Y到Z的代数同态,D,D′分别是Y,Z的蕴涵理想, 若f(D)⊆D′, 则存在代数同态f*:Y/D→Z/D′.
证明: 定义f*:Y/D→Z/D′. ∀y∈Y,f*([y])=[f(y)].
下面说明f*定义的合理性. ∀y1,y2∈Y, 若[y1]=[y2], 即y1~Dy2, 则(y1→y2)→0∈D, (y2→y1)→0∈D, 从而有
f((y1→y2)→0)∈f(D)⊆D′,f((y2→y1)→0)∈f(D)⊆D′,
于是
(f(y1)→f(y2))→0∈D′, (f(y2)→f(y1))→0∈D′,
所以f(y1)~D′f(y2), 即[f(y1)]=[f(y2)]. 故f*的定义是合理的.
∀y1,y2∈Y, 有
f*([y1]→[y2])=f*([y1→y2])=[f(y1→y2)]=[f(y1)]→[f(y2)]=f*([y1])→f*([y2]),
f*([y1]⊕[y2])=f*([y1⊕y2])=[f(y1⊕y2)]=[f(y1)]⊕[f(y2)]=f*([y1])⊕f*([y2]),
则f*是Y/D→Z/D′的同态.
定理6设(X,⊕,→,0,1), (Y,⊕′,→′,0,1)是SWBR0-代数,f:X到Y的满同态, 则Kerf={xf(x)=0,x∈X}是X的蕴涵理想, 且X/Kerf≅Y.
证明: 因为f(0)=0, 所以0∈Kerf. 若y∈Kerf, (x→y)→0∈Kerf, 则f(y)=0,f((x→y)→0)=0, 从而有(f(x)→f(y))→f(0)=0, 即(f(x)→0)→0=0, 又f(x)≤(f(x)→0)→0, 于是f(x)≤0, 因为f(x)≥0, 所以f(x)=0, 即x∈Kerf, 故Kerf是X的蕴涵理想.
设g是X→X/Kerf的映射, 由定理4知,g是满同态. 定义h:X/Kerf→Y, ∀x∈X,h([x])=f(x). ∀x,y∈X,x~y当且仅当(x→y)→0∈Kerf, (y→x)→0∈Kerf, 当且仅当(f(x)→f(y))→0=0, (f(y)→f(x))→0=0. 因此x~y当且仅当f(x)~f(y). 从而h的定义是合理的.
因为f是满射, 所以h是满射. ∀x,y∈X, 若f(x)=f(y), 则f(x)~f(y), 从而x~y, 即[x]=[y], 则f是单射, 所以f是双射.
∀x,y∈X, 有
h([x]→[y])=h[x→y]=f(x→y)=f(x)→′f(y)=h([x])→′h([y]),
h([x]⊕[y])=h[x⊕y]=f(x⊕y)=f(x)⊕′f(y)=h([x])⊕′h([y]),
所以f是同构. 故X/Kerf≅Y.
[1] WU Wang-ming. Fuzzy Implication Algebras [J]. Fuzzy Systems and Mathematics, 1990, 4(1): 56-64. (吴望名. Fuzzy蕴涵代数 [J]. 模糊系统与数学, 1990, 4(1): 56-64.)
[2] XU Yang. Lattice Implication Algebras [J]. Journal of Southwest Jiaotong University, 1993, 28(1): 20-27. (徐扬. 格蕴涵代数 [J]. 西南交通大学学报, 1993, 28(1): 20-27.)
[3] WANG Guo-jun. A Kind of Formal Deduction Systems of Fuzzy Propositional Calculation [J]. Chinese Science Bulletin, 1997, 42(10): 1041-1045. (王国俊. 模糊命题演算的一种形式演绎系统 [J]. 科学通报, 1997, 42(10): 1041-1045.)
[4] 王国俊. 数理逻辑引论与归结原理 [M]. 2版. 北京: 科学出版社, 2006.
[5] 王国俊. 非经典数理逻辑与近似推理 [M]. 2版. 北京: 科学出版社, 2008.
[7] Esteva F, Godo L. Monoidalt-Norm Based Logic towards a Logic for Left Continuoust-Norm [J]. Fuzzy Sets and Systems, 2001, 124(3): 271-288.
[8] WU Hong-bo. Basis R0-Algebra and BasisL*Systems [J]. Advances in Mathematics, 2003, 32(5): 565-576. (吴洪博. 基础R0-代数与基础L*系统 [J]. 数学进展, 2003, 32(5): 565-576.)
[9] WU Hong-bo, WANG Zhao-hai. The Non-ordered Form of BR0-Algebras and Properties of WBR0-Algebras [J]. Chinese Journal of Engineering Mathematics, 2009, 26(3): 456-460. (吴洪博, 王昭海. BR0-代数的无序表示形式及WBR0-代数的性质 [J]. 工程数学学报, 2009, 26(3): 456-460.)
[10] CHENG Guo-sheng. The Filters and the Ideals in R0-Algebras [J]. Fuzzy Systems and Mathematics, 2001, 15(1): 58-61. (程国胜. R0-代数中的滤子与理想 [J]. 模糊系统与数学, 2001, 15(1): 58-61.)
[11] ZHOU Jian-ren, WU Hong-bo. The Regularness of WBR0-Algebras and Relationship with Other Logic Algebras [J]. Journal of Shandong University: Natural Science, 2012, 47(2): 86-92. (周建仁, 吴洪博. WBR0-代数的正则性及与其他逻辑代数的关系 [J]. 山东大学学报: 理学版, 2012, 47(2): 86-92.)
[12] SUN Shao-quan, GU Wen-xiang. Fuzzy Factor Algebras and the Fundamental Theorem of Homomorphisms [J]. Journal of Northeast University: Natural Science Edition, 2002, 34(2): 22-25. (孙绍权, 谷文祥. Fuzzy商代数与同态基本定理 [J]. 东北师大学报: 自然科学版, 2002, 34(2): 22-25.)
[13] WANG Zhi-ming, WU Hong-bo. An Construction and Properties of WBR0-Algebra [J]. Fuzzy Systems and Mathematics, 2011, 25(4): 55-61. (王志明, 吴洪博. WBR0-代数的构建与性质 [J]. 模糊系统与数学, 2011, 25(4): 55-61.)

