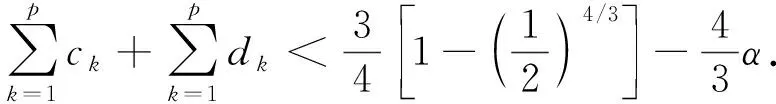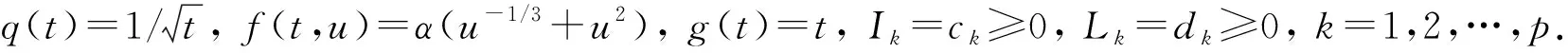脉冲微分方程非局部奇异边值问题
苗春梅,葛渭高
(1. 长春大学 理学院,长春 130022;2. 吉林大学 数学学院,长春 130012;3. 北京理工大学 数学学院,北京 100081)
0 引 言
脉冲微分方程应用广泛,关于其稳定性、 振动性、 边值问题等研究目前已有许多结果[1-12]. 但关于脉冲微分方程非局部奇异边值问题的研究结果较少,多数都是两点边值问题[13-16].
Dai等[14]运用上下解方法研究了如下奇异Emden-Fowler边值问题:
其中:λ,m,a,b,c,d≥0;p(t),q(t)在t=0和t=1处具有奇性;非线性项f(t,x)=p(t)xλ+q(t)x-m在x=0处具有奇性,但该问题中的非线性项是具体的多项式函数,不具有一般性.
在非局部边值问题中,带有积分边界条件的问题在热传导问题[17]、 水力问题[18]和半导体问题[19]中应用广泛,两点边界条件实质上是积分边界条件的特殊情形.
基于此,本文研究如下带有积分边界条件的脉冲微分方程奇异边值问题:
(1)
其中: 0 假设如下条件成立: PC[J]={u:J→R|u(t)在J0上连续且u(tk-0)=u(tk),u(tk+0)(k=1,2,…,p)存在}; PC1[J]={u:J→R|u′(t)在J0上连续且u′(tk-0)=u′(tk),u′(tk+0)(k=1,2,…,p)存在}. 定义1如果函数u∈PC1[J]∩C2[J′]满足式(1)且u(t)>0,t∈(0,1),则称u为边值问题(1)的正解. 定义2[4]如果对任意的u∈S,ε>0,存在δ>0,使得s,t∈Jk(k=1,2,…,p)且|s-t|<δ,有|u(s)-u(t)|<ε,则称集合S⊂PC[J]是拟等度连续的. 定义3[4]如果对任意的u∈S,ε>0,存在δ>0,使得s,t∈Jk(k=1,2,…,p)且|s-t|<δ,有|u(s)-u(t)|<ε和|u′(s)-u′(t)|<ε,则称集合S⊂PC1[J]是拟等度连续的. 引理1[4]集合S⊂PC[J](S⊂PC1[J])在PC[J](PC1[J])上相对紧当且仅当S是有界的且拟等度连续. 引理2对常数ak,bk≥0(k=1,2,…,p)和y∈L1[J],边值问题 (2) 存在唯一解: 证明: 由式(2)知 u″(t)=-y(t),t∈J′. (4) (5) 再对式(5)从0到t积分得 (6) 将式(6)两边同时乘以g(t),再从0到1积分,由边界条件可得 结合式(6)可得 从而,对任意的t∈[0,1],有 证毕. 为研究奇异边值问题(1)解的存在性,先考虑如下边值问题: (7) 定义算子T:PC[J] →PC[J]为 引理3算子T:PC[J] →PC[J]全连续. 因此,T(B)是一致有界的. 对任意的ε>0,t,s∈Jk(k=0,1,…,p), 引理4假设存在与λ无关的常数R>a≥0,使得对任意的λ∈(0,1),边值问题 (9) 的解u(t)都有‖u‖≠R,则当λ=1时,边值问题(9)至少有一个解u∈PC1[J]∩C2[J′],且‖u‖≤R. 证明: 对任意的λ∈[0,1],u∈PC[J],定义 由引理3知,Nλ:PC[J] →PC[J]全连续. 易证u(t)是边值问题(9)的解当且仅当u是Nλ在PC[J]中的不动点. 令Ω={u∈PC[J]|‖u‖ 引理5如果u(t)是边值问题(7)的解,则: 1)u(t)在Jk(k=0,1,…,p)上是凹的; 2)u′(t)≥ 0,t∈J0,u′(tk-0)≥u′(tk+0)≥0,Δu(tk)≥0,k=1,2,…,p; 3)u(t)≥a,t∈[0,1]. 定理1设(H1)成立,再假设下列条件成立,则边值问题(1)至少存在一个正解: (H3) 对任意的l>0,存在函数ψl: [0,1] → (0,∞),使得f(t,u)≥ψl(t),(t,u)∈J′×(0,l]; 证明: 由(H4)知,存在M>0和0<ε<(1-σ)M,使得 (11) (12) 有解. 为了证明对任意的m∈N0,边值问题(12)都有解,先考虑边值问题: (13) 其中: 下面应用引理4证明边值问题(13)有解. 为此,先考虑如下一族边值问题: (14) 由(H2)知,对任意的x∈J′, -u″(x)=λq(x)f*(x,u(x))=λq(x)f(x,u(x))≤q(x)[f1(u(x))+f2(u(x))], (15) 对式(15)从t(t∈J0)到1积分并由u′(t)的单调性可得 (16) 将式(16)两边同时除以f1(u(t)),再由0到1积分可得 进而有 结合式(11)可得‖u‖=u(1)≠M. 又由引理4知,对任意固定的m∈N0,边值问题(13)至少有一个解um∈PC1[J]∩C2[J′],满足‖um‖≤M. 由引理5知,um(t)≥1/m>0,从而 因此um(t)也是边值问题(12)的解. 下面将获得um(t)(∀m∈N0)的拟下界,即存在常数L>0,L0≥0(与m无关),使得 um(t)≥Lt+L0,t∈J. (17) 由于 0<1/m≤um(t)≤M,t∈J. (18) 故由(H3)知,存在连续函数ψM: [0,1] → (0,∞),使得:f(t,um(t))≥ψM(t),t∈J′. 又由引理2知, 最后证明{um(t)}m∈N0在J上是一致有界且拟等度连续的. 由式(18)知{um(t)}m∈N0在J上是一致有界的. 下面证明其在J上是拟等度连续的. 因为um(t)是式(12)的解,因此对x∈J′,有 -um″(x)=q(x)f(x,um(x))≤q(x)[f1(um(x))+f2(um(x))], (20) 将式(20)从t(t∈J0)到1积分并由u′(t)的单调性可得 (21) 因此{um(t)}m∈N0在J上是拟等度连续的. 又由于 在式(22)中,令m→ ∞,m∈N*,由Lebesgue控制收敛定理可得 因此u(t)是边值问题(1)的正解,且u(t)≥Lt+L0,t∈J,‖u‖≤M. 证毕. 例1考虑边值问题: (23) 边值问题(23)至少有一个正解. 从而(H4)成立,因此,由定理1可知,边值问题(23)至少存在一个正解. 证毕. [1] Bainov D D,Simeonov P S. Systems with Impulse Effect: Stability,Theory and Applications [M]. Chichester: Ellis Horwood Ltd,1989. [2] Lakshmikantham V,Bainov D D,Simeonov P S. Theory of Impulsive Differential Equations [M]. Singapore: World Scientific,1989. [3] Bainov D D,Simeonov P S. Impulsive Differential Equations: Periodic Solutions and Applications [M]. Harlow: Longman,1993. [4] Samoilenko A M,Perestyuk N A. Impulsive Differential Equations [M]. Singapore: World Scientific,1995. [5] FENG Mei-qiang,PANG Hui-hui. A Class of Three-Point Boundary-Value Problems for Second-Order Impulsive Integro-Differential Equations in Banach Spaces [J]. Nonlinear Anal: Theor Meth Appl,2009,70(1): 64-82. [6] Jankowski T. Positive Solutions of Three-Point Boundary Value Problems for Second Order Impulsive Differential Equations with Advanced Arguments [J]. Appl Math Comput,2008,197(1): 179-189. [7] Jankowski T. Positive Solutions to Second Order Four-Point Boundary Value Problems for Impulsive Differential Equations [J]. Appl Math Comput,2008,202(2): 550-561. [8] FENG Mei-qiang,XIE Dong-xiu. Multiple Positive Solutions of Multi-point Boundary Value Problem for Second-Order Impulsive Differential Equations [J]. J Comput Appl Math,2009,223(1): 438-448. [9] LIU Bing,YU Jian-she. Existence of Solution form-Point Boundary Value Problems of Second-Order Differential Systems with Impulses [J]. Appl Math Comput,2002,125(2/3): 155-175. [10] ZHANG Xue-mei,GE Wei-gao. Impulsive Boundary Value Problems Involving the One-Dimensionalp-Laplacian [J]. Nonlinear Anal: Theor Meth Appl,2009,70(4): 1692-1701. [11] FENG Mei-qiang,DU Bo,GE Wei-gao. Impulsive Boundary Value Problems with Integral Boundary Conditions and One-Dimensionalp-Laplacian [J]. Nonlinear Anal: Theor Meth Appl,2009,70(9): 3119-3126. [12] TIAN Yu,JI De-hong,GE Wei-gao. Existence and Nonexistence Results of Impulsive First-Order Problem with Integral Boundary Condition [J]. Nonlinear Anal: Theor Meth Appl,2009,71(3): 1250-1262. [13] Agarwal R P,Franco D,O’Regan D. Singular Boundary Value Problems for First and Second Order Impulsive Differential Equations [J]. Aequationes Math,2005,69(1/2): 83-96. [14] DAI Li-mei,LI Hong-yu. Positive Solutions of Singular Emden-Fowler Boundary Value Problem with Negative Exponent and Multiple Impulses [J]. Nonlinear Anal: Theor Meth Appl,2009,70(10): 3682-3695. [15] LI Qiu-yue,CONG Fu-zhong,JIANG Da-qing. Multiplicity of Positive Solutions to Second Order Neumann Boundary Value Problems with Impulse Actions [J]. Appl Math Comput,2008,206(2): 810-817. [16] ZU Li,JIANG Da-qing,O’Regan D. Existence Theory for Multiple Solutions to Semipositone Dirichlet Boundary Value Problems with Singular Dependent Nonlinearities for Second-Order Impulsive Differential Equations [J]. Appl Math Comput,2008,195(1): 240-255. [17] Cannon J R. The Solution of the Heat Equation Subject to the Specification of Energy [J]. Quart Appl Math,1963,21(2): 155-160. [18] Chegis R Y. Numerical Solution of a Heat Conduction Problem with an Integral Boundary Condition [J]. Litovsk Mat Sb,1984,24: 209-215. [19] Ionkin N I. Solution of a Boundary Value Problem in Heat Conduction Theory with Nonlocal Boundary Conditions [J]. Diff Equ,1977,13: 294-304.
1 预备知识

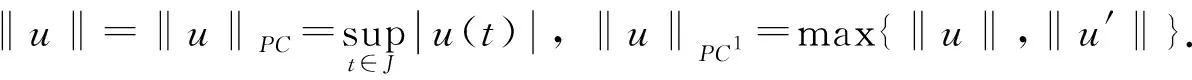
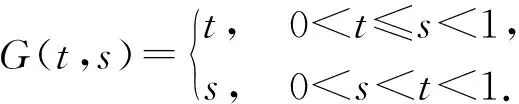

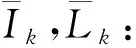


2 主要结果



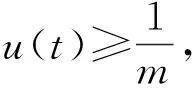


3 应用实例