一维光子晶体中的光场特性
王 婧,吴向尧,刘晓静,巴 诺,张斯淇,李 宏,郭义庆,尹新国
(1.吉林师范大学 物理学院,吉林 四平136000;2.中国科学院 高能物理研究所,北京 100049;3.淮北师范大学 物理学院,安徽 淮北 235000)
Yablonovitch[1]和John[2]在讨论周期性电介质结构对材料中光传播行为的影响时,分别提出了光子晶体的概念.光子晶体是按照晶体的对称性制备的周期性介电结构,其电磁模式像晶体中的电子一样具有能带结构.当光的频率在禁带中时,光的传播被禁止[3].使其在光子晶体光纤、 光子晶体波导、 全向反射镜、 光子晶体滤波器和光子晶体偏振器等方面应用广泛[4-10].目前,光子晶体研究主要集中在讨论垂直入射光在光子晶体的透射率及色散关系.本文在此基础上,给出任意角度入射光在光子晶体中的透射率、 反射率及内部场强分布公式,并结合透射率和反射率研究光在一维光子晶体内的场强分布,讨论入射光的角频率和角度及光子晶体周期数和光学厚度对场强分布的影响.
1 任意角度入射光在一维光子晶体中的传输矩阵、 透射率及反射率
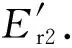

图1 任意角度入射光在一维光子晶体介质中的传播Fig.1 Transmissivity of incidence light at arbitrary incidence angle in photon crystals
由电场和磁场的边值关系可知,界面Ⅰ两侧的电场强度和磁场强度在切向方向上的分量是连续的,即
(1)
界面Ⅱ两侧的电场强度和磁场强度可表示为
(2)
电场强度Et1和Ei2分别为
(3)
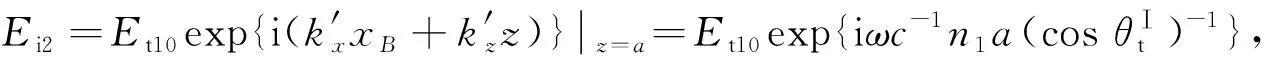
(4)
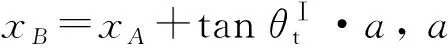
式(4)可变为
Ei2=Et1eiδa,
(5)
同理
(6)
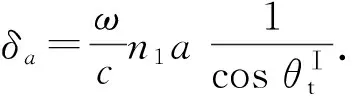
(7)
其中:ε0为真空介电常数;μ0为真空介质磁导率.
式(7)可变为
(8)
其中
(9)

(10)
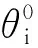
(11)

(12)

从而可得一个周期的传输矩阵为
(13)
对于第N个周期,其电场强度EN,EN+1和磁场强度HN,HN+1满足如下关系式:
(14)
由式(14)可得任意入射角的光在N个周期光子晶体中的特征方程,即传输矩阵:
(15)
其中M=M1M2…MN=MaMbMaMb…MaMb.
根据第一个界面和第N+1个界面上的电磁分量方程,可求出任意角度入射光在一维光子晶体中传播的透射率和反射率,分别为:
透射系数
(16)
透射率
T=t·t*;
(17)
反射系数
(18)
反射率
R=r·r*.
(19)
2 任意角度入射光在一维光子晶体中的场强分布
任意角度入射光在一维光子晶体中的场强分布如图2所示.由任意角度入射光在一维光子晶体中的传播矩阵可得
(20)
其中: ΔzN为第N个周期内的传播距离;E0和H0分别为入射电场和磁场强度;EN(d1+d2+…+dN-1+ΔzN)和HN(d1+d2+…+dN-1+ΔzN)分别为光在第N个周期内的电场强度和磁场强度.通过变换可得:
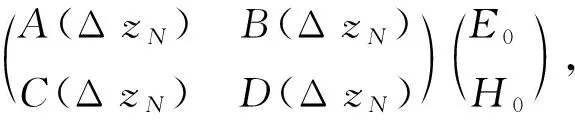
(21)
E0=Ei1+Er1=(1+r)Ei1,
(22)

(23)
由式(21)~(23)即可得任意角度入射光在一维光子晶体中的电场分布为
(24)
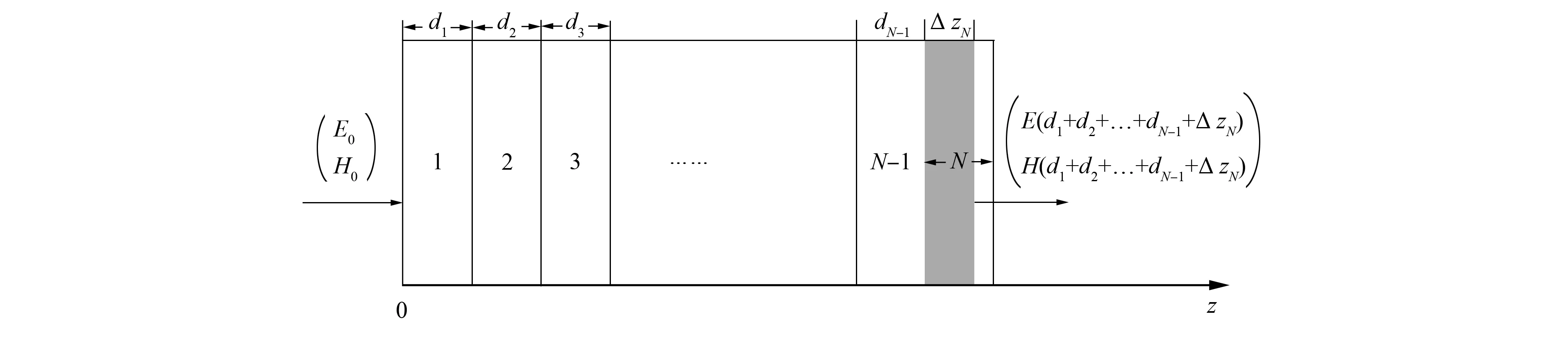
图2 任意角度入射光在一维光子晶体中的场强分布Fig.2 Electron field distribution of incident light in 1D photon crystals
3 数值分析
本文研究的光子晶体分别由Si和Al2O3作为介质层A和B,折射率分别为na=3.42,nb=1.766,周期数N=8,即结构为(AB)8,λ0=679 nm,对应角频率ω0=2πc/λ0,其中c为真空中光速,光学厚度naa=nbb=λ0/4,其中a和b分别为介质层A和B的厚度.
由式(16)~(19)可得垂直入射光在(AB)8结构的一维光子晶体中反射率及透射率随角频率变化的曲线,如图3所示,其中: 横轴为入射光角频率与基频ω0的比值;纵轴为不同角频率的光在一维光子晶体中传播时对应的反射率及透射率.由图3(A)可见: 当横轴ω/ω0为奇数时,其对应的反射率近似为1(ω=ω0,R=0.999 897 795 201 119 9;ω=3ω0,R=0.999 897 795 201 119 9);当横轴ω/ω0为偶数时,其对应的反射率近似为0(ω=2ω0,R=4.493 215 313 876 917×10-30;ω=4ω0,R=1.797 286 125 550 766 8×10-29).由图3(B)可见,当横轴ω/ω0分别为奇数和偶数时,其对应的透射率分别近似为0和1.

图3 垂直入射光在一维光子晶体中随频率变化的反射率(A)和透射率(B)曲线Fig.3 Reflectivity curve (A) and transmissivity curve (B) of vertically incident light changed with angle frequency in photon crystals
角频率分别为ω0,3ω0,2ω0,4ω0的垂直入射光在一维光子晶体中的场强分布曲线如图4所示,其中横轴为光在一维光子晶体中的传播位置,纵轴为其所在位置对应场强与入射场强比值的模方.由图4可见: 当入射光角频率为基频奇数倍时,其场强较弱,与入射场强比值的最大值小于0.35,场强随入射光位置的增大逐渐减弱,最终趋为0;当入射光角频率为基频偶数倍时,其场强较强,与入射场强比值的最大值近似为1,场强随入射光位置的增大呈周期性分布;透射率越大,相应的场强越大;每个周期内波峰数随入射光角频率的增大而增加,且波峰数与其入射光对应的基频倍数相同,但场强分布的总趋势保持不变.

图4 角频率分别为ω0(A),3ω0(B),2ω0(C),4ω0(D)的垂直入射光在(AB)8结构一维光子晶体中的场强分布曲线Fig.4 Electron field distribution curves of incidence light in photon crystals of (AB)8 structure with ω0 (A),3ω0 (B),2ω0 (C),4ω0 (D)
角频率分别为2.5ω0,3.5ω0,4.5ω0,5.5ω0的垂直入射光在一维光子晶体中的场强分布曲线如图5所示.由图5可见,每个周期(仅标示了(D)中一个周期分界线)内波峰数随入射光角频率的增大而增加,且每个周期内完整波峰数与基频倍数中的整数相同.即每个周期内完整波峰数分别为2,3,4,5.

图5 角频率分别为2.5ω0(A),3.5ω0(B),4.5ω0(C),5.5ω0(D)的入射光 在(AB)8结构一维光子晶体中的场强分布曲线Fig.5 Electron field distribution curves of incidence light in photon crystals of (AB)8 structure with 2.5ω0 (A),3.5ω0 (B),4.5ω0 (C),5.5ω0 (D)
周期数对场强分布的影响分别如图6和图7所示.由图6可见,当入射光角频率均为2ω0或3ω0,周期数N分别为8和12时,在相同周期处的场强分布完全相同,增大光子晶体周期数不影响场强分布.即角频率为整数倍基频的入射光,保持其他参数不变,改变其传播的光子晶体周期数不影响光的场强分布.这是由于当入射光角频率为整数倍基频时,其相应反射率近似为0或1,改变光子晶体周期数,其反射率变化极小,对场强分布影响较弱所致.

图6 角频率均为2ω0(A),(B)或3ω0(C),(D) 的入射光在(AB)8 和(AB)12 结构一维光子晶体中的场强分布曲线Fig.6 Electron field distribution curves of incidence light with angle frequency 2ω0 (A),(B) or 3ω0 (C),(D) of (AB)8 and (AB)12 structure photon crystals
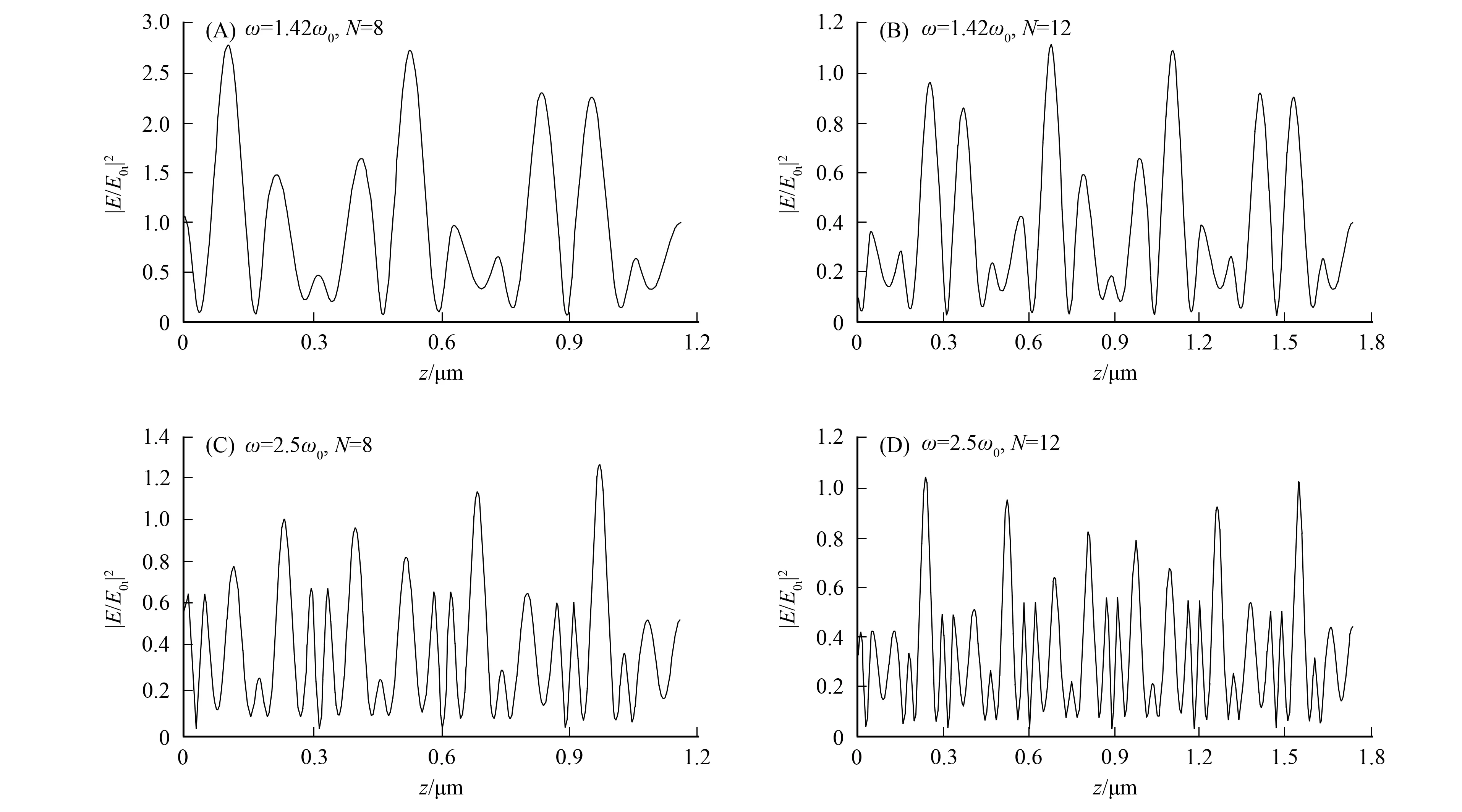
图7 角频率均为1.42ω0(A),(B)或2.5ω0(C),(D) 的入射光在(AB)8 和(AB)12 结构一维光子晶体中的场强分布曲线Fig.7 Electron field distribution curves of incidence light with 1.42ω0 (A),(B) or 2.5ω0 (C),(D) of (AB)8 and (AB)12 structure photon crystals
由图7可见,当入射光角频率均为1.42ω0或2.5ω0,周期数N分别为8和12时,其场强分布随周期数的增大而降低,即角频率为非整数倍基频的入射光,增大其传播的光子晶体周期数,其相应的场强分布减弱.
角频率为2ω0的垂直入射光在光学厚度nad分别为λ0/4,λ0/2和λ0光子晶体中的场强分布曲线如图8所示.由图8可见: 每个周期内波峰数随光子晶体光学厚度的等比增大而等比增加,其公比与光学厚度增加的公比相等;改变光子晶体光学厚度并不改变其场强呈周期性分布的性质.

图8 角频率为2ω0的垂直入射光在光学厚度分别为λ0/4(A),λ0/2(B) 和λ0(C)的(AB)8结构一维光子晶体中的场强分布曲线Fig.8 Electron field distribution curves of incidence light in photon crystals of (AB)8 structure with optical thickness λ0/4 (A),λ0/2 (B) and λ0 (C),angle frequency 2ω0
综上,本文可得如下结论:
1) 当入射光角频率为基频奇数倍时,其透射率近似为零,场强较弱,与入射光场强比值的最大值小于0.35,场强随入射光位置的增大逐渐减弱,最终趋近为0,每个周期内波峰数随入射光角频率的增大而增加,与其入射光频率对应的基频倍数相同;
2) 当入射光角频率为基频偶数倍时,其透射率近似为1,场强较强,与入射光场强比值的最大值为1,且场强分布呈周期性分布,每个周期内波峰数随入射光角频率的增大而增加,与其入射光频率对应的基频倍数相同;
3) 当入射光角频率为非整数倍基频时,每个周期内波峰数随角频率的增大而增加,且每个周期内完整波峰数与基频倍数中的整数相同;
4) 当入射光角频率为整数倍基频时,其反射率近似为0或1,改变光子晶体周期数,其反射率变化极小,因此对场强分布的影响较弱;
5) 当入射光角频率为非整数倍基频时,增大传播的光子晶体周期数,其相应的场强分布减弱;
6) 每个周期内波峰数随光子晶体光学厚度的等比增大而等比增加,其公比与光学厚度增加的公比相等;
7) 光在光子晶体内部场强随入射角度的减小而增强.
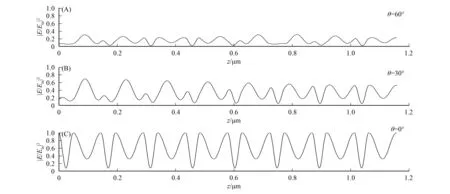
图9 角频率为2ω0,入射角分别为60°(A),30°(B)和0°(C) 的光在(AB)8结构一维光子晶体中的场强分布曲线Fig.9 Electron field distribution curves of incidence light in photon crystals of (AB)8 structure with incidence angle 60° (A),30° (B) and 0° (C),angle frequency 2ω0
[1] Yablonovitch E.Inhibited Spontaneous Emission in Solid-State Physics and Electronics [J].Phys Rev Lett,1987,58(20): 2059-2062.
[2] John S.Strong Localization of Photons in Certain Disordered Dielectric Superlattices [J].Phys Rev Lett,1987,58(23): 2486-2489.
[3] WAN Jun,ZHANG Chun,WANG Ling-jun.Photonic Crystals and Their Applications [J].Physics,1999,28(7): 393-398.(万钧,张春,王领军.光子晶体及其应用 [J].物理,1999,28(7): 393-398.)
[4] FAN Shan-hui,Villeneuve P R,Joanhopoulos J D,et al.High Extraction Efficiency of Spontaneous Emission from Slabs of Photonic Crystals [J].Phys Rev Lett,1997,78(17): 3294-3297.
[5] GUO Shu-qin,LIU Yin-ping,ZHU Guang-xin.Photonic Crystal Fiber with Snowflake Shape Crystal Core [J].Acta Photonica Sinica,2007,36(7): 1207-1210.(郭淑琴,刘印平,朱广信.雪花形晶芯光子晶体光纤 [J].光子学报,2007,36(7): 1207-1210.)
[6] Kenji Ishizaki,Susumu Noda.Manipulation of Photons at the Surface of Three-Dimensional Photonic Crystals [J].Nature,2009,460: 367-370.
[7] FANG Liang,ZHAO Jian-lin,GAN Xue-tao,et al.Generation and Control of Supercontinuum in Photonic Crystal Fibers with Two-Zero Dispersion Wavelengths [J].Acta Photonica Sinica,2010,39(11): 1921-1927.(方亮,赵健林,甘雪涛,等.双零色散光子晶体光纤中超连续谱的产生及控制 [J].光子学报,2010,39(11): 1921-1927.)
[8] WANG Hui,LI Yong-ping.An Eigen Matrix Method for Obtaining the Band Structure of Photonic Crystals [J].Acta Physica Sinica,2001,50(11): 2172-2178.(王辉,李永平.用特征矩阵法计算光子晶体的带隙结构 [J].物理学报,2001,50(11): 2172-2178.)
[9] John S.Photonics: Light Control at Will [J].Nature,2009,460: 337.
[10] Russell P.Photonic-Crystal Fibers [J].Science,2003,299: 358-362.

