基于顺序多尺度的智能规划问题模型及其求解方法
刘晓峰,李 欣,曾志勇
(1.吉林省教育学院 综合部,长春 130022;2.东北师范大学 计算机科学与信息技术学院,长春 130117)
在智能规划问题中,用规划尺度(plan metric)描述衡量规划解的质量.如“能量消耗最少”是一个尺度[1-3],根据该尺度,能量消耗为50单位的规划解优于能量消耗为60单位的规划解.带有规划尺度的问题要求规划算法在多个可行规划中找到较优甚至最优的规划解.一个尺度M为任一规划解π隐式定义了一个尺度值计算函数CM(通常CM(π)∈)和该函数值域上的全序关系<,使规划算法能比较多个规划解的优劣.然而,当规划问题存在多个尺度时,衡量规划解的优劣存在困难.假设存在两个尺度M1和M2,两个规划解π1和π2具有如下特征:
CM1(π1) Fox等[2]将多个尺度分别加权、 线性组合形成一个混合尺度解决了π1和π2的优劣性问题,如 CM3(π)=w1×CM1(π)+w2×CM2(π). 但该方法存在两个问题: 1) 线性组合多尺度的意义不明确; 2) 仅能表达尺度的相对重要性,不能表达尺度的绝对重要性. 对于问题1),由于每个尺度所评估的特征实际含义不同,因此将多尺度线性组合的实际含义难理解.此外,在上述线性组合中如果一个尺度的权重大,则表明该尺度值的变化量对混合尺度的影响大,但权重的相对大小无法表示最希望优化的尺度. 为解决上述问题,本文提出一种使用顺序(ordinal order)建模多尺度规划问题的方法将多个尺度按顺序排列表示它们均有顺序性的相对重要性:排列在前的尺度最重要,如对于前述的规划解π1和π2,如果尺度M1排在M2前,则π1优于π2;如果M2排在M1前,则π2优于π1.基于顺序的方法能处理各尺度值计算函数值域不同的情况,从而有更强的建模能力,并能表示尺度的绝对重要性,使规划算法优先根据重要的尺度寻找较优的规划解. 基于本文提出的顺序排序多尺度方法,可以将“规划解长度最短”这个尺度加入到目前带动作代价的规划问题(planning with action costs)[4]和带数值变量的规划问题(planning with numeric variables)[5]中.规划算法将“规划解长度最短”作为默认的尺度能避免多数规划系统面临的当规划解代价为零时陷入宽度优先搜索的问题[6]. 一个规划任务(planning task)表示为T=(V,A,s0,sG),其中:V表示变量的集合,每个变量v具有相应的有限值域Dv;A表示可用的动作集合,一个动作a定义了执行该动作时变量的取值约束及该动作开始执行后对变量取值的改变;s0是一个变量赋值函数,表示初始状态,对任一v∈V满足s0(v)∈Dv;sG表示一个对部分变量有定义的赋值函数,说明在目标状态中变量的期望取值.动作序列π=〈a0,a1,…,an-1〉在状态s上应用的结果是一个状态s′,s′是在s0上依次执行动作a0,a1,…,an-1得到的结果,也可表示为s′=π(s0).如果π(s0)满足目标条件sG,即对于在sG中有定义的任一变量v满足π(s0)(v)=sG(v),则动作序列π称为规划解[7-8]. 一个规划尺度M通常定义在规划任务的某个特征变量上,要求该特征取值最大化或最小化.如在PDDL语言中,“: metric minimizev”表示希望变量v的取值最小.对两个不同的规划解π和π′,如果π(s0)(v)<π′(s0)(v),则π优于π′.在STRIPS规划中,经常关注的一个尺度是“规划解长度(plan length)最小化”.规划解长度表示该规划解所含动作的数目.在时态规划中,一个重要的尺度是“规划解的运行时间最小化”[2]. 定义1一个多尺度规划任务表示为T=(V,A,s0,sG,ME),其中ME表示顺序排列的多个尺度,形式为〈M1,M2,…,Mk〉,每个尺度Mi(i=1,2,…,k)对应一个二元组(CMi(·),<),CMi将每个动作序列π映射到实数集上的一个实数,<表示定义在上的小于关系. 例1规划任务T有顺序尺度〈M1,M2〉,对于两个规划解π和π′,有 CM1(π)=2,CM2(π)=1,CM1(π′)=1,CM2(π′)=3, 则根据定义4,π′优于π.但如果定义混合尺度 CM3(·)= 2×CM1(·)+1×CM2(·), 尽管M1的权重比M2的权重高,却无法依据CM3判断π和π′的优劣. 为了描述顺序多尺度规划任务,本文扩展了智能规划领域定义语言PDDL的语法和语义. 文献[2,9-10]在PDDL的版本2.1(PDDL2.1)中提出了带有规划尺度的规划任务描述形式(参见文献[2]附录A.4).本文在此基础上进行扩展,添加支持顺序多尺度的语法,记为PDDL2.1+OM,语法描述如下: 〈problem〉∷=(define (problem 〈name〉) (: domain 〈name〉) [〈require-def〉]; [〈object declaration〉] 〈init〉 〈goal〉 [〈metric-spec〉] [〈length-spec〉]) 〈object declaration〉∷= (: objects 〈typed list (name)〉) 〈init〉∷=(: init 〈init-el〉_) 〈init-el〉∷=〈literal(name)〉 〈init-el〉∷=: fluents (= 〈f-head〉 〈number〉) 〈goal〉∷=(: goal 〈GD〉) 〈metric-spec〉∷= (: metric 〈optimization〉〈ground-f-exp〉+) 〈optimization〉∷=ordinal-minimize 〈optimization〉∷=ordinal-maximize 〈ground-f-exp〉∷= (〈binary-op〉〈ground-f-exp〉 〈ground-f-exp〉) 〈ground-f-exp〉∷=(-〈ground-f-exp〉) 〈ground-f-exp〉∷=〈number〉 〈ground-f-exp〉∷= (〈function-symbol〉〈name〉_) 〈ground-f-exp〉∷=total-time 〈ground-f-exp〉∷=plan-length 〈ground-f-exp〉∷=〈function-symbol〉. 下面解释PDDL2.1+OM的新语义. 1) 本文将PDDL2.1的语法〈optimization〉∷=minimize和〈optimization〉∷=maximize分别更改为〈optimization〉∷=ordinal-minimize和〈optimization〉∷=ordinal-maximize,表示要求规划算法找到顺序尺度下的最优解.将PDDL2.1的语法〈metric-spec〉∷=(: metric 〈optimization〉〈ground-f-exp〉)改为〈metric-spec〉∷=(: metric〈optimization〉〈ground-f-exp〉+),允许多尺度的顺序声明(PDDL2.1仅支持单个尺度表达式,而PDDL2.1+OM支持多个尺度表达式). 2) 本文语法添加了〈ground-f-exp〉∷=plan-length,其中plan-length表示规划解的长度,即规划解包含的动作数目.该语法允许将STRIPS规划解的长度作为优化尺度. PDDL2.1+OM支持单尺度、 加权组合的混合尺度和顺序多尺度,比PDDL2.1具有更强的建模能力.如果一个具体的规划任务仅关注单个尺度的优化,如规划长度,则可采用形如(: metric ordinal-minimize plan-length)的表达式;如果关注多尺度的加权组合,则可采用形如(: metric ordinal-minimize (+(×2(total-time))(plan-length)))的表达式.如果希望表示total-time尺度绝对比plan-length尺度重要,则可采用形如(: metric ordinal-minimize (total-time)(plan-length))的表达式.因此,有: 结论1任何能由PDDL2.1描述的规划任务均能由PDDL2.1+OM描述. 用PDDL2.1的规划尺度语法描述一个具有相同最优解的顺序多尺度规划任务较难,本文将说明该问题的复杂度是#PSPACE-hard. 定义6假设有语言L描述的规划任务T和语言L′描述的规划任务T′,如果T和T′具有相同的最优解集合,则称T和T′为最优解等价. 定理1用PDDL2.1语言描述顺序多尺度规划任务的复杂度为#PSPACE-hard. 证明:相当于证明任意一个用PDDL2.1+OM描述的顺序多尺度规划任务的描述T,构造一个用PDDL2.1描述的与T等价的描述复杂度为#PSPACE-hard.用DL(T)表示规划任务T在语言L下的描述. 下面给出构造T的PDDL2.1描述DPDDL2.1(T)方法.因为DPDDL2.1(T)除了尺度表达式部分都可以由T的描述DPDDL2.1+OM(T)中复制,所以只需计算DPDDL2.1(T)需要优化的尺度表达式即可.假设T的最优解集合为 (1) 定理1给出了建立DPDDL2.1(T)最优解等价描述DPDDL2.1+OM(T)的一个正确但不完备的算法.本文假设式(1)是一个线性方程,但由式(1)组成的方程组可能无解,从而无法得到期望的DPDDL2.1+OM(T).为了解决该问题,可假设方程(1)是非线性的,相应的求解难度将增大.定理1的另一个问题是其没有根据全部的动作序列π给出混合尺度函数,这将导致那些不是规划解动作序列的尺度值无法预测. 假设1任一尺度Mi对应的函数Cmi对任一动作序列π和π′=cons(π,〈a〉)满足Cmi(π)≤Cmi(π′),则可构造如下Greedy Best-first算法计算顺序多尺度规划任务的满意解. 首先,定义一个函数is_goal(s)判断状态s是否为目标状态,即如果s为目标状态,则该函数返回“真”,否则返回“假”. 算法1多尺度规划求解算法. 初始化: 1) 分别建立一个空的open表和空的closed表,用于记录待扩展的状态和已扩展的状态; 2) 将初始状态s0放入open表,计算s0的顺序尺度值向量(cm1(s0),cm2(s0),…,cmk(s0)). 循环执行如下步骤: 从open表中取出一个状态,令其为s,若is_goal(s)为真,则算法结束,返回解;否则,将s移入closed表,扩展s,生成s的所有子节点,对任意子节点s′,若s′的尺度值劣于s或s′在closed表中,则不将s′放入open表,否则将s′放入open表. 综上所述,本文针对PDDL语言在规划解质量建模方面的缺陷,提出了顺序多尺度的规划问题模型,给出了使用最好优先搜索法求解顺序多尺度规划问题的基本方法,并设计了PDDL2.1+OM语言,证明了PDDL2.1语言若需要具有与PDDL2.1+OM语言等价的建模能力,则需求解一个PSAPACE-hard的困难问题,该命题表明了PDDL2.1+OM语言在建模能力上的优势. [1] McDermott D.PDDL: The Planning Domain Definition Language: Version 1.2 [R].New Haven: Yale Center for Computational Vision and Control,1998. [2] Fox M,Long D.PDDL2.1: An Extension to PDDL for Expressing Temporal Planning Domains [J].J Artif Intell Res,2003,20(1): 61-124. [3] Gerevini A,Long D.Plan Constraints and Preferences in PDDL3 [R].Brescia,Italy: Department of Electronics for Automation,University of Brescia,2005. [4] Keyder K,Geffner H.Soft Goals Can Be Compiled Way [J].J Artif Intell Res,2009,36(1): 547-556. [5] Hoffmann J.The Metric-FF Planning System: Translating “Ignoring Delete Lists” to Numeric State Variables [J].J Artif Intell Res,2003,20(1): 291-341. [6] Helmert M.The Fast Downward Planning System [J].J Artif Intell Res,2006,26(1): 191-246. [7] YIN Ming-hao,ZHOU Jun-ping,SUN Ji-gui.Heuristic Survey Propagation Algorithm for Solving QBF Problem [J].Journal of Software,2011,22(7): 1538-1550.(殷明浩,周俊萍,孙吉贵.求解QBF问题的启发式调查传播算法 [J].软件学报,2011,22(7): 1538-1550.) [8] LI Ying,SUN Ji-gui,WU Xia,et al.Extension Rule Algorithms Based on IMOM and IBOHM Heuristics Strategies [J].Journal of Software,2009,20(6): 1521-1527.(李莹,孙吉贵,吴瑕,等.基于IMOM和IBOHM启发式策略的扩展规则算法 [J].软件学报,2009,20(6): 1521-1527.) [9] YANG Chao,LÜ Shuai,LIU Lei,et al.Research on Action Mutex Encoding Methods in Intelligent Planning [J].Computer Engineering,2011,37(9): 213-215.(杨超,吕帅,刘磊,等.智能规划中的动作互斥编码方式研究 [J].计算机工程,2011,37(9): 213-215.) [10] WEI Wei,OUYANG Dan-tong,LÜ Shuai,et al.Multiobjective Path Planning under Dynamic Uncertain Environment [J].Chinese Journal of Computers,2011,34(5): 836-846.(魏唯,欧阳丹彤,吕帅,等.动态不确定环境下多目标路径规划方法 [J].计算机学报,2011,34(5): 836-846.)1 智能规划的基本概念
2 顺序多尺度规划问题
2.1 规划问题模型
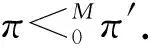
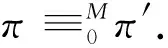


2.2 支持顺序多尺度的PDDL语言扩展
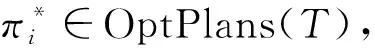

3 顺序多尺度规划问题求解方法

