路基不均匀沉降引起有砟轨道沉降的计算方法

邹春华，周顺华，王长丹，廖 悦

（1.同济大学 道路与交通工程教育部重点实验室，上海201804；2.中铁十三局集团第五工程有限公司，四川 成都610500）

有砟轨道沉降是轨道结构不平顺变形发生、发展的直接原因［1］，而轨道结构不平顺变形是机车车辆产生振动的主要根源，直接影响轮轨间相互作用及列车运行的安全性，平稳性及舒适性.

有砟轨道的沉降主要包括道床沉降和路基沉降.道床沉降的快慢，或者道床的下沉速率，是评估轨道维修工作量及维修周期，比较不同轨道结构承载能力、评估不同轨道结构加强措施效果、比较不同运营条件对轨道的破坏作用等的重要依据［2］.通过国内外学者们几十年共同的努力，道床本身的变形特征及规律已经得到了试验的初步验证［2］.然而，由于铁道线路所处地基的不均匀特性、路基长度或宽度方向上的孔隙率差异、路堤填料的不均匀、在地下水的交替作用下路基土体内含水量反复变化、基床病害引起不均匀沉降等方面的原因，有砟轨道铁路路基不均匀沉降不可避免［3］.路基不均匀沉降一方面致使轨道结构产生差异变形及额外附加应力，可导致结构性损坏；另一方面可使其服务性能的下降，从而对行车安全性和舒适性产生影响［2］.

针对路基不均匀沉降对轨道结构的影响等问题，目前学术界的侧重点仍较多集中在路桥过渡段［4－5］，对一般路基地段的研究很少，且主要是针对无砟轨道结构开展研究工作［6－9］.对于有砟轨道，由于道砟的散粒体物理力学特性的复杂性［10］以及研究投入力度及侧重点的不足等方面原因，目前鲜有关于路基不均匀沉降对有砟轨道影响等方面的相关研究报道.

因此，作者在前期关于路基不均匀沉降引起轨面沉降的试验研究基础上［11］，采用连续弹性点支承梁模型［12－14］的矩阵解法来计算钢轨的沉降变形，模型中为计算路基不均匀沉降对钢轨沉降变形的影响，引入非线性边界的概念来模拟路基的不均匀沉降，并假定道砟不能承受拉应力，得到了路基不均匀沉降引起轨面沉降变形的计算方法.

1 钢轨的弹性点支承梁简化模型

轨道结构由钢轨、轨枕、道床等连接组成，轨道支承在路基上，上部承受列车荷载.轨道结构示意图如图1所示.

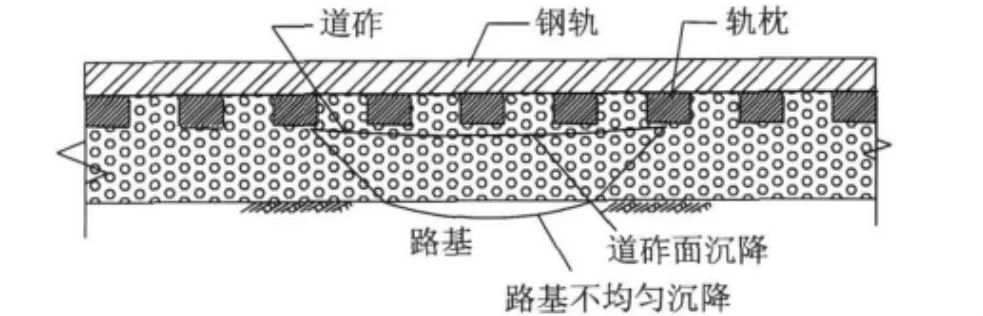
图1 轨道结构示意图Fig.1 Sketch map of track constructure

为计算路基不均匀沉降引起的轨面沉降变形，假定路基为刚体，路基的不均匀沉降在道砟中以一定角度向上传递，引起道砟面产生一定范围的沉降，形成道砟面沉降槽，如图1所示.根据作者前期试验研究结果分析［11］，路基不均匀沉降可采用余弦型函数描述，道砟面沉降槽面积与路基不均匀沉降槽面积存定量关系，因此，路基不均匀沉降引起的轨面沉降问题可简化为求道砟面沉降引起的轨面沉降问题.鉴于此，采用梁理论将道砟简化为支承弹簧，由于钢轨与轨枕的钢性连接及轨枕的离散支承特点，钢轨可简化为受连续弹性点支承的梁，道砟面的沉降可简化为钢轨梁的非线性边界条件，假定钢轨为无限长梁，断面大小均匀，所有节点均按弹性支点来处理，支点刚度不等，支点跨度不等，简化模型图如图2所示.

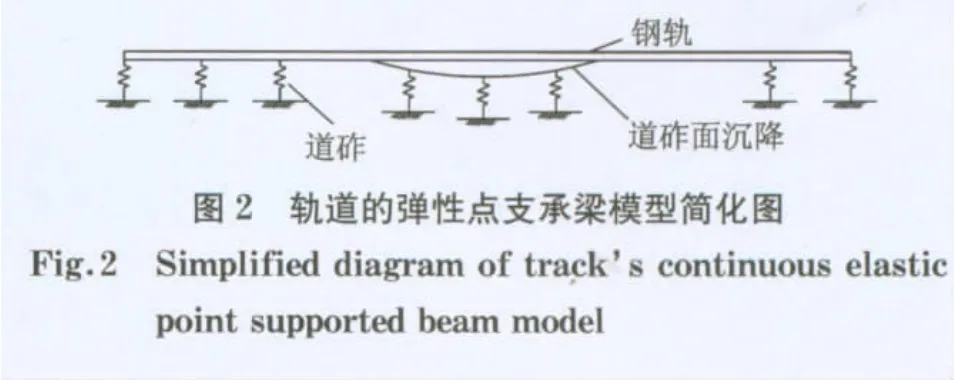
2 路基不均匀沉降引起轨面沉降的计算方法

为得到余弦型路基不均匀沉降大小与钢轨面沉降变形之间的关系，根据文献［11］中模型试验结果，路基不均匀沉降与其所引起道砟面的沉降曲线的形式与面积相等，因此，可将路基沉降与钢轨面沉降之间的关系转化为道砟面沉降与钢轨面沉降之间的关系.

计算模型如图3所示，L为路基沉降的宽度，二支承点间的长度为li（i＝1，2，…，n），假定余弦型道砟面不均匀沉降发生在轨枕i－m与轨枕i＋m之间，余弦型路基不均匀沉降宽度为L′，深度为h′.沿整个轨道纵向每个计算单元节点的路基的沉降为v（xi）（i＝1，2，…，n），取每点的支承刚度为Di（i＝1，2，…，n）.根据弹性支承点不能承受拉力的实际情况，取路基不均匀沉降处的轨枕支点的初始支承刚度为0.外荷载作用于钢轨单元节点上，大小为Pi（i＝1，2，…，n）.计算单元的长度根据轨枕的实际位置和列车荷载的作用位置来确定，通过调整li及Di可实现对应于实际铁路轨道列车荷载作用于钢轨不同位置上的情况.当列车荷载作用于二根轨枕之间时，取荷载作用点的支承刚度为0.

在轨道结构变形稳定的前提下计算路基不均匀沉降引起的钢轨变形时，应扣除钢轨自重应力引起的初始变形，因此在计算模型中（图3），集中荷载P包含了每一段的钢轨的自重及对应点的轨枕自重荷载，荷载P作用引起的路基沉降v（xi）（i＝1，2，…，n）包含了由自重作用引起的变形w0及由路基沉降引起的附加变形.

计算模型根据连续弹性点支承梁计算理论［12－14］，引入非线性边界条件，推导路基不均匀沉降引起钢轨沉降的计算公式.给定的支座变形v0（x）作为该模型的非线性边界条件，v0（x）采用余弦函数表示，假定计算所得钢轨的变形为v（x），则钢轨面所示的外荷载F 可表示如下：

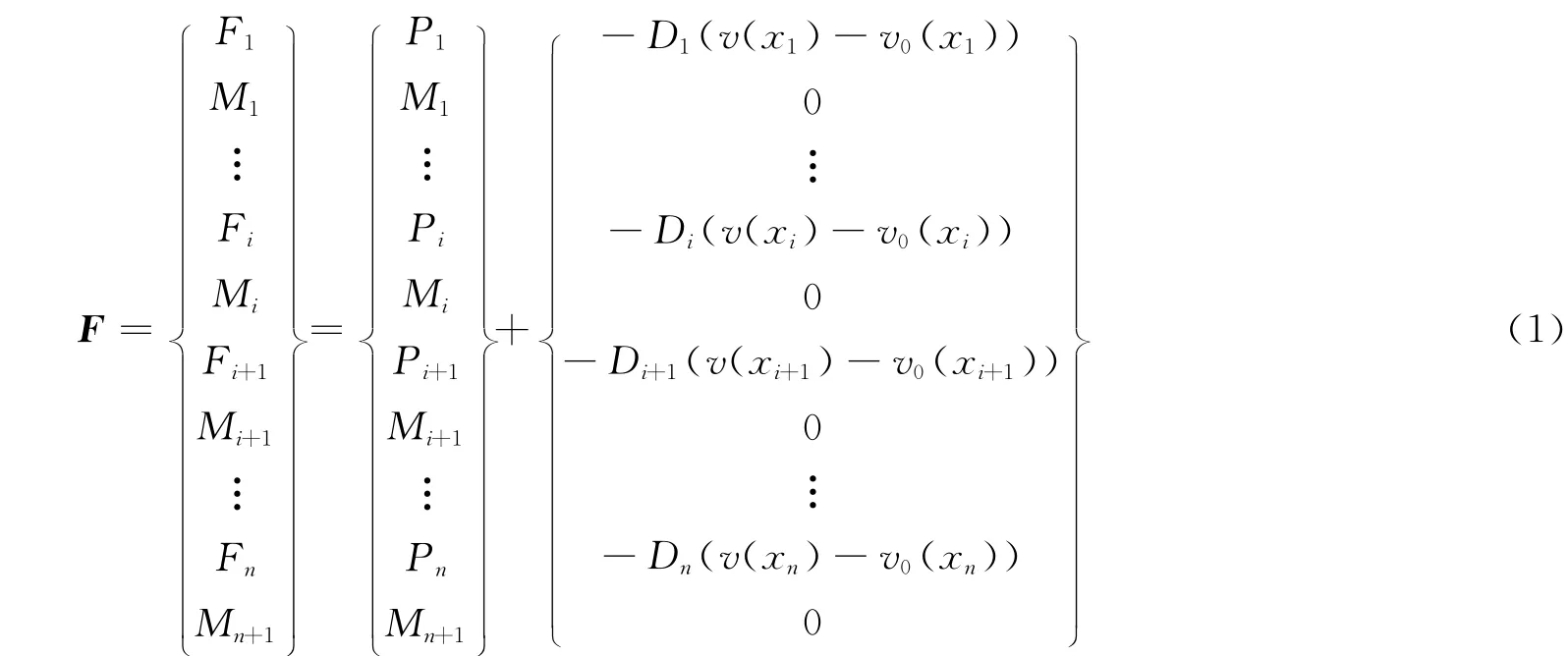
根据连续弹性点支承梁理论，可得力与位移的相互关系，将式（1）中F 列向量中含未知位移v（x）的项移到方程的右边，得

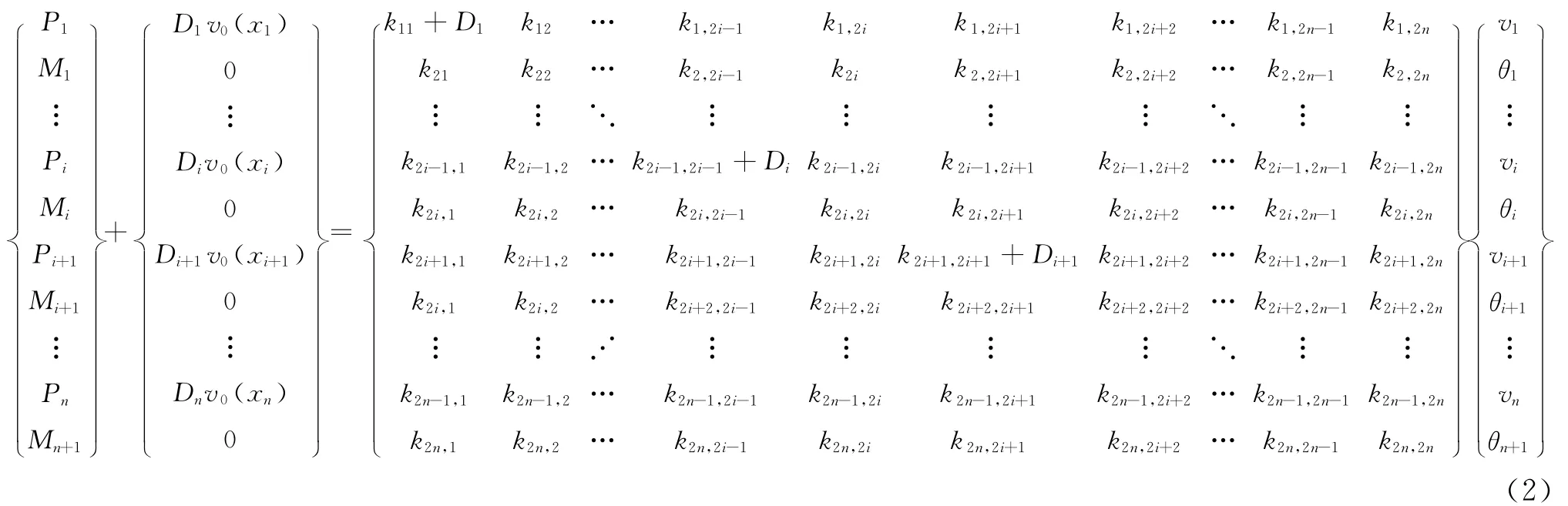
式（1）—（2）中：ki，j为i点产生单位位移，需在j点施加的力的大小；Mi为节点i力偶荷载；vi为节点i位移，θi为节点i转角.

求解式（2）即得路基不均匀沉降引起的钢轨面沉降变形.

考虑钢轨支座不能承受拉应力，引入接触函数（H（vi），i＝1，2，…，n）：

考虑钢轨支座不能承受拉力时，钢轨支承刚度Di可表示为HDi，即当支承受拉时支承反力为0.由于支承刚度的变化，式（2）的求解应采用迭代计算方法.由式（2）计算钢轨挠曲线v（x），判断该区域各支承点v（xi）与v0（xi）的相对大小，若v（xi）＞v0（xi），则接触函数H（vi）＝1，若v（xi）≤v0（xi），则H（vi）＝0.根据支承刚度Di的变化，重新代入式（2）中，计算新的v（x），再重复上述过程计算新的H（vi）的大小，如此迭代计算直到该区域前后二次计算的钢轨的变形差值足够小.

3 工程实例验证分析

3.1 工程概况

上海市轨道交通2号线的西延伸工程位于青浦区、闵行区、长宁区境内.共包含3站3区间，均为地下线路，线路终点与2号线淞虹路站相接.其中诸光路站至虹桥西站区间，全长约1 394.957m，线路平面最小曲线半径650 m，最大曲线半径1 000 m.线路纵断面呈“V”字形，最小坡度2‰，最大坡度23.182‰.隧道覆土厚度最小为8.789 m，最大为17.814m.采用单圆盾构隧道施工方法，盾构隧道外径为6.2m.

该区间隧道在里程SK1＋140处下穿沪昆铁路线，穿越点距离诸光路站始发井约341m，距离旁通道约44.5m，铁路与隧道间的夹角为88°.穿越点的平面示意如图4所示.

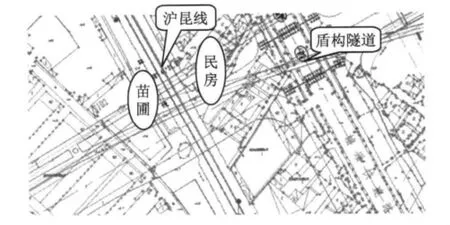
图4 穿越点平面示意图Fig.4 Schematic plan of shield crossing point

盾构施工推进过程中将引起地基土体不均匀沉降，从而使上方铁路线路轨面变形，影响铁路行车安全性；铁路的行车荷载又使盾构管片承受附加动应力的长期作用，增大地基的不均匀沉降，从而影响隧道结构的安全性及耐久性.因此需要采取必要措施对铁路线路基础及地基进行主动加固，以保证施工期及运营期的铁路及盾构隧道结构的安全.

3.2 沪昆铁路路基与轨面沉降测点布置

根据设计要求，结合施工环境和地质情况，本工程的监测主要由盾构隧道洞外监测和周围环境监测两部分组成，在盾构推进前先在地面上布置好变形观测点.在穿越区设置2道横向路基沉降观测断面，铁路两侧道床边缘各设置一个断面；横向观测断面上沉降点位采用钢深层沉降点，在铁路轨枕上设置水杯装置及电子水平尺量测装置.其中铁路上、下行线共设置10个水杯，用于观测轨道结构变形情况；在铁路上行线设置电子水平尺，以对轨面变形情况进行24h监控.布置情况如图5所示.

图5 水准、水杯及电子水平尺测点布置图（单位：m）Fig.5 Station layout of level，cup and electronic levelling rule（unit：m）

3.3 实测结果及分析

下行线盾构于2008年12月24日到达西侧次加固区，开始穿越沪昆铁路.

3.3.1 路基沉降监测数据

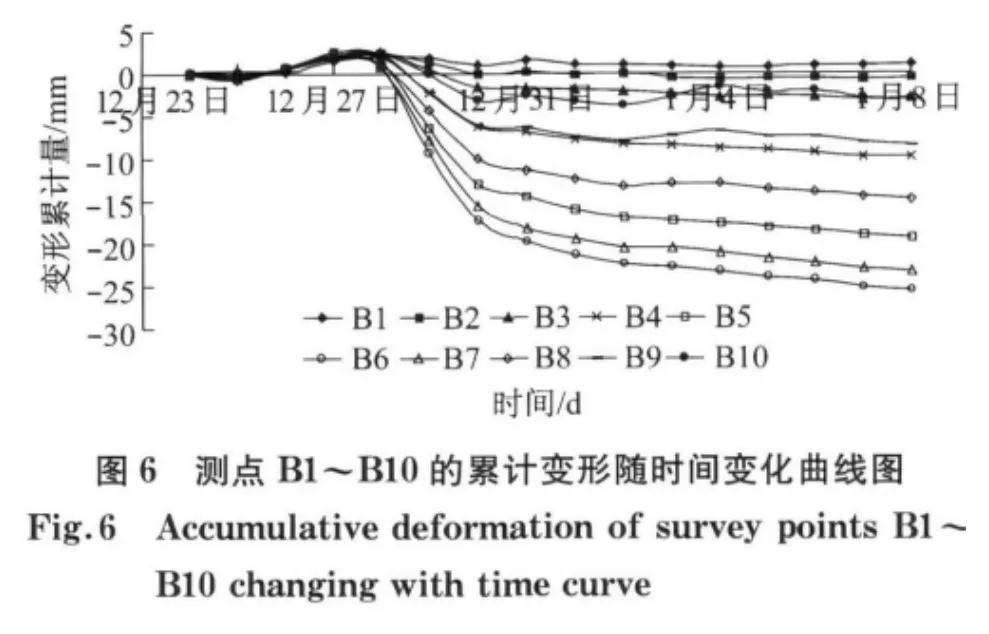
图6为盾构下行线穿越铁路施工期间，垂直于盾构推进方向的B断面路基沉降各监测点累计沉降量随时间变化曲线，其中，正值表示隆起，负值表示沉降，盾构穿越过程中，路基沉降随之增加，并最终趋于稳定.图7为下行盾构推进引起B 断面路基沉降累计变形曲线图，图中可以看出路基沉降槽的宽度约为30m，最大路基沉降为25.45mm.

3.3.2 轨面沉降监测数据

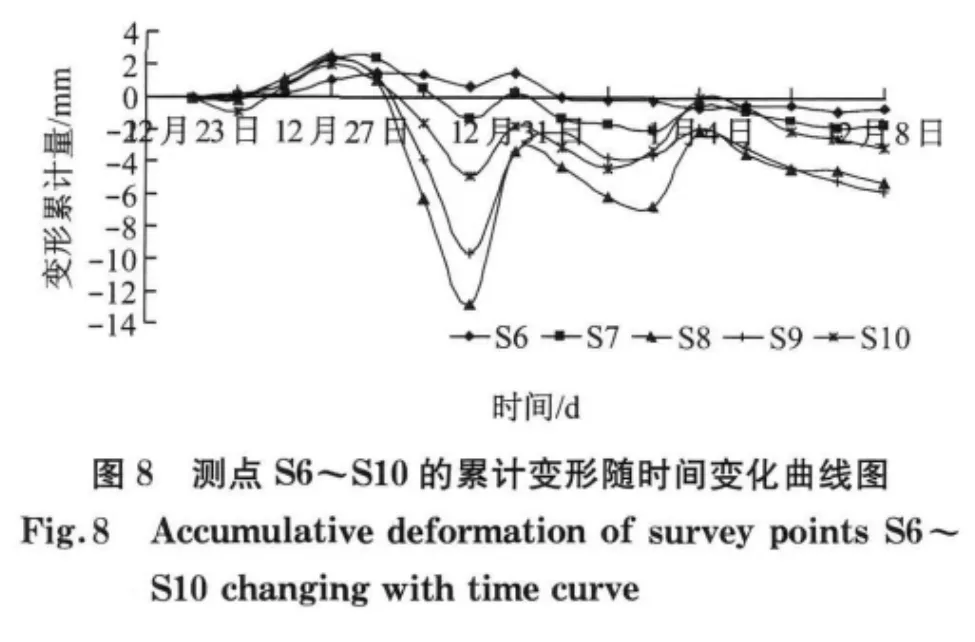
图8为盾构下行线穿越铁路施工期间，垂直于盾构推进方向的轨道沉降各监测点累计沉降量随时间变化曲线，其中，正值表示隆起，负值表示沉降.由于工务部门的整道起道工作，轨道的沉降变形累计量随时间变化规律不明显，轨道沉降变形较小.图9为下行盾构推进引起垂直于盾构推进方向的轨道沉降各监测点每次观测沉降变化量随时间变化曲线，从图中可以看出，在整道起道过程中，轨道结构变形的单次变化量较大，最大起道量为18 mm.图10为下行盾构推进引起测点S6～S10轨道沉降累计变形最终曲线图，由于测点布置宽度有限，从图中不能直接读出沉降槽的宽度，但根据盾构施工引起地面沉降变形的对称性特点，从图中沉降曲线可以看出轨道沉降槽的宽度约为32 m，最大路基沉降为5.95 mm.

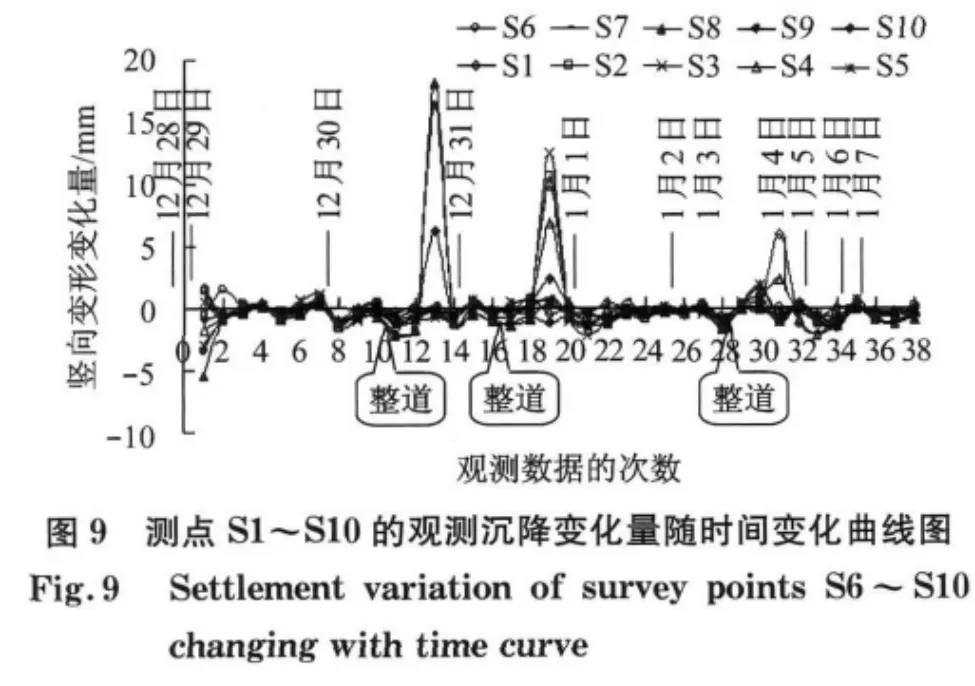
3.3.3 轨道结构监测数据处理分析

为消除整道起道作业对轨道结构面监测数据的影响，对轨道结构面沉降测点的变化量随时间变化曲线（图10）进行处理分析.对三个整道起道工作节点，将起道引起的轨面隆起量归零，同时取起道前一次量测轨面沉降增量作为本次测量记录的轨面沉降增量，最后，将各次轨面沉降增量进行累加，得最终各测点轨面沉降累计变形量，如图11 所示.由于测点布置宽度有限，从图中不能全面反映出沉降槽的宽度，但根据盾构施工引起地面沉降变形的对称性特点，从沉降曲线可以估算出轨道沉降槽的宽度约为32m，最大轨面沉降为25.15mm.

3.4 轨道结构沉降矩阵法计算与实测数据对比分析

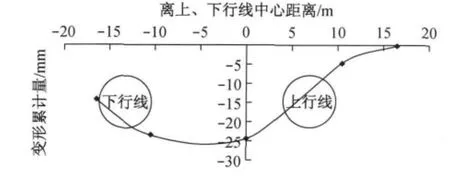
图11 消除起道影响后测点S6～S10沉降累计变形Fig.11 Accumulated settlement of survey points S6～S10after clear the influence of track lifting

将图7下行盾构推进引起B断面路基沉降累计变形曲线设定为初始已知条件，取余弦型路基沉降槽的宽度约为30m，路基沉降幅值为25.45mm，根据盾构法施工经验，该路基沉降不会导致轨枕空吊现象.因此，可采用文献［11］提出的轨枕不空吊情况下，路基不均匀沉降引起轨面沉降变形的计算公式计算轨面沉降，并同时采用本文推导的轨面沉降理论计算公式进行计算.现将采用二种方法计算结果，与实测轨面沉降进行对比分析.

由式（4）：

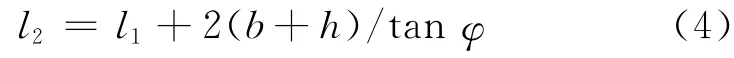
式中：l1为全波余弦型路基不均匀沉降的波长，且l1＝30m；l2为全波余弦型轨面沉降槽的波长；根据模型试验结果，取路基沉降经道砟与钢轨作用后传递到钢轨面的变形扩散角为与竖向成65°，则φ＝25°；b为道砟厚度，b＝0.35m；h为轨枕高，h＝0.28m，则有l2＝32.7m.再由δ2＝δ1l1／l2，其中，δ1为路基沉降波幅，δ1＝25.45mm，l2为全波余弦型轨面沉降槽的波 长，l2＝32.7 m.则 轨 面 沉 降 波 幅δ2＝23.35mm.

采用本文理论计算方法计算时，将图8中路基不均匀沉降曲线沉降槽的宽度取30m，最大轨面沉降25.45mm，代入所编的C＋＋程序即可计算出轨面沉降.

现将两种方法计算所得轨面沉降槽的宽度与幅值与实测结果进行对比，结果如图12所示.

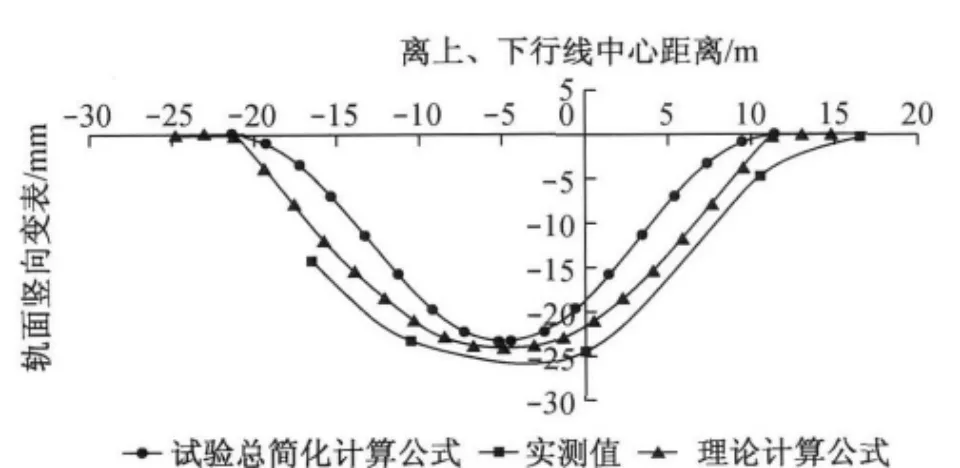
图12 轨面沉降计算结果与实测值对比Fig.12 Comparison of the calculated track settlement and measured value

由图12可知，采用本文理论推导的计算方法的计算结果与实测结果较为接近，钢轨面沉降槽宽度与实测结果基本相同，沉降幅值相差不到1mm（约为轨面沉降值的4%）.计算公式计算所得钢轨面的沉降槽宽度与幅值都比实测值略小，但相差不大，表明理论计算与实际情况较为吻合，证明了理论计算的正确性.

4 结论

（1）考虑轨枕不能受拉的情况，通过引入描述余弦型路基不均匀沉降的非线性边界条件，提出基于连续弹性点支承梁模型的路基不均匀沉降引起轨面沉降的理论计算公式.

（2）对上海市轨道交通2号线西延伸工程盾构法隧道下穿沪昆铁路线工程，路基实测沉降数据及轨道沉降数据进行分析，结果表明路基沉降随盾构下穿施工过程而逐渐增加并最终趋于稳定，轨道沉降由于起道的原因需特殊处理.

（3）将路基不均匀沉降引起的轨面沉降计算方法应用于实际工程中，通过将计算结果与实际工程实测结果的对比分析，证明了将本文所提的路基不均匀沉降引起轨面沉降计算方法的正确性.

［1］ 王午生.铁路线路工程［M］.上海：上海科学技术出版社，2000.WANG Wusheng.Railway line engineering［M］.Shanghai：Shanghai Scientific and Technical Publishers，2000.

［2］ 卢祖文.铁路轨道结构及修理［M］.北京：中国铁道出版社，2002.LU Zuwen.Railway track structure and repair［M］.Beijing：China Railway Publishing House，2002.

［3］ 张群.路基不均匀沉降对双块式无碴轨道的影响研究［D］.成都：西南交通大学道路与铁道工程系，2007.ZHANG Qun.Study of doubleblock ballastless track causing by subgrade differential settlement［D］.Chengdu：Department of Road and Railway Engineering of Southwest Jiaotong University.2007.

［4］ 蔡成标，翟婉明，赵铁军，等.列车通过路桥过渡段时的动力作用研究［J］.交通运输工程学报，2001，1（1）：17.CAI Chengbiao，ZHAI Wanming，Zhao Tiejun，et al.Research on dynamic interaction of train and track on roadbed－bridge transition section［J］.Journal of Traffic and Transportation Engineering，2001，1（1）：17.

［5］ Kerr A D，Moroney B E.Track transition problems and remedies［J］.Bulletin 742—American Railway Engineering Association，1995（742）：267.

［6］ Monley G J，Wu T H.Tensile－reinforcement effects on bridgeapproach settlement［J］.Journal of Geotechnical Engineering.1993，119（4）：749.

［7］ 李献民，王永和，杨果林，等.高速下过渡段路基动响应特性研究［J］.岩土工程学报，2004，26（1）：100.LI Xianmin，WANG Yonghe，YANG Guolin，et al.Study on the dynamic response of transition section roadbed subject to high speed［J］.Chinese Journal of Geotechnical Engineering，2004，26（1）：100.

［8］ 韩义涛，姚力.基础沉降对土路基上板式轨道动力性能影响分析［J］.铁道工程学报，2007，10：28.HAN Yitao，YAO Li.Analysis of the dynamic perfor－mance for slab track settlement on embankment［J］.Journal of Railway Engineering Society，2007，10：28.

［9］ 翟婉明，韩卫军，蔡成标，等.高速铁路板式轨道动力特性研究［J］.铁道学报，1999，21（6）：65.ZHAI Wanming，HAN Weijun，CAI Chengbiao，et al.Dynamic properties of high－speed railway slab tracks［J］.Journal of the China Railway Society，1999，21（6）：65.

［10］ 曾树谷.铁路散粒体道床［M］.北京：中国铁道出版社，1997.ZENG Shugu.Railway granular ballast bed［M］.Beijing：China Railway Publishing House，1997.

［11］ 邹春华，周顺华，王炳龙，等.路基不均匀沉降对有砟轨道沉降变形影响的模型试验研究［J］.同济大学学报：自然科学版，2011，39（6）：862.ZOU Chunhua，ZHOU Shunhua，WANG Binglong，et al.Model test study of influence of differential subgrade settlement on settlement of ballasted Track［J］.Journal of Tongji University：Natural Science，2011，39（6）：862.

［12］ Ghali A.Structural analysis［M］.London：Spon Press，2003.

［13］ 邢书珍.铁路轨道强度计算的新方法［J］.铁道学报，1985，7：66.XING Shuzhen.A new method for calculating railway track strength［J］.Journal of the China Railway Society，1985，7：66.

［14］ 何芳社，钟光路.无拉力Winkler地基上梁的脱离问题［J］.西安建筑科技大学学报：自然科学版，2004，36（1）：48.HE Fangshe，ZHONG Guanglu.Bending of unbonded contact of beams on tensionless winkler foundations［J］.Journal of Xi’an University of Architecture ＆Technology：Natural Science，2004，36（1）：48.