承载力退化体系中各延性系数下的地震力计算

童根树，叶 赟，2，张 磊

（1.浙江大学 土木工程学系，浙江 杭州310058；2.浙江大学 建筑设计研究院，浙江 杭州310027）

节点和构件具有的塑性变形能力反映了结构在地震时经受不可恢复的变形和消耗地震能量的能力，表征这种能力的指标是延性系数.目前国内外文献对如何定义延性系数有不同做法，变形能力和屈服位移的取值存在多种约定.

Park［1］总结对比了4 种定义屈服位移Δy和最大位移Δu的方法，认为混凝土结构的屈服位移Δy的取法应该取原点和曲线段上0.75Pmax点（Pmax为峰值承载力）的连线和直线y＝Pmax的交点，如图1所示，最大位移取Pmax时对应的位移是相对保守的，承载力下降一定数值时对应的位移是更接近于实际的最大位移.Park并没有给出具体的下降值.

Kazemi［2］定义位移延性系数时屈服位移Δy的取法和Park相同，极限位移Δu则取承载力下降到峰值承载力的80%时对应的位移（图1）.Usami等［3］采用了两种延性定义，δm／δy和δ95／δy，屈服位移δy的取法是取曲线直线段的末端，δm为峰值承载力时对应的位移，δ95取承载力下降到峰值承载力的95%时对应的位移，见图2.文献［4］将结构荷载位移曲线采用两折线理想化，第1段取弹性刚度，第2段终点取荷载位移曲线上结构允许达到的最大位移点，两折线的折点的确定则要求两折线下的面积等于曲线下的面积来确定.FEMA356没有规定有效的延性系数如何确定.

等位移准则和等能量准则，都仅与延性系数有关，近二十年的研究［5－6］也表明，延性系数是决定地震力的决定性因素，因此最大位移和屈服位移的取值非常重要.但是人为给定一个方法（例如人为给定下降15%的点作为计算最大位移的点），不仅难有依据，也不易被广泛接受.

本文研究承载力有退化模型的地震力折减系数.考察位移延性系数μ＝Δmax／Δy相同时，不同承载力退化程度（例如变形达到Δmax＝μΔy时承载力退化10%，20%，30%等等）的模型，分析对比其地震力折减系数的差别.通过这种分析，了解不同延性系数定义下对应的地震力的差别，进而得到与退化模型等效的理想弹塑性模型，为地震力计算的合理化提供依据.

1 分析方法

如规范CECS160—2004［7］中，通过对中震弹性地震力折减来获得弹塑性地震力，采用

式中：Fe为弹性地震力，R＝1／C为相应的地震力调整系数，它与μ有关.

给体系输入地震波，进行弹塑性动力时程响应分析，研究其延性开展，与设定的延性能力进行比较，有差别时调整屈服承载力，直至延性开展与设定的延性能力相等，这样确定的屈服承载力就是设计应该采用地震力，与弹性最大基底剪力的比值即为结构影响系数.对结构体系输入大量不同地震波进行分析，对数据进行统计分析，得到各种弹塑性反应谱.

理想弹塑性（elastic－perfectly plstic，EPP）体系在给定延性下的地震力是

式中：R0为理想弹塑性体系的地震力调整系数；Vy为地震承载力的峰值.记K为初始弹性刚度，K′为后期刚度，α为后期刚度系数（可为负），则有

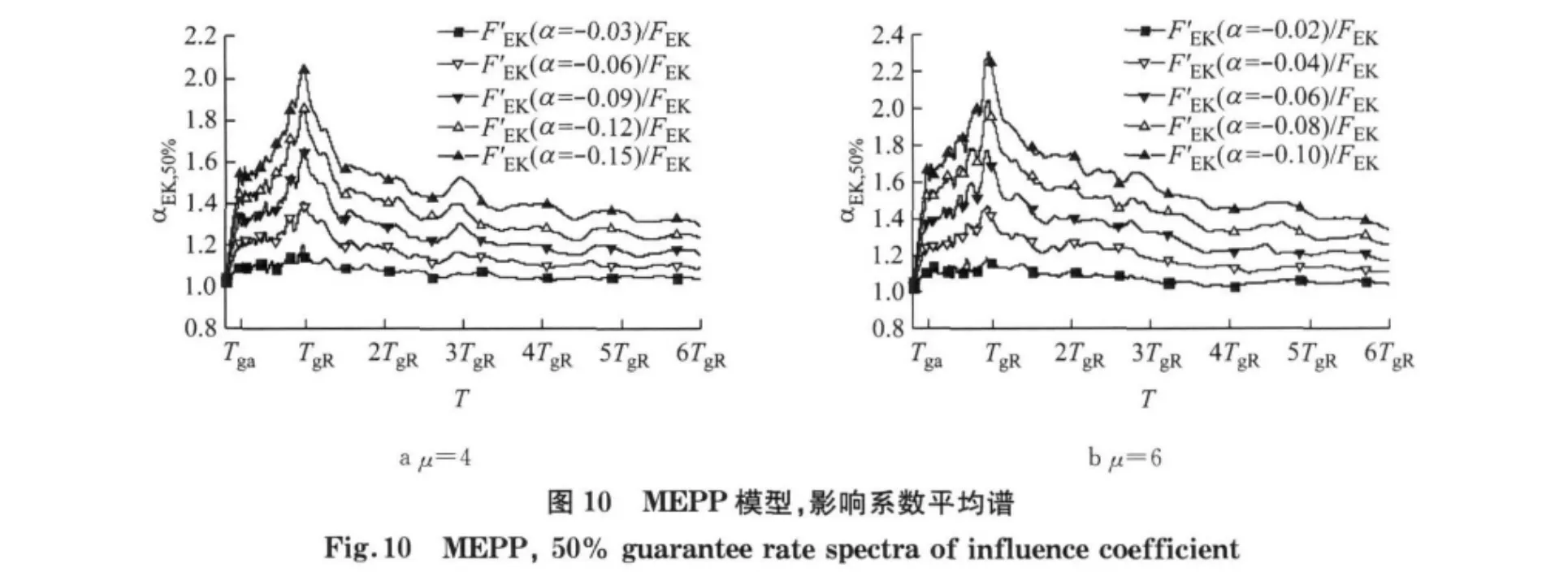
ΔVy是变形达到最大值时地震承载力的退化量：

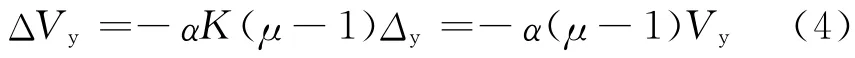
式（5）—（6）中：F′EK为有退化模型的地震力；ΔFEK为有退化模型的地震力相对于EPP 模型的地震力的变化；R′为有退化体系的地震力调整系数.

可得承载力退化值和后期刚度系数关系，见表1.

表1 承载力退化值和后期刚度系数α 关系Tab.1 Relationship of strength degrading and poststiffness factors

从美国Berkeley大学地震工程研究中心网站上下载地震加速度纪录共370条，各地震记录的加速度反应峰值对应的周期是Tga，地震力调整系数Rμ谱峰值点对应的周期是TgR［8－9］.四类场 地统计平均意义上的Tga分别为：0.307，0.364，0.404，0.494s；TgR分别为：2.244，2.096，2.347，3.166s.在统计平均的意义上，TgR是Tga的5.5～6.7倍.反应谱曲线上将周期分为0～Tga，Tga～TgR和TgR～6TgR三段：在0～Tga段，用Tga对周期量纲一化；在TgR～6TgR段，周期用TgR量纲一化；在Tga～TgR段，将区间分成100段，获得99个内插值点，对所有地震波下的99个点的谱值直接相加并进行统计分析.

图3是真实地震波下人字撑框架和人字撑架抗侧力与层侧移角的关系，层侧移角定义为层间位移与层高的比值，见文献［10］第十章.据此抽象出承载力退化条件下的EPP滞回曲线模型如图4所示，称为 修 正 理 想 弹 塑 性（modified elastic－perfectly plastic，MEPP）模型.图中，V′y为考虑不同参数组合下的地震承载力的峰值.

图3 支撑架的滞回曲线Fig.3 Hysteretic response of braced frames

图4所示，当位移越过屈服位移Δy（1点），结构进入屈服后阶段，承载力退化至2点；此后以初始刚度卸载，由于V′y＝Vy，到3点后，承载力不退化；继续到达原始屈服压位移，即4点；如继续卸载，承载力退化至5；此时结构有最大输入加速度，速度反向，以初始刚度加载，到达Vy（6点）后，承载力不退化，至7点（上一步最大位移，2点），如此结构做反复振动.

图4 MEPP模型示意图Fig.4 Schematic diagram of MEPP models

利用MEPP及剪切滑移（SSP）、双线性（BIL）模型，通过自编C＋＋程序得到了考虑不同自振周期、延性、承载力退化系数等参数组合下的双周期标准化的地震力调整系数Rμ.其中SSP模型是剪切滑移模型（shear－slip model），具有一次性耗能能力（oneoff），描述中心支撑长细比很大的框架的恢复力特征；BIL 模型是无耗能能力的二段式弹性模型（bilinear－model），可描述橡胶支座.

定义θ为P－Δ二阶效应系数［8－10］.MEPP模型和EPP模型受到P－Δ效应的最大区别在于，图4a中的V′y＝Vy，且y＜Δy时，K′＝K，文献［9］中V′y＝（1－θ）KΔy＜Vy，且y＜Δy时刚度是（1－θ）K＜K，故刚度退化系数与二阶效应系数相等时，二阶效应对模型的影响更大.

单条地震力分步计算中，在α＝－0.1，θ＝0.05，μ＝6，T＝TgR的条件下输入A 类1060－N－AT2＿01地震波.在地震波加速度输入过程中，输出位移Δ和恢复力F的关系，最后得出的修正EPP模型滞回曲线模型.由图5可见，程序是准确的.

2 修正EPP模型

2.1 地震力调整系数Rμ 谱

图5 MEPP模型示意图Fig.5 Output diagram of MEPP model

μ＝2，θ＝0，阻尼比ξ＝0.05时，四类场地刚度退化系数α分别为0、－0.1、－0.2、－0.3、－0.4、－0.5时的地震力调整系数Rμ谱如图6所示.图中，Rμ，50%为地震力调整系数的平均谱.考虑承载力退化系数后：

（1）承载力退化模型的地震力调整系数较α＝0均下降.承载力退化会导致由来回振动转变到单向偏移的现象，导致更大的侧向位移.位移增大，意味着在相同调整系数情况下，延性需求增大，进而削弱了结”构的防倒塌能力.为了获得与不考虑承载力退化系数时相同的延性需求，必须减小调整系数，以减小位移.

（2）对于相同位移延性系数，特定的自振周期T，地震力调整系数Rμ随承载力退化绝对值的增大而减小，在0＜T＜Tga段基本相同，在Tga＜T＜6TgR变化幅度相对较大，T＝Tga和T＝TgR时存在峰值.

（3）长周期下，随周期延长，整体变化趋于接近.

（4）四类场地的标准化Rμ谱非常接近，场地类别依然是影响Rμ的主要因素之一，其影响隐含在横轴周期中.总体而言，D 类场地下的地震力调整系数最大.

A～D 四类场地Rμ的变异系数Cov谱如图7所示，各类场地Cov均在0.2左右波动.不同承载力退化下的谱也非常接近.

2.2 基底剪力的承载力退化影响系数αEK

为了反映承载力退化对地震基底剪力的影响，引入参数αEK＝F′EK／FEK＝Rμ，0／Rμ，α（Rμ，0指α＝0时的Rμ，Rμ，α指不同α值但不为0 时的Rμ），如α＝－0.5，μ＝2时，A 类场地下，共106条地震波，每条地震波200个数据点，总共21 200 个F′EK／FEK数据，其平均谱即为

图8为μ＝2时MEPP模型的影响系数平均谱.图8表明：T接近于0时，αEK都趋近于1；T＜Tga时，αEK受周期变化的影响显著，基本随线性增加；Tga＜T＜TgR时，除去两个周期处的峰值及其邻近区域，中间段存在一个水平波动段.TgR＜T＜2TgR时，αEK逐渐下降；T＞2TgR时，αEK相对稳定，α＝－0.5趋近于1.3，这个差别在抗震设计中是不容忽视的.

由图8知，D 类场地影响系数谱αEK在相同承载力退化值时最大.为得到承载力退化值相同但延性不同对MEPP 模型影响系数谱αEK的影响，图9 给出了D类场地，θ＝0，ξ＝0.05，μ＝4，6时MEPP模型Rμ谱，曲线形状与μ＝2时类似，谱值不同.

影响系数αEK谱见图10.μ＝4和μ＝6时刚度退化取值和μ＝2时不同，但承载力下降的幅度和μ＝2时相同或者接近，αEK的曲线形状粗略地相似.μ＝4，6时，αEK在T＝Tga处的波峰几乎消失，然后增加，直到TgR处达到最大值，然后以较慢的速率下降，μ越大，下降越慢.对比图10和图8可知，承载力退化的幅度是比退化刚度更为重要的参数，地震力延性系数谱直接与承载力的下降幅度成正比.

2.3 基底剪力的影响系数拟合谱

从前面分析得到：不同承载力退化值及不同延性系数时的影响系数是不一样的，两者都对影响系数产生显著影响，拟合如下：

其中：

D 类场地，θ＝0，ξ＝0.05，μ＝2，4，6 时部分拟合结果对比如图11所示.图中，以实心图例表示的代表计算值，以空心图例表示的曲线为拟合曲线.

图11 MEPP模型，影响系数拟合谱Fig.11 MEPP，50%guarantee rate spectra of the influence fitting coefficients

2.4 与退化模型等效的理想弹塑性模型

αEK的物理意义是：退化体系与理想EPP体系的延性系数相同、初始刚度相同的结构，承载力需求的比值.如图12所示，Δmax和Δy分别为理想弹塑性体系最大位移和屈服位移；Δ′max和Δ′y为有退化模型最大位移和屈服位移；两者初始刚度相同，延性系数相同，则：

因此等效模型的屈服位移和最大位移分别为

式（15）—（16）写成

即：如果结构承载力有退化，那么为了得到与理想弹塑性模型的延性等效（即具有相同的抗震性能），则对有退化的结构的承载力的要求是理想弹塑性结构的αEK倍，对变形能力（绝对值）的需求也是相同延性系数的理想弹塑性模型的αEK倍.

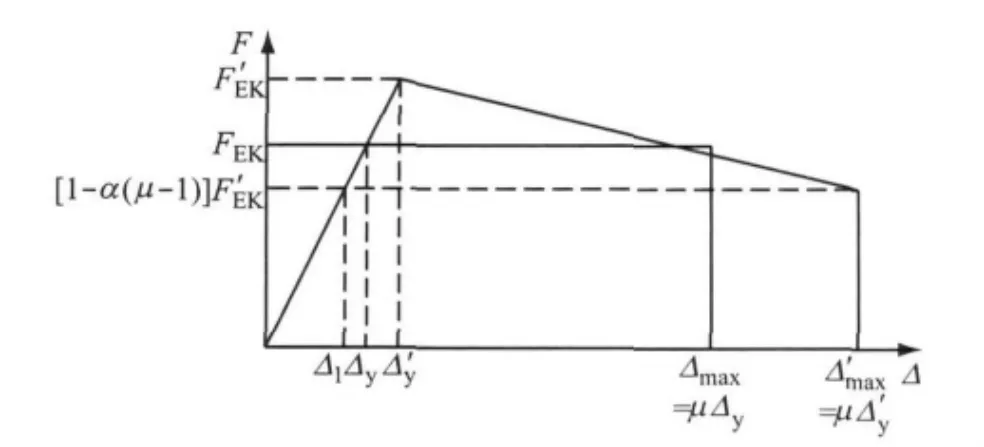
图12 MEPP模型与EPP模型等效Fig.12 MEPP model with its equivalent EPP model

3 SSP模型

如图13所示，θ＝0，ξ＝0.05，μ＝2，4，6时B 类场地不同承载力退化系数时SSP 模型的Rμ谱与MEPP模型相比，Rμ谱稍有降低，不同承载力退化曲线更加趋近.与无退化的SSP模型的比值如图14所示.影响系数谱与MEPP 模型相比最大不同在于其峰值只有一个，在T＝Tga处，其值约为1.25.T接近于0时αEK趋近于1；T＜Tga时，αEK基本随T线性增加；Tga＜T＜6TgR时，αEK虽有波动，但总体下降，慢慢趋于平缓.承载力退化对其曲线影响较MEPP模型小.

4 BIL模型

图15 BIL 模型，平均谱Fig.15 BIL model，50%guarantee rate spectra

θ＝0，ξ＝0.05，μ＝6，退化系数α分别为0、－0.02、－0.04、－0.06、－0.08、－0.10时，对BIL模型在D 类场地下的地震力调整系数R′μ进行了分析，如图15所示.各场地标准化的R′μ谱形状相似，谱值稍有差别.其在Tga＜T＜TgR时的R′μ谱基本没有变化；在TgR＜T＜2TgR时，承载力退化系数α绝对值越大，减小得稍多，当α＝－0.1时减小13%左右，远小于修正EPP（MEPP）模型和SSP模型，可见承载力退化对BIL模型的影响很小.

5 结 论

本文考虑了延性和承载力退化影响，对三种有退化MEPP，SSP，BIL 模型相关的地震力调整系数谱进行研究，谱曲线以周期Tga和TgR进行双周期标准化，保留了R谱在Tga和TgR处的峰值特征.结论如下：

（1）MEPP模型的承载力退化值对地震力调整系数影响很大，SSP模型次之.BIL 模型有很强的恢复到原点的能力，承载力的后期退化对其调整系数谱几乎没有影响.

（2）实践中取承载力退化多少来定义延性系数，根据本文的研究发现对SSP，BIL 模型可以适当放宽要求.对退化的MEPP模型，得到了与承载力退化模型等效的理想弹塑性模型.即有退化的结构的承载力的要求是理想弹塑性模型的αEK倍，同时对变形能力的需求也是理想弹塑性模型的αEK倍.

［1］ Park R.Ductility evaluation from laboratory and analytical testing［C］／／Proceedings of Ninth World Conference on Earthquake Engineering.Tokyo－Kyoto：IAEE，1988：605－616.

［2］ Kazemi M T.Seismic shear strengthening of R／C columns with ferrocement jacket［J］.Cement and Concrete Composites，2005，27：834.

［3］ Usami T，Ge H B.Cyclic behavior of thin－walled steel structures—numerical analysis［J］.Thin－Walled Structures，1998，32：41.

［4］ FEMA356.Prestandard and commentary for the seismic rehabilitation of buildings［S］.Washington D C：Federal Emergency Management Agency，2000.

［5］ Vidic T，Fajfar P，Fischinger M.Consistent inelastic design spectra：strength and displacement ［J］. Earthquake Engineering and Structural Dynamics.1994，23：507.

［6］ Mahin S A，Bertero V V.Problems in Establishing and predicting ductility in structural design［C］／／Proceedings of the International Symposium on Earthquake Structural Engineering.Missouri：［s.n.］，1976：613－628.

［7］ 中国工程建设标准化协会.CECS160—2004 建筑工程抗震性态设计通则（试用）［S］.北京：中国计划出版社，2004.China Engineering Construction Standardization Society.CECS160—2004 General rules for performance－based seismic design of buildings［S］.Beijing：China Planning Press，2004.

［8］ Zhao Y F，Tong G S.An investigation of characteristic periods of seismic ground motion ［J］.Journal of Earthquake Engineering，2009，13：540.

［9］ 蔡志恒，双周期标准化的弹塑性反应谱研究［D］.杭州：浙江大学土木工程学系，2011.CAI Zhiheng.Inelastic spectra normalized by two characteristic periods［D］.Hangzhou：College of Civil Engineering and Architecture of Zhejiang University，2011.

［10］ 罗桂发，钢支撑和框架的弹塑性抗侧性能及其协同工作［D］.杭州：浙江大学土木工程学院，2012.LUO Guifa.Elastic－plastic resistances of steel brace，momentresisting frame and their cooperation in dual system［D］.Hangzhou：College of Civil Engineering and Architecture of Zhejiang University，2012.