不等式证明的高等数学方法研究

吴凤珍

(郑州职业技术学院 数学教研室，河南 郑州 450121)

不等式证明的高等数学方法研究

吴凤珍

(郑州职业技术学院 数学教研室，河南 郑州 450121)

不等式是研究数学问题的工具，证明不等式对培养学生的创新思维能力有着极其重要的作用，但是不等式证明的高等数学方法的研究一直缺乏系统的理论层面的提升.分析并总结了高等数学中证明不等式的几种主要方法及其适用条件.

不等式;证明;高等数学;方法

0 引言

不等式是研究数学问题的重要工具，它渗透在数学的各个部分，在高等数学中也有极其重要的作用.证明不等式是高等数学中的常见题型，也是难度较大的题型之一，在专升本和考研试卷中也经常出现.不等式证明的基本方法很多，但是有关不等式证明的高等数学方法的研究一直缺乏系统的理论层面的提升. 本文对不等式证明的高等数学方法进行了比较系统的研究，并对每种方法的适用情形进行了探讨，以期能拓宽学生的解题思路，培养他们的创新精神及创新思维能力.

1 微分学方法

1.1利用函数的单调性

如果证明不等式f(x)gt;g(x)，一般优先考虑此方法，其通常步骤为：

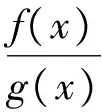
(2)求出F(x)，由F′(x)的符号判断F(x)在相应区间上的单调性.

例1 求证：当xgt;0时，有

利用函数的单调性证明不等式的关键是构造辅助函数，构造的方法有两种：作差或作商.一般先作差，若作差不能成立时，再用作商的方法.在判断辅助函数F(x)的单调性时,有时需借助于F″(x)或更高阶导数的符号来得到F′(x)的符号.

1.2利用函数的最值(或极值)

这种方法的适用情形与上述方法类似,只是当构造的辅助函数在给定区间上不单调或是遇到f(x)≥a或f(x)≤b(a，b为常数)类型的不等式时，可采用最值方法.这种方法的基本步骤是:

(1)构造辅助函数,当不等式两边均含有未知数时,可利用不等式两边之差构造辅助函数，当不等式形如f(x)≥a或f(x)≤b时,可设f(x)为辅助函数;

(2)求出辅助函数在区间上的极值或最值.

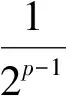
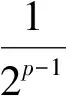
1.3利用函数的凹凸性

当证明的不等式的两边或一边是同一函数在不同点处的函数值的叠加时，一般需要通过将不等式适当变形构造辅助函数, 利用函数的凹凸性证明之.[1]

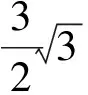
分析：不等式左边为sinx的函数的和，考虑构造凹函数f(x)=-sinx.

证明:令f(x)=-sinx,0lt;xlt;π，则f″(x)=sinxgt;0 .则f(x)是(0,π)上的凹函数,由函数的凹凸性容易证得

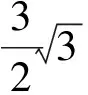
1.4利用微分中值定理

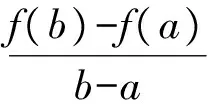
f(b)-f(a)=f′(ξ)(b-a)其中ξ∈[a,b],再根据ξ的取值范围对f′(ξ)进行估计,进而得出不等式关系.

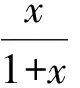
证明：构造函数f(t)=lnt，因f(t)在[1,1+x](xgt;0)上满足拉格朗日中值定理的条件，容易证得

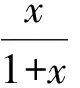
1.5利用拉格朗日乘数法

对于一元不等式,利用函数的极值来证明不等式是一种非常重要的方法,借助拉格朗日乘数法求多元函数的极值就可得到多元不等式的拉格朗日乘数法.当所证不等式中含有二个以上变量时,就可考虑这种方法.用拉格朗日乘数法的关键是选择目标函数和约束条件.如果没有明确告诉约束条件，通常把不等式的“一端”作为目标函数，而将“另一端=常数a”作为约束条件.

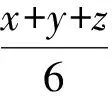
证明:考察函数f(x,y,z)=xy2z3在x+y+z=6a约束条件下的最大值问题，其中a为正常数.构造拉格朗日函数

F(x,y,z,λ)=xy2z3+λ(x+y+z-6a).

它唯一的驻点为(a,2a,3a),此驻点为函数f(x,y,z)=xy2z3的最大值点,

故f(x,y,z)=xy2z3≤f(a,2a,3a).

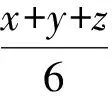
2 积分学方法

2.1利用定积分的定义

当证明的不等式是与自然数n有关的和式时,可考虑利用定积分的定义来证明.这种方法的关键是根据和式的特点构造被积函数和积分区间.

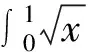
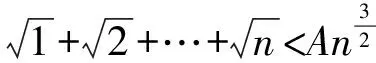
2.2利用积分中值定理

定积分中值定理是在处理含有定积分的不等式中经常用到的理论,其思路是通过中值定理,消去不等式中的积分号,从而与其他项作大小的比较,得出结论.

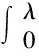
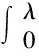
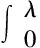
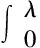
=λ(1-λ)[f(ξ1)-f(ξ2)]≥0,

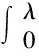
2.3利用积分上限函数

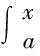
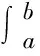
证明：设辅助函数

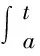
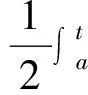
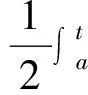
从而F(t)单调递增，所以F(b)≥F(a)=0.

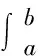
2.4利用重积分

若不等式中含有两个定积分之积,可考虑将其化为重积分,将定积分不等式的证明化为重积分不等式来证明.

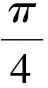
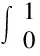
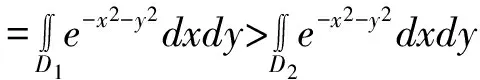
D1:0≤x≤1,0≤y≤1,

D2:x2+y2≤1,x≥0,y≥0,

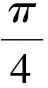
2.5利用柯西—施瓦茨不等式

当不等式中含有带平方项的积分时,往往可通过柯西—施瓦茨不等式来证明.

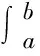
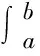
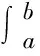
=[g(b)-g(a)]2,

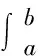
3 其他方法

3.1利用泰勒公式

这种方法适合于题设中含有函数的一阶、二阶及二阶以上的导数且最高阶导数的大小或上、下界可知的命题.运用这种方法时,首先写出比最高阶导数低一阶的函数的泰勒公式,然后根据题设对展开式的余项进行适当的放缩,导出所证不等式.

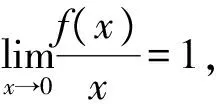
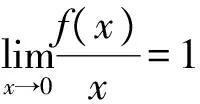
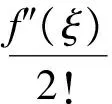
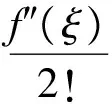
因为f″(ξ)≥0，故f(x)≥x.

3.2利用函数的幂级数展开式

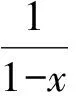
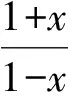
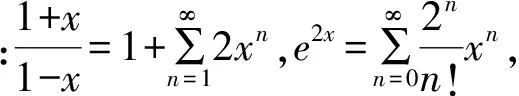
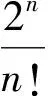
3.3利用二次型的正定性

当遇到有关n元二次齐次式的不等式,我们可考虑用实二次型的半正定或矩阵的半正定性给予证明.

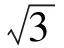
证明：原不等式可化为

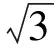
它是一个关于a，b的二元齐次式,令

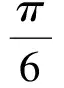
其矩阵为

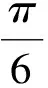
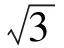
3.4利用概率论

当不等式中出现的数的范围均在0与1之间时,便可利用概率论来证明不等式.利用概率论证明,其基本的思路是将不等式中的数转化为若干个相互独立事件的概率,从而将实数之间的运算转化为概率的运算,利用概率的有关计算公式及性质,便可证得结论.

例14 若0lt;alt;1,0lt;blt;1,证明:

0≤a+b-ab≤1.

证明:令A、B是两个相互独立的事件,且使P(A)=a,P(B)=b,容易证得:

0≤a+b-ab≤1.

3.5利用向量有关知识

构造与问题等价的向量模型,应用向量的有关知识,有时可得到新颖别致的证明.

例15 已知a,b,c,d∈R,证明:

(ac+bd)2≤(a2+b2)(c2+d2).

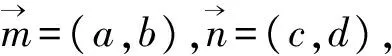
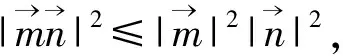
故(ac+bd)2≤(a2+b2)(c2+d2).

4 结论

以上从微分学、积分学、线性代数、概率论等角度将高等数学常用的证明不等式的方法作了研究总结，共三大类15种，但我们遇到具体问题还应该具体分析，有的不等式的证明用到不止一种方法，证明方法的选择也是一种技巧.[6]要想熟练掌握其中的技巧，我们要多思考，多总结．只有灵活运用高等数学的基本理论和方法，才能把握问题的本质，知道怎样人手，思维清晰、简便快捷地解决有关不等式的证明问题.

[1] 吉米多维奇.数学分析习题集题解·二[M].济南：山东科学技术出版社,2003：296-300.

[2] 仓义玲,衡美芹.用多元函数最优化的方法明不等式[J].西昌学院学报,2009(4):33-34.

[3] 徐利治,王兴华.数学分析的方法及例题选讲[M].北京:高等教育出版社,1983：110-112.

[4] 同济大学应用数学系.高等数学·上册[M].北京:高等教育出版社,2002：156-158.

[5] 邓 勇.例谈不等式证明的高等数学方法[J].和田师范专科学校学报,2006(5):189-190.

[6] 张明会，高婷婷.一个数值积分公式的推广[J].四川文理学院学报，2011(2)：17-19.

[责任编辑邓杰]

StudyontheHigherMathematicsMethodoftheInequalityProof

WU Feng-zhen

(Teaching and Research Section of Zhengzhou Vocational and Technical College, Zhengzhou Henan 450121, China)

Inequality is an important tool for studying on higher mathematical problem. Proving inequality is also extremely important in cultivating students′ creative thinking. However, inequality in advanced mathematics to prove the method of the theory has been the lack of system level upgrade. This article studies and summarizes several major approaches to the proof of inequality in higher mathematics and their applicable conditions.

inequality; proof; higher mathematics; method

2012-10-18

吴凤珍(1969—)，女，河南巩义人.副教授，硕士，主要从事高等数学教学研究.

O13

A

1674-5248(2013)02-0010-04