奇阶可裂亚循环p群的各阶子群个数

蔡东平

(陕西国际商贸学院 信息工程学院，陕西 西安 712046)

奇阶可裂亚循环p群的各阶子群个数

蔡东平

(陕西国际商贸学院 信息工程学院，陕西 西安 712046)

p群计数问题是有限p群研究的重要内容之一.关于有限p群的各种类型子群、元素或子集的个数是p群计数问题的重要方面.利用亚循环P群的结构性质计算出了奇阶可裂亚循环p群的各阶子群的个数.

亚循环p群；可裂；P.Hall计数原则

0 引言

p群计数问题是有限p群研究的重要内容之一.关于有限p群的各种类型子群、元素或子集的个数是p群计数问题的重要方面.亚循环p群是一类重要的有限p群.因此，研究亚循环p群的各阶子群个数有重要的意义.

著名数学家徐明曜在文[1]中得到了如下结果：

论断1：有限非交换亚循环p群(p≠2)只有下述两种互不同构的类型：

(Ⅰ)lt;a,b|apn=1,bpm=1,ab=a1+psgt;,n,m,s为正整数，且slt;n,m+s≥n.

(Ⅱ)lt;a,b|apn=1,bpm=apt，ab=a1+psgt;,n,m,s,t为正整数，且s+t≥n,slt;tlt;min(n,m).

下文中为了方便，我们用M(n,m,s)来记可裂的亚循环p群.

其中，当s=0时，M(n,m,0)=lt;a,b|apn=1,bpm=1,[a,b]=1gt;；

当s≠0时，M(n,m,s)=lt;a,b|apn=1,bpm=1,ab=a1+psgt;.即上述定理中的(Ⅰ)型群.

1 主要引理

引理1 若G≌M(n,m,s)，则

由于奇阶亚循环p群是正则的，于是，

下面计算Ωk(G).

当1≤klt;min(n,m) 且lt;apn-kgt;≤G,lt;bpkgt;≤G，lt;apn-kgt;∩lt;bpkgt;=1时，

由lt;apn-kgt;charlt;agt;◁G知lt;apn-kgt;◁G，比较阶可知Ωk(G)=lt;apn-kgt;lt;bpm-kgt;.

当min(n,m)≤klt;max(n,m)时，若nlt;m，lt;agt;≤Ωk(G),lt;bpm-kgt;≤Ωk(G) .又lt;agt;∩lt;bpm-kgt;=1，lt;agt;◁G.比较阶可知Ωk(G)=lt;agt;lt;bpm-kgt; .

同样地，若ngt;m,Ωk(G)=lt;apm-kgt;lt;bgt;.

当k=max(n，m),由exp(G)=pmax(n,m)可知Ωk(G)=G.

引理2 若G≌M(n,m,s)，则

证明:由G正则可知Λk(G)=Ωk(G)，[2]并且由引理1可计算|Ωk(G)|，于是：

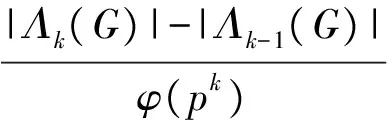
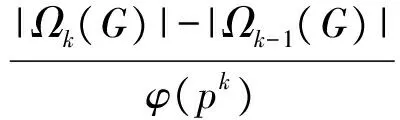
当1≤k≤min(n,m)时，

=pk-1(p+1) ；

当min(n,m)lt;k≤max(n,m)时，

=pmin(n,m).

引理3 奇阶可裂亚循环p群的子群还是可裂的.

证明:若G是交换的可裂亚循环p群，结论显然成了.

若G是非交换的可裂亚循环p群，由论断1可设G=lt;a,b|apn=1,bpm=1,ab=a1+psgt;，n,m,s正整数，且slt;n,m+s≥n.由于d(G)=2,φ(G)=lt;ap,bpgt;，故G的1+p个极大子群分别为：

M1=lt;b,φ(G)gt;=lt;b,ap,bpgt;=lt;b,apgt; ，

Mk=lt;abi,φ(G)gt;=lt;abi,ap,bpgt;

=lt;abi,apgt;,0≤i≤p-1,2≤k≤p+1.

容易看出M1可裂，下面来证Mk是可裂的.

2 主要结论及证明

定理1 若G≌M(n,m,s)，则

sk(G)=

证明:由引理3可知G的所有子群都是可裂的.于是可用归纳法来证明.假设对G的所有真子群都满足结论，现在来证明对G也满足.

(1)当1≤klt;min(n,m)时，由引理1可知Ωk(G)≌M(k,k,s′).于是由归纳假设可得：

sk(G)=sk(Ωk(G))≌sk(M(k,k,s′))=1+p+…+pk.

(2)当min(n,m)≤klt;max(n,m)时，由引理1可知Ωk(G)≌M(min(n,m),k,s′)lt;G.于是由归纳假设可得：

sk(G)=sk(Ωk(G))≌sk(M(min(n,m),k,s′))

=1+p+…+pmin(n,m).

(3)当k=max(n,m)时，由引理2可知ck(G)=pmin(n,m).于是由归纳假设可得：

sk(G)=ck(G)+sk(Ωk-1(G))≌ck(G)+sk(M(max(n,m)-1,min(n-m),s′))

=pmin(n,m)+(1+p+…+pmax(n,m)+min(n,m)-1-k)

=pmin(n,m)+(1+p+…+pmax(n,m)+min(n,m)-1-max(n-m))

=pmin(n,m)+(1+p+…+pmin(n,m)-1)

=1+p+…+pmin(n,m).

(4)当max(n,m)lt;k≤m+n时，由于G不存在pk阶循环子群，并注意到G是亚循环群，从而，G的所有pk阶子群都二元生成.于是，由P.Hall计数原则得：[3]

当k=n+m-1时，

sk(G)=1+p；

当k=n+m-2时，

=(1+p)(1+p)-p

=1+p+p2；

当k=n+m-3时，

=(1+p)(1+p+p2)-p(1+p)

=1+p+p2+p3；

…

当k=n+m-(k′-2)时，

sk(G)=1+p+p2+…+pk′-2；

当k=n+m-(k′-1) 时，

sk(G)=1+p+p2+…+pk′-1；

当k=n+m-k′时，

=(1+p)(1+p+…+pk′-1)-p(1+p+…+pk′-2)

=1+p+…+pk′=1+p+…+pm+n-k.

综上(1)(2)(3)(4)，命题得证.

[1] 徐明曜.奇阶可裂亚循环p群的完全分类[J].数学进展，1983(1):72-73.

[2] 徐明曜，曲海鹏.有限p群[M].北京：北京大学出版社，2010：214.

[3] 徐明曜.有限群导引·上册[M].北京：科学出版社，1999:138.

[责任编辑邓杰]

TheNumberofSubgroupsofSplitMetacyclicGroupsofPrime-powerOrder

CAI Dong-ping

(Shaanxi institute of international trade and commerce ，Xi′an Shaanxi 712046 ，China)

Counting problem is one of the important research contents in finite group of prime-power order.Counting various types of subgroups,element oand the subset is the significant aspect of the problem.This paper gets the number of subgroups of split metacyclic groups of prime-power order.

metacyclic groups of prime-power order；split; P.Hall counting principle

2012-12-07

蔡东平(1984—)，男，河南陕县人.助教，硕士，主要从事有限群研究.

O152.2

A

1674-5248(2013)02-0028-03