Semantic image annotation based on GMM and random walk model①

Tian Dongping (田东平)

(*Institute of Computer Software, Baoji University of Arts and Sciences, Baoji 721007, P.R.China) (**Institute of Computational Information Science, Baoji University of Arts and Sciences, Baoji 721007, P.R.China)

Semantic image annotation based on GMM and random walk model①

Tian Dongping (田东平)②***

(*Institute of Computer Software, Baoji University of Arts and Sciences, Baoji 721007, P.R.China) (**Institute of Computational Information Science, Baoji University of Arts and Sciences, Baoji 721007, P.R.China)

Automatic image annotation has been an active topic of research in computer vision and pattern recognition for decades. A two stage automatic image annotation method based on Gaussian mixture model (GMM) and random walk model (abbreviated as GMM-RW) is presented. To start with, GMM fitted by the rival penalized expectation maximization (RPEM) algorithm is employed to estimate the posterior probabilities of each annotation keyword. Subsequently, a random walk process over the constructed label similarity graph is implemented to further mine the potential correlations of the candidate annotations so as to capture the refining results, which plays a crucial role in semantic based image retrieval. The contributions exhibited in this work are multifold. First, GMM is exploited to capture the initial semantic annotations, especially the RPEM algorithm is utilized to train the model that can determine the number of components in GMM automatically. Second, a label similarity graph is constructed by a weighted linear combination of label similarity and visual similarity of images associated with the corresponding labels, which is able to avoid the phenomena of polysemy and synonym efficiently during the image annotation process. Third, the random walk is implemented over the constructed label graph to further refine the candidate set of annotations generated by GMM. Conducted experiments on the standard Corel5k demonstrate that GMM-RW is significantly more effective than several state-of-the-arts regarding their effectiveness and efficiency in the task of automatic image annotation.

semantic image annotation, Gaussian mixture model (GMM), random walk, rival penalized expectation maximization (RPEM), image retrieval

0 Introduction

With the advent and popularity of world wide web, the number of accessible digital images for various purposes is growing at an exponential speed. To make the best use of these resources, people need an efficient and effective tool to manage them. In such context, content-based image retrieval (CBIR) was introduced in early 1990s, which heavily depends on the low-level features to find images relevant to the query concept that is represented by the query example provided by the user. However, in the field of computer vision and multimedia processing, the semantic gap between low-level visual features and high-level semantic concepts is a major obstacle to CBIR. As a result, automatic image annotation (AIA) has appeared and become an active topic of research in computer vision for decades due to its potentially large impact on both image understanding and web image search[1]. To be specific, AIA refers to a process to generate textual words automatically to describe the content of a given image, which plays a crucial role in semantic based image retrieval. As can be seen from the literature, the research on AIA has mainly proceeded along two categories. The first one poses image annotation as a supervised classification problem, which treats each semantic keyword or concept as an independent class and assigns each keyword or concept one classifier. More specifically, such kind of approaches predicts the annotations for a new image by computing the similarity at visual level and propagating corresponding keywords subsequently. Representative work includes automatic linguistic index for pictures[2]and supervised formulation for semantic image annotation and retrieval[3]. In contrast, the second category treats the words and visual tokens in each image as equivalent features in different modalities. Followed by image annotation is formalized via modeling the joint distribution of visual and textual features on the training data and predicting the missing textual features for a new image. Representative research includes translation model (TM)[4], cross-media relevance model (CMRM)[5], continuous space relevance model (CRM)[6], multiple Bernoulli relevance model (MBRM)[7], probabilistic latent semantic analysis (PLSA)[8]and correlated topic model[9], etc. By comparison, the former approach is relatively direct and natural to be understood. However, its performance is limited with the increase of the number of the semantic concepts and explosive multimedia data on the web. On the other hand, the latter often requires large-scale parameters to be estimated and the accuracy is strongly affected by the quantity and quality of the training data available.

The content of this paper is structured as follows. Section 1 summarizes the related work, particularly GMM applied in the fields of automatic image annotation and retrieval. Section 2 elaborates the proposed GMM-RW model, including its parameter estimation, label similarity graph and refining annotation based on the random walk. In Section 3, conducted experiments are reported and analyzed based on the standard Corel5k dataset. Finally, some concluding remarks and potential research directions of GMM in the future are given in Section 4.

1 Related work

Gaussian mixture model (GMM), as another kind of supervised learning method, has been extensively applied in machine learning and pattern recognition. As the representative work using GMM for automatic image annotation, Yang, et al.[10]formulate AIA as a supervised multi-class labeling problem. They employ color and texture features to form two separate vectors for which two independent Gaussian mixture models are estimated from the training set as the class densities by means of the EM algorithm in conjunction with a denoising technique. In Ref.[11], an effective visual vocabulary was constructed by applying hierarchical GMM instead of the traditional clustering methods. Meanwhile, PLSA was utilized to explore semantic aspects of visual concepts and to discover topic clusters among documents and visual words so that every image could be projected on to a lower dimensional topic space for more efficient annotation. Besides, Wang, et al.[12]adapted the conventional GMM to a global one estimated by all patches from training images along with an image-specific GMM obtained by adapting the mean vectors of the global GMM and retaining the mixture weights and covariance matrices. Afterwards GMM is embedded into the max-min posterior pseudo-probabilities for AIA, in which the concept-specific visual vocabularies are generated by assuming that the localized features of images with a specific concept satisfy the distribution of GMM[13]. It is generally believed that the spatial relation among objects is very important for image understanding and recognition. In more recent work[14], a new method for automatic image annotation based on GMM by region-based color and coordinate of matching is proposed to be taken into account this factor. To be specific, this method firstly partitions images into disjoint, connected regions with color features and x-y coordinate while a training dataset is modeled through GMM to have a stable annotation result in the later phase.

As the representative work for CBIR, Sahbi[15]proposed a GMM for clustering and its application to image retrieval. In particular, each cluster of data, modeled as a GMM into an input space, is interpreted as a hyperplane in a high dimensional mapping space where the underlying coefficients are found by solving a quadratic programming problem. In Ref.[16], GMM was leveraged to work on color histograms built with weights delivered by the bilateral filter scheme, which enabled the retrieval system not only to consider the global distribution of the color image pixels but also to take into account their spatial arrangement. In the work of Sayad, et al.[17], a new method was introduced by using multilayer PLSA for image retrieval, which could effectively eliminate the noisiest words generated by the vocabulary building process. Meanwhile, the edge context descriptor is extracted by GMM as well as a spatial weighting scheme is constructed based on GMM to reflect the information about the spatial structure of the images. At the same time, Raju, et al.[18]presented a method for CBIR by making use of the generalized GMM. Wan, et al.[19]proposed a clustering based indexing approach called GMM cluster forest to support multi-features based similarity search in high-dimensional spaces, etc. In addition, GMM has also been successfully applied in the task of other multimedia related fields[20-24].

As briefly reviewed above, most of these GMM related models can achieve encouraging performance and motivate us to explore better image annotation methods with the help of their excellent experiences and knowledge. So in this paper, a two stage automatic image annotation method is proposed based on Gaussian mixture model and random walk. First, GMM is learned by the rival penalized expectation maximization algorithm to estimate the posterior probabilities of each annotation keyword. In other words, GMM is exploited to capture the initial semantic annotations, which can be seen as the first stage of AIA. Second, a label similarity graph is constructed by a weighted linear combination of label similarity and visual similarity of images associated with the corresponding labels, which can efficiently avoid the phenomena of polysemy and synonym. Third, the random walk is implemented over the constructed label graph to further refine the candidate set of annotations generated by GMM, which can be viewed as the second stage of image annotation. At length, extensive experiments on Corel5k dataset validate the effectiveness and efficiency of the proposed model.

2 Proposed GMM-RW

In this section, the scheme of the GMM-RW model proposed in this study is first described (as depicted in Fig.1). Subsequently, GMM-RW is elaborated from three aspects of GMM and its parameter estimation, construction of the label similarity graph and refining annotation based on the random walk, respectively.

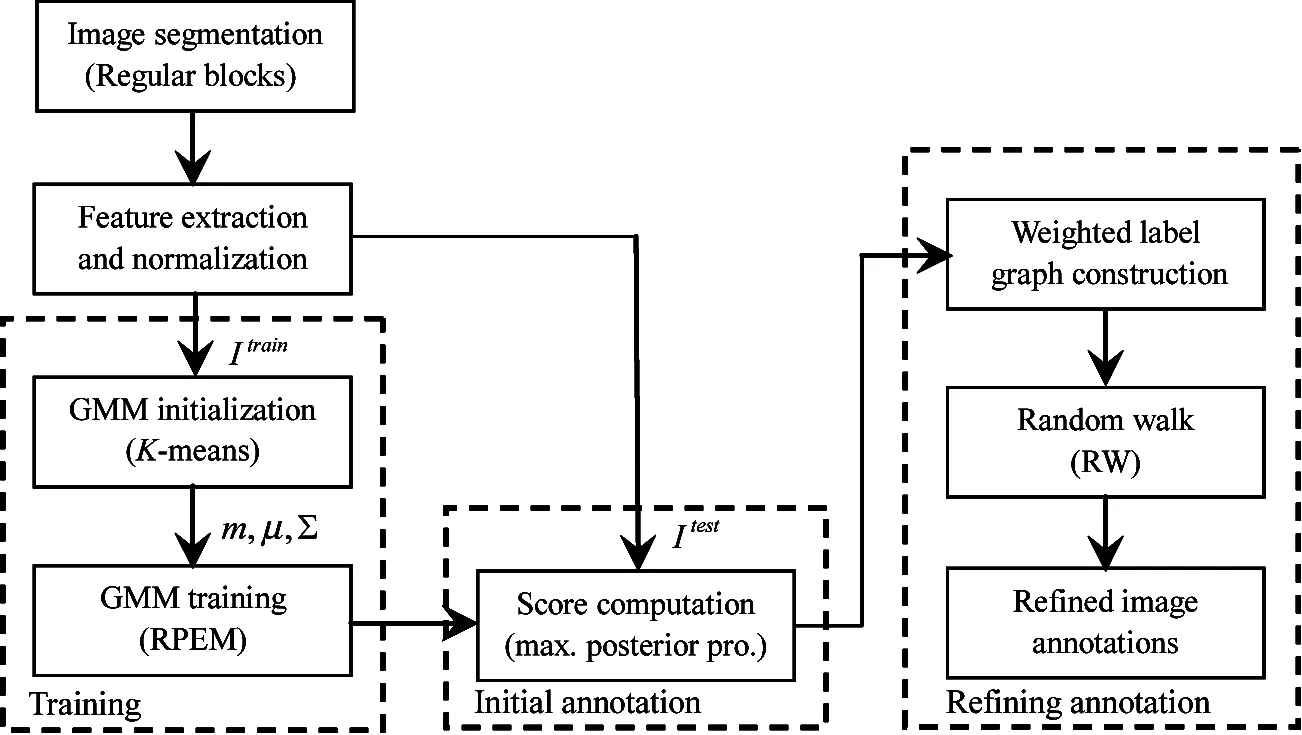
Fig.1 Scheme of the proposed GMM-RW model

2.1 GMM and its parameter estimation

A Gaussian mixture model is a parametric probability density function represented as a weighted sum of Gaussian component densities. GMM is commonly used as a parametric model of the probability distribution of continuous measurements. More formally, a GMM is a weighted sum ofMcomponent Gaussian densities as given by the following equation.

(1)

where x is aD-dimensional continuous-valued data vector,wi(i=1,2,…,M) denotes the mixture weights,g(x|μi, ∑i),i=1,2,…,M, are the component Gaussian densities. Each component density is aD-variate Gaussian function as follows.

g(x|μi,Σi)=

(2)

withmeanvectorμiand covariance matrix Σi. The mixture weights satisfy the constraint, i.e., sum to 1. The complete GMM is parameterized by the mean vectors, covariance matrices and mixture weights from all the component densities, and these parameters can be collectively represented by the notationλ={wi,μi, Σi},i=1, 2,…,M.

There are several techniques available for estimating parameters of GMM. By far the most popular and well-established method is the maximum likelihood (ML) estimation, whose aim is to find the model parameters to maximize the likelihood of the GMM given the training data. But in general, the expectation-maximization (EM) algorithm is employed to fit GMM due to the infeasibility of direct maximization for ML. However, there is no penalty for the redundant mixture components based on the EM, which means that the number of components in a GMM cannot be automatically determined and has to be assigned in advance. To this end, the rival penalized expectation maximization (RPEM) algorithm[25]is leveraged to determine the number of components as well as to estimate the model parameters. Since RPEM introduces unequal weights into the conventional likelihood, the weighted likelihood can be written as below:

(3)

with

(4)

whereh(j|xi,λ)=ωjp(xi|μj, ∑j)/p(xi|λ) is the posterior probability thatxibelongs to thej-th component in the mixture,λis a positive constant,g(j|xi,λ),j=1,2,…,M, are designable weight functions, satisfying the following constraints:

(5)

In literature[24], they are constructed as follows:

g(j|xi,λ)=(1+εi)I(j|xi,λ)-εih(j|xi,λ)

(6)

whereI(j|xi,λ) equals to 1 ifj=argmax1≤i≤Mh(i|x,λ) and 0 otherwise.εiis a small positive quantity. The major steps of RPEM algorithm can be summarized as below:

Algorithm1：TheRPEMalgorithmforGMMmodelingInput：featurevectorx，M，thelearningrateη，themaximumnumberofepochsepochmax，initializeλasλ(0)．Process：1． epochcount=0，m=0；2． whileepochcount≤epochmax，do3． fori=1toNdo4． Givenλ(m)，calculateh(j|xi，λ(m))toobtaing(j|xi，λ(m))byEq．(6)．5． λ(m+1)=λ(m)+Δλ=λ(m)+η∂l(xi；λ)∂λλ(m)，6． m=m+1．7． endfor8． epochcount=epochcount+1；9． endwhileOutput：theconvergedλforGMM．

Based on Gaussian mixture model and RPEM algorithm described above, GMM can be trained and utilized to characterize the semantic model of the given concepts by Eq.(1). Assume that the training image is represented by both a visual featureX={x1,x2,…,xm} and a keyword listW={w1,w2,…,wn}, wherexi(i=1,2,…,m) denotes the visual feature for regioniandwj(j=1,2,…,n) is thej-th keyword in the annotation. For a test imageIrepresented by its visual feature vector X={x1,x2,…,xm}, according to Bayesian rule, the posterior probabilityp(wi|I) can be calculated based on the conditional probabilityp(I|wi) and prior probabilityp(wi) as follows:

(7)

From Eq.(7), the topnkeywords can be selected as the initial annotations for image X.

2.2 Construction of the label similarity graph

In the process of automatic image annotation, at least three kinds of relations are involved based on two different modal data. That is, image-to-image, image-to-word and word-to-word relations. How to reasonably reflect these cross-modal relations between images and words plays a critical role in the task of AIA. Note that the most common approaches include WordNet[26]and normalized Google distance (NGD)[27]. From their definitions, it can be easily observed that NGD is actually a measure of the contextual relation while WordNet focuses on the semantic meaning of the keyword itself. Moreover, both of them build word correlations only based on the textual descriptions whereas the visual information of images in the dataset is not considered at all, which can easily lead to the phenomenon that different images with the same candidate annotations would obtain the same annotation results after the refined process. For this reason, an effective pairwise similarity strategy is devised by calculating a weighted linear combination of label similarity and visual similarity of images associated with the corresponding labels, in which the label similarity between wordswiandwjis defined as

sl(wi,wj)=exp(-d(wi,wj))

(8)

whered(wi,wj) represents the distance between two wordswiandwjand it is defined similarly to NGD as below:

(9)

wheref(wi) andf(wj) denote the numbers of images containing wordswiandwjrespectively,f(wi,wj) is the number of images containing bothwiandwj,Gis the total number of images in the dataset.

Similar to Ref.[28], for labelwassociated with imagex, the nearest neighbors ofKarecollectedfromimagescontainingw, and these images can be regarded as the exemplars of labelwwith respect tox. Thus from the point view of labels associated with an image, the visual similarity between labelswiandwjis given as follows:

(10)

whereΓwis the representative image collection of wordw,xandydenote image features corresponding to the respective image collections of wordswiandwj,σis the user-defined radius parameter for the Gaussian kernel function. To benefit from each other of the two similarities described above, a weighted linear combination of label similarity and visual similarity is defined as below:

sij=s(wi,wj) =λsl(wi,wj)+(1-λ)sv(wi,wj)

(11)

whereλ∈[0,1] is utilized to control the weights for each measurement.

2.3 Refining annotation based on random walk

In the following, the refining image annotation stage is to be elaborated based on the initial annotations generated by GMM and the random walk model. Given that a label graph constructed in subsection 2.2 withnnodes,rk(i) is used to denote the relevance score of nodeiat iterationk,Pdenotes an-by-ntransition matrix, whose elementpijindicates the probability of the transition from nodeito nodejand it is computed as

(12)

wheresijis the pairwise label similarity (defined by Eq.(11)) between nodeiand nodej. Then the random walk process can be formulated as

(13)

whereα∈(0,1) is a weight parameter to be determined,vjdenotes the initial annotation probabilistic scores calculated by the GMM. In the process of refining image annotation, random walk proceeds until it reaches the steady-state probability distribution and subsequently the top several candidates with the highest probabilities can be seen as the final refining image annotation results.

3 Experimental results and analysis

3.1 Dataset and evaluation measures

The proposed GMM-RW is tested on the Corel5k image dataset obtained from the literature[4]. Corel5k consists of 5,000 images from 50 Corel Stock Photo CD’s. Each CD contains 100 images with a certain theme (e.g. polar bears), of which 90 are designated to be in the training set and 10 in the test set, resulting in 4,500 training images and a balanced 500-image test collection. Alternatively, for the sake of fair comparison, similar features to Ref.[7] are extracted. First of all, images are simply decompose into a set of 32×32-sized blocks, followed by computing a 36-dim feature vector for each block, consisting of 24 color features (auto-correlogram) computed over 8 quantized colors and 3 manhattan distances, 12 texture features (Gabor filter) computed over 3 scales and 4 orientations. As a result, each block is represented as a 36-dim feature vector. Finally, each image is represented as a bag of features, i.e., a set of 36 dimensional vectors. And these features are subsequently employed to train GMM based on the RPEM algorithm. In addition, the value ofλin Eq.(11) is set to be 0.6, and the value ofαin Eq.(13) is set to be 0.5 by trial and error. Without loss of generality, the commonly used metrics precision and recall of every word in the test set are calculated and the mean of these values is utilized to summarize the performance.

3.2 Results of automatic image annotation

Matlab 7.0 is applied to implement the proposed GMM-RW model. Specifically, the experiments are carried out on a 1.80GHz Intel Core Duo CPU personal computer (PC) with 2.0G memory running Microsoft windows xp professional. To verify the effectiveness of the proposed model, it is compared with several previous approaches[4-8]. Table 1 reports the experimental results based on two sets of words: the subset of 49 best words and the complete set of all 260 words occur in the training set. From Table 1, it is clear that the model markedly outperforms all the others, especially the first three approaches. Meanwhile, it is also superior to PLSA-WORDS and MBRM by the gains of 21 and 4 words with non-zero recall, 30% and 4% mean per-word recall in conjunction with 79% and 4% mean per-word precision on the set of 260 words respectively. In addition, compared to MBRM on the set of 49 best words, improvement can be get in mean per-word precision despite the mean per-word recall of GMM-RW is the same as that of MBRM.

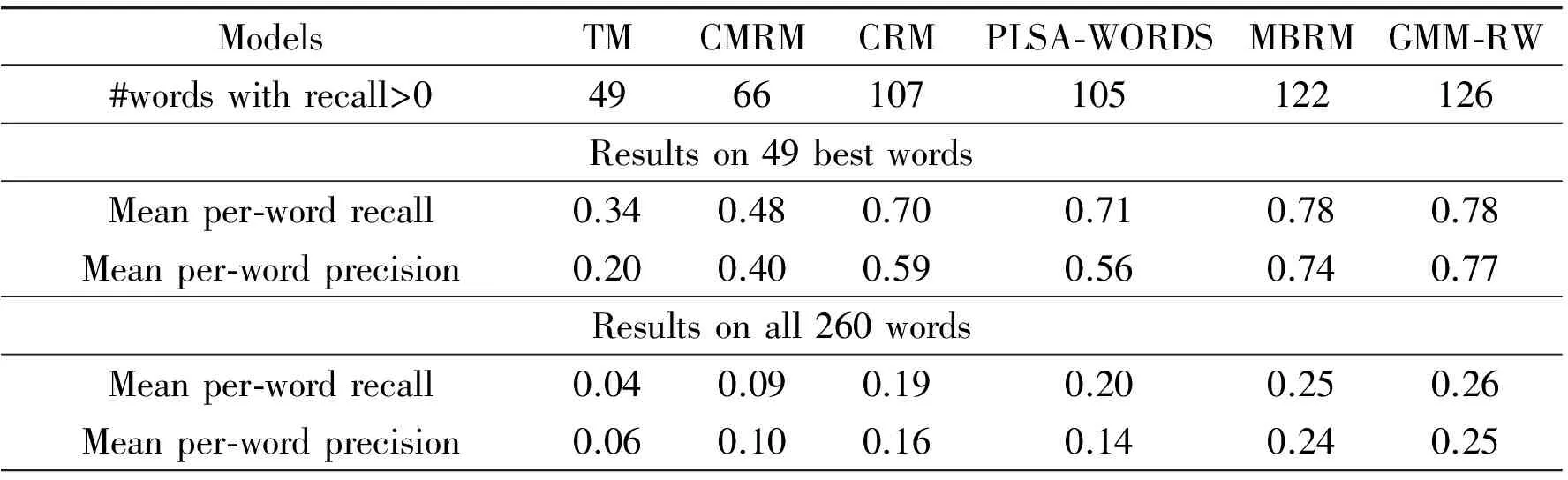
Table 1 Performance comparison on Corel5k dataset

To further illustrate the effect of GMM-RW model for automatic image annotation, Fig.2 displays the average annotation precision of the selected 10 words “flowers”, “mountain”, “snow”, “tree”, “building”, “beach”, “water”, “sky”, “bear” and “cat” based on GMM and GMM-RW models, respectively. As shown in Fig.2, the average precision of the model is obviously higher than that of GMM. The reason lies in that in addition to profit from the calculation strategy of cross-modal relations between images and words. GMM-RW, to a large extent, takes benefit from the random walk process to further mine the correlation of the candidate annotations.

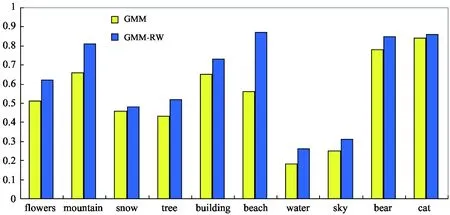
Fig.2 Average precision based on GMM and GMM-RW

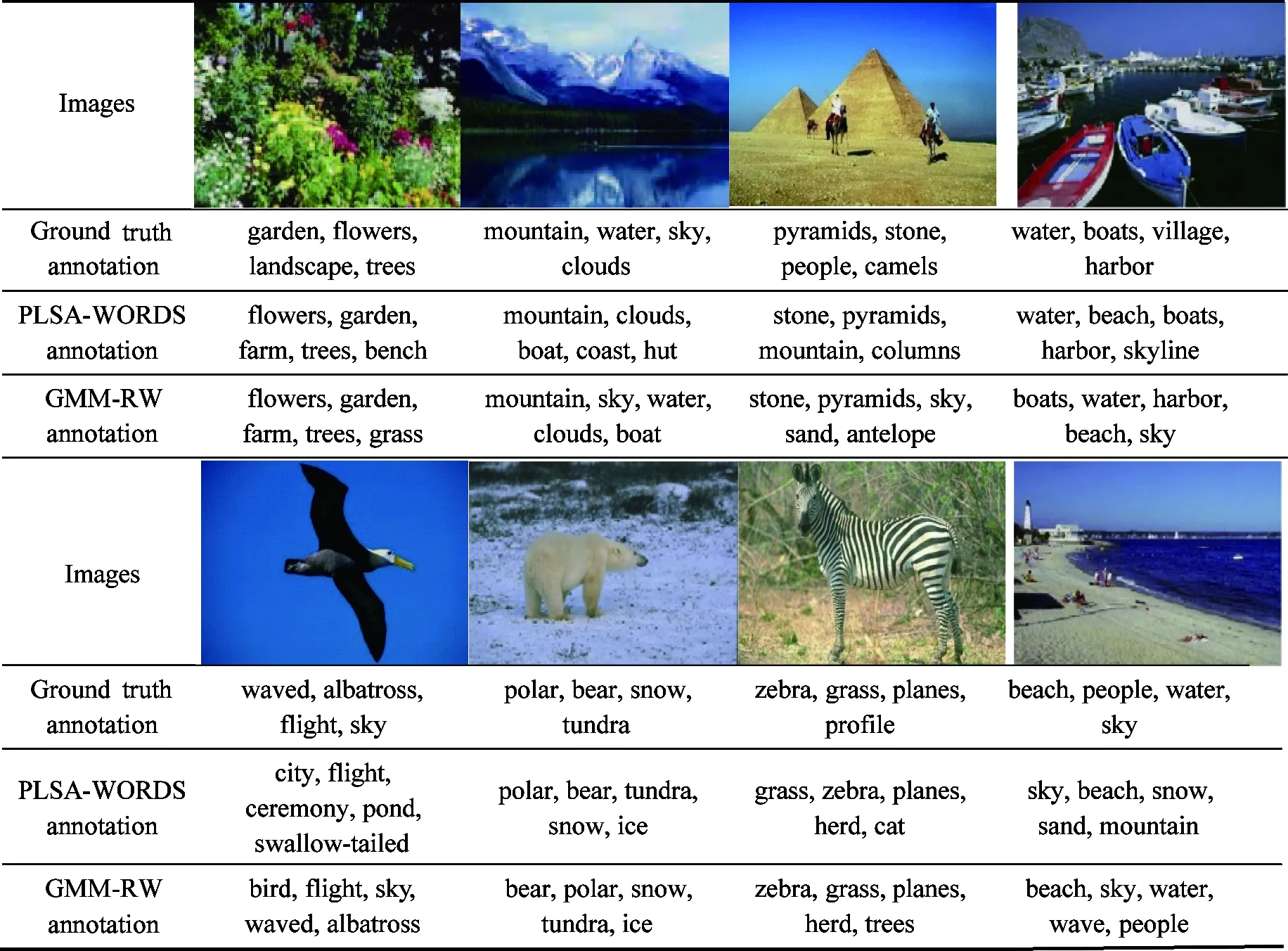
Alternatively, Table 2 shows some examples of image annotation (only eight cases are listed here due to the limited space) produced by PLSA-WORDS and GMM-RW, respectively. It is clearly observed that the model is able to generate more accurate annotation results compared with the original annotations as well as the ones provided in Ref.[8]. Taking the first image in the first row for example, there exist four tags in the original annotation. However, after annotation by GMM-RW, its annotation is enriched by the other keyword “grass”, which is very appropriate and reasonable to describe the visual content of the image. On the other side, it is important to note that the annotation ranking of the keywords compared to that generated by the PLSA-WORDS is more reasonable, which plays a crucial role in semantic based image retrieval. In addition, as for the complexity of GMM-RW, assuming that there areDtraining images and each image producesRvisual feature vectors, then the complexity of our model isO(DR), which is similar to the classic CRM and MBRM models mentioned in Ref.[3].

Table 2 Annotation comparison with PLSA-WORDS and GMM-RW

4 Conclusions and future work

In this paper, a two stage automatic image annotation method is presented based on GMM and a random walk model. First of all, GMM fitted by the rival penalized expectation maximization is applied to estimate the posterior probabilities of each annotation keyword. Followed by a random walk process over the constructed label similarity graph is implemented to further mine the correlation of the candidate annotations so as to capture the refining results. Particularly, the label similarity graph is constructed by a weighted linear combination of label similarity and visual similarity of images associated with the corresponding labels, which can efficiently avoid the phenomena of polysemy and synonym in the course of automatic image annotation. Extensive experiments on the general-purpose Corel5k dataset validate the feasibility and utility of the proposed GMM-RW model.

As for future work, a plan is made to explore more powerful GMM related models for automatic image annotation from the following aspects. First, due to the classic GMM has limitation in its modeling abilities as all data points of an object are required to be generated from a pool of mixtures with the same set of mixture weights, so how to determine the weight factors of GMM more appropriately is well worth exploring. Second, how to speed up the GMM estimation with EM algorithm is also an important work for large-scale multimedia processing. In other words, the choice of alternate estimation techniques for the estimation of GMM parameters could also be very valuable. Third, how to introduce semi-supervised learning into the proposed approach to utilize the labeled and unlabeled data simultaneously is a worthy research direction. At the same time, work on web image annotation is continued by refining more relevant semantic information from web pages and building more suitable connection between image content features and available semantic information. Last but not the least, GMM-RW should be expected to be applied in more wider ranges to deal with more multimedia related tasks, such as speech recognition, video recognition and other multimedia event detection tasks, etc.

[ 1] Tian D P. Exploiting PLSA model and conditional random field for refining image annotation.HighTechnologyLetters, 2015,21(1):78-84

[ 2] Li J, Wang J. Automatic linguistic indexing of pictures by a statistical modeling approach.IEEETransactionsonPatternAnalysisandMachineIntelligence, 2003,25(19):1075-1088

[ 3] Carneiro G, Chan A, Moreno P, et al. Supervised learning of semantic classes for image annotation and retrieval.IEEETransactionsonPatternAnalysisandMachineIntelligence, 2007,29(3):394-410

[ 4] Duygulu P, Barnard K, Freitas N De, et al. Object recognition as machine translation: learning a lexicon for a fixed image vocabulary. In: Proceedings of the 7th European Conference on Computer Vision, Copenhagen, Denmark, 2002. 97-112

[ 5] Jeon L, Lavrenko V, Manmantha R. Automatic image annotation and retrieval using cross-media relevance models. In: Proceedings of the 26th International ACM SIGIR Conference on Research and Development in Information Retrieval, Toronto, Canada, 2003. 119-126

[ 6] Lavrenko V, Manmatha R, Jeon J. A model for learning the semantics of pictures. In: Proceedings of the Advances in Neural Information Processing Systems 16, Vancouver, Canada, 2003. 553-560

[ 7] Feng S, Manmatha R, Lavrenko V. Multiple Bernoulli relevance models for image and video annotation. In: Proceedings of the International Conference on Computer Vision and Pattern Recognition, Washington, USA, 2004. 1002-1009

[ 8] Monay F, Gatica-Perez D. Modeling semantic aspects for cross-media image indexing.IEEETransactionsonPatternAnalysisandMachineIntelligence, 2007,29(10):1802-1817

[ 9] Blei D, Lafferty J. Correlated topic models.AnnalsofAppliedStatistics, 2007,1(1):17-35

[10] Yang F, Shi F, Wang Z. An improved GMM-based method for supervised semantic image annotation. In: Proceedings of the International Conference on Intelligent Computing and Intelligent Systems, Shanghai, China, 2009. 506-510

[11] Wang Z, Yi H, Wang J, et al. Hierarchical Gaussian mixture model for image annotation via PLSA. In: Proceedings of the 5th International Conference on Image and Graphics, Xi’an, China, 2009. 384-389

[12] Wang C, Yan S, Zhang L, et al. Multi-label sparse coding for automatic image annotation. In: Proceedings of the International Conference on Computer Vision and Pattern Recognition, Miami, USA, 2009. 1643-1650

[13] Wang Y, Liu X, Jia Y. Automatic image annotation with cooperation of concept-specific and universal visual vocabularies. In: Proceedings of the 16th International Conference on Multimedia Modeling, Chongqing, China, 2010. 262-272

[14] Luo X, Kita K. Region-based image annotation using Gaussian mixture model. In: Proceedings of the 2nd International Conference on Information Technology and Software Engineering, Beijing, China, 2013. 503-510

[15] Sahbi H. A particular Gaussian mixture model for clustering and its application to image retrieval.SoftComputing, 2008, 12(7):667-676

[16] Luszczkiewicz M, Smolka B. Application of bilateral filtering and Gaussian mixture modeling for the retrieval of paintings. In: Proceedings of the 16th International Conference on Image Processing, Cairo, Egypt, 2009. 77-80

[17] Sayad I, Martinet J, Urruty T, et al. Toward a higher-level visual representation for content-based image retrieval.MultimediaToolsandApplications, 2012,60(2):455-482

[18] Raju L, Vasantha K, Srinivas Y. Content based image retrievals based on generalization of GMM.InternationalJournalofComputerScienceandInformationTechnologies, 2012,3(6): 5326-5330

[19] Wan Y, Liu X, Tong K, et al. GMM-ClusterForest: a novel indexing approach for multi-features based similarity search in high-dimensional spaces. In: Proceedings of the 19th International Conference on Neural Information Processing, Doha, Qatar, 2012. 210-217

[20] Dixit M, Rasiwasia N, Vasconcelos N. Adapted Gaussian models for image classification. In: Proceedings of the International Conference on Computer Vision and Pattern Recognition, Providence, USA, 2011. 937-943

[21] Celik T. Image change detection using Gaussian mixture model and genetic algorithm.JournalofVisualCommunicationandImageRepresentation, 2010,21(8):965-974

[22] Beecks C, Ivanescu A, Kirchhoff S, et al. Modeling image similarity by Gaussian mixture models and the signature quadratic form distance. In: Proceedings of the 13th International Conference on Computer Vision, Barcelona, Spain, 2011. 1754-1761

[23] Wang Y, Chen W, Zhang J, et al. Efficient volume exploration using the Gaussian mixture model.IEEETransactionsonVisualizationandComputerGraphics, 2011,17(11):1560-1573

[24] Inoue N, Shinoda K. A fast and accurate video semantic-indexing system using fast MAP adaptation and GMM super-vectors.IEEETransactionsonMultimedia, 2012,14(4):1196-1205

[25] Cheung Y. Maximum weighted likelihood via rival penalized EM for density mixture clustering with automatic model selection.IEEETransactionsonKnowledgeandDataEngineering, 2005,17(6):750-761

[26] Fellbaum C. WordNet. Theory and Applications of Ontology: Computer Applications, 2010. 231-243

[27] Cilibrasi R, Paul M. The Google similarity distance.IEEETransactionsonKnowledgeandDataEngineering, 2007, 19(3):370-383

[28] Liu D, Hua X, Yang L, et al. Tag ranking. In: Proceedings of the 18th International Conference on World Wide Web, Madrid, Spain, 2009. 351-360

10.3772/j.issn.1006-6748.2017.02.015

①Supported by the National Basic Research Program of China (No.2013CB329502), the National Natural Science Foundation of China (No.61202212), the Special Research Project of the Educational Department of Shaanxi Province of China (No.15JK1038) and the Key Research Project of Baoji University of Arts and Sciences (No.ZK16047).

②To whom correspondence should be addressed. E-mail: tdp211@163.com

on May 25， 2016

ping, born in 1981. He received his M.Sc. and Ph.D. degrees in computer science from Shanghai Normal University and Institute of Computing Technology, Chinese Academy of Sciences in 2007 and 2014, respectively. His research interests include computer vision, machine learning and evolutionary computation.