Bloch空间上一类特殊复合算子的上界估计

胡 蓉，张 瑞

(四川文理学院 数学与财经系，四川 达州 635000)

Bloch空间上一类特殊复合算子的上界估计

胡 蓉，张 瑞

(四川文理学院 数学与财经系，四川 达州 635000)

介绍了定义在单位多圆柱上的Bloch空间中的一类特殊复合算子，根据Bergman度量的定义，计算由该类特殊复合算子中的复合函数所决定的Bergman度量，得到其满足的特殊性质，最后利用该性质得到该类特殊复合算子在Bloch空间上的上界估计．

单位多圆柱；Bloch空间；复合算子；Bergman度量

0 引言

早在上个世纪，就有不少学者开始研究复合算子及其相关性质，在单复变中，这方面的研究已取得了较好的成果．于是，越来越多的学者开始研究多复变中复合算子的相关问题，虽然到目前为止已经有了一些优美的结果，[1-4]但仍有很多问题诸如常见空间上复合算子的有界性和紧性等依然是人们研究的重点和难点.本文将对定义在多圆柱上的Bloch空间上的某类比较特殊的复合算子做出研究，说明这类复合算子的有界性并进一步得到它的上界估计.该结论将会为定义在多圆柱上Bloch空间上的对偶Hausdorff算子有界性的研究奠定一定的基础.

1 预备知识

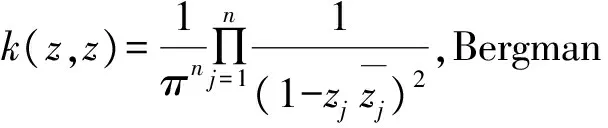
任意f∈H(Un)，记

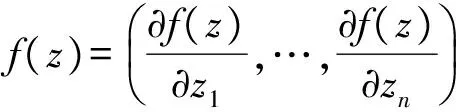
定义1 设f∈H(Un),若f满足sup{Qf(z)|z∈Un}lt;∞,则称f为Un上的Bloch函数.[7]

记‖f‖B=sup{Qf(z)|z∈Un},称其为Un上的Bloch范数.由Bloch函数全体所构成的空间成为Bloch空间，记为B(Un).

引理1Ω为Cn中的齐性有界域，Hz(u,u)为Bergman度量，对∀f∈H(Ω)，存在常数C使得

2 主要结果

∀f∈B(Un)，记复合算子

Ut(f)(z)=f(Ψt1(z1),ψt2(z2)，…，ψtn(zn))=fψt(z),其中ψt(z)=(ψt1(z1),ψt2(z2),…，ψtn(zn)),ψti(zi)=tizi+1-ti(ti∈(0,1),i=1,2,…,n)为单位圆盘U→U的全纯函数．

定理1 单位多圆柱Un是Cn中的有界Bergman域．特别地，对上述ψt，有

Hψt(z)(Jψt(z)u,Jψt(z)u)≤CtHz(u,u),

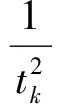
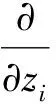
从而

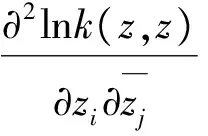
则

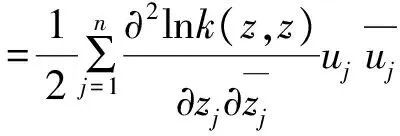
另一方面，

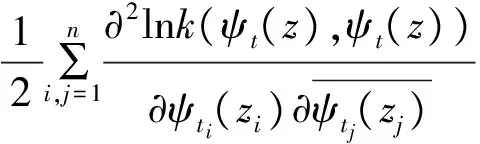
而

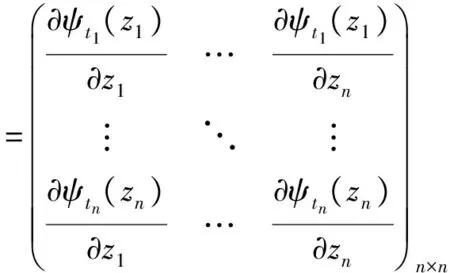
则

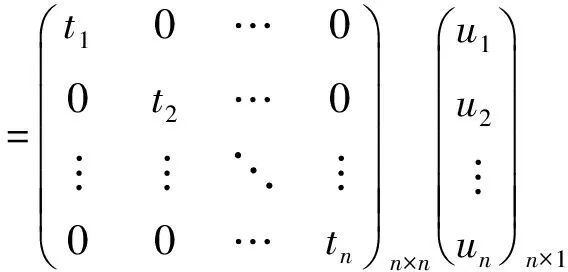
=(t1u1,t2u2，…，tnun)T.

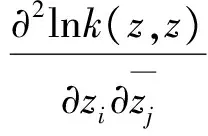
从而

又因为

|ψtj(zj)|2=|tjzj+1-tj|2≤(tj|zj|+(1-tj))2

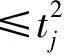
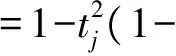
因此

定理2 复合算子Ut(f)(z)在B(Un)上有界，且

证明：∀f∈B(Un),φ∈H(Un)，由链式法则，复梯度

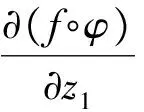
∀u∈Cn-{0}，若Jφ(z)u=0，则▽(f∘φ)(z)u=0;若Jφ(z)u≠0,则

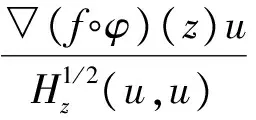
从而

由定理1，对ψt有

故

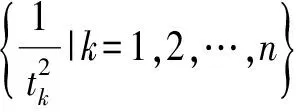
即

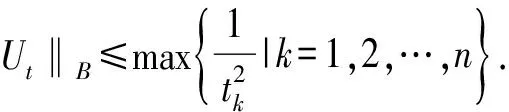
[1] Hyungwoon K,Michael S,Kehe Z.CompositionOperatorsonthePolydiscInducedbySmoothSymbols[J].Journal of Functional Analysis,2008(254):2911-2925.

[2] Steven G K.FunctionTheoryofSeveralComplexVariables[M].Rhode Island:AMS Chelsea Publishing,2000:41-58.

[3] LU Yu-feng.CompactOperatorsontheBergmanSpacesoftheUnitBallandthePolydiskinCn[J].Northeast Math J，2000(16):347-356.

[4] 胡 蓉.多圆柱上的Bloch空间及其函数模的上界估计新证[J].内江师范学院学报，2011(4):18-20.

[5] 史济怀.多复变函数论基础[M].北京：高等教育出版社，1996：144-165.

[6] Kehe Z.SpacesofHolomorphicFunctionsintheUnitBall[M].Berlin:Springer-Verlag,2004:76-78.

[7] Timoney R.BlochFunctionsinSeveralComplexVariablesⅠ[J].Bull London Math Soc,1980(12):241-267.

[8] Zhou Ze-hua, Shi Ji-huai.CompositionOperatorsontheBlochSpaceinPolydiscs[J].Overseas Publishers Association,2001(46):73-88.

[责任编辑邓杰]

TheUpperBoundofaSpecialClassofCompositionOperatorsontheBlochSpace

HU Rong, ZHANG Rui

(Mathematics and Finance-Economics Department of Sichuan University of Arts and Science, Dazhou Sichuan 635000, China)

Introduce the special class of composite operators on the Bloch Space in unit poly-disk, according to the definition of Bergman metric to calculate the Bergman metric of the composite function determined by the special composite operators, and get the inequality, then use the inequality to get the upper bound of the special composition operators on the Bloch spaces.

unit polydisk; bloch space; composition operators; Bergman metric

2011-11-17

胡 蓉(1985—)，女，四川南充人.讲师，硕士，主要从事多复变函数论研究.

O174.56

A

1674-5248(2013)02-0017-03