Hilbert空间中平衡问题变分不等式问题和可数族k-严格伪压缩映像的强收敛定理

冯仁勇,何中全

(西华师范大学 数学与信息学院,四川 南充 637002)

Hilbert空间中平衡问题变分不等式问题和可数族k-严格伪压缩映像的强收敛定理

冯仁勇,何中全

(西华师范大学 数学与信息学院,四川 南充 637002)

在Hilbert空间中引进一种新的迭代算法,得到了一类平衡问题变分不等式问题和可数族k-严格伪压缩映像的强收敛定理,所得结果改进并推广了这类问题最新的一些结论.

平衡问题;k-Hilbert空间;k-严格伪压缩映像;迭代算法

0 引言

设H是一实的Hilbert空间,C是H的一非空闭凸子集.对于任意的x∈H,存在唯一xC∈C使得‖x-xC‖≤‖x-y‖,∀y∈C.令Px=xC,称P为H到C上的投影映射.记T的不动点集为F(T).称映像T:C→C是k-严格伪压缩映像,如果

‖Tx-Ty‖2≤‖x-y‖2+k‖(I-T)x-(I-T)y‖2,k∈[0,1),∀x,y∈C.

A∶C→H，变分不等式问题(VI)是求z∈C,使得lt;Az,y-zgt;≥0,∀y∈C.此变分不等式问题的解集用Ⅵ(C,A)表示.称映像A∶C→H为α-逆强单调的,如果存在正数agt;0,使得lt;Ax-Ay,x-ygt;≥α‖Ax-Ay‖2,∀x,y∈C.

设φ(x,y):C×C→R是平衡函数,即每一个u∈C,φ(x,y)=0.考虑如下平衡问题(EP)：寻找z∈C,使得φ(z,y)≥0,∀y∈C.记它的解为EP.平衡问题包含了不动点问题、最优化问题、变分不等式问题、Nash平衡问题等.[1-5]

2008年,Chang[6]等介绍了如下迭代序列:

(1)

其中映像{Wn}是由一族非扩张映像{Sn}生成的.

在Hilbert空间中,关于寻求平衡问题的解集与不动点的解集的公共点问题,已有许多人研究 ，受文献[6]启发,本文在Hilbert空间中介绍了一个新的迭代序列,借以寻找平衡问题不动点问题和可数族k-严格伪压缩映像的公共不动点,并在适当的条件下得到了强收敛定理.本文的结果推广和改进了Chang 等人的相应结果.[7]

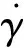
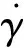
引理1[7]设{Si:C→C}是一有限族的非扩张映像,且{un}是对任意i≥1都有0≤uilt;1的非负实数序列,定义一个映射Wn∶C→C如下:

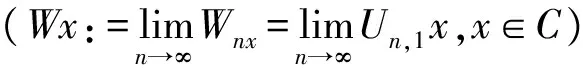
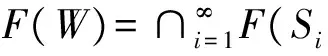
引理2[7]假设H为实Hilbert空间,C为H的非空闭凸子集,φ:C×C→R是一二元函数满足条件：

(A1)φ(x,x)=0,∀x∈C;

(A2)φ是单调的，即φ(x,y)+φ(y,x)≤0,∀x,y∀C;

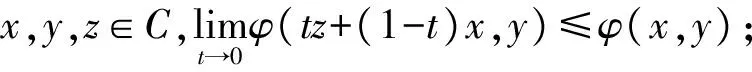
(A4)对每一x∈C,y→φ(x,y)是凸的和下半连续的.

这里{Wn:C→C}，按引理(2)，{αn}，{βn},{γn}⊂[0,1],λn⊂[0,1],{λn}⊂(0,2a),{rn}⊂[0,∞]，如果满足下列条件:

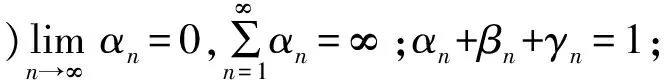
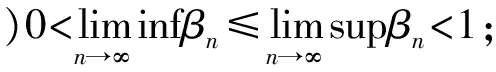
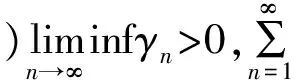
则{xn}和{un}强收敛于PF∩VI(C,A)∩EP(φ)(z) .

1 主要结果

定理1 设H为实Hilbert空间,C为H的非空闭凸子集,φ∶C×C→R是一二元函数且满足引理2中条件(A1)-(A4).

(3)

这里{Wn∶C→C}，按引理1，{αn},{βn},{γn}⊂[0,1],{λn}⊂(0,2α),{rn}⊂[0,∞],如果满足条件:

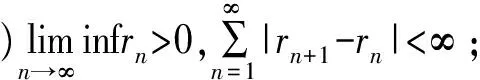
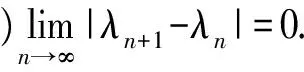
则{xn}和{un}强收敛于PF∩Ⅵ(C,A)∩EP(φ)(I-B+γf)(z).

证明:我们分三步证明该定理.

(1)证明Ti(∀i∈N+)是半闭的.设任意序列{zn}⊂D(Ti),zn→z(n→∞)∈D(Ti),且Tizn→P·‖Tiz-p‖=‖Tiz-Tizn+Tizn-p‖≤‖Tiz-Tizn‖+‖Tizn-p‖,由k-严格伪压缩映像的定义，存在ki∈[0,1),使得‖Tizn-Tiz‖2≤‖zn-z‖2+ki(‖zn-z‖2+‖Tizn-Tiz‖2).所以(1-ki)‖Tizn-Tiz‖2≤(1+ki)‖zn-z‖2,‖Tizn-Tiz‖2→0,(n→∞).故Ti(∀i∈N+) 是半闭的.

(2)证明F是闭凸集.只需证明F(Ti)(∀i∈N+)是闭凸集.设任意序列{zn}⊂F(Ti)，且zn→p·‖Tip-p‖=‖Tip-zn+zn-p‖≤‖Tip-zn‖+‖zn-p‖,根据k-严格伪压缩映像的定义,由(1)知‖Tizn-Tp‖→0,(n→∞).又Ti(∀i∈N+) 是半闭的.于是‖Tip-p‖=0,因此F(Ti) 是闭集.设p1和p2是F(Ti)中任意两点,由严格伪压缩映像定义知

‖TiP-p‖2=‖λ(Tip-p1)+(1-λ)(Tip-p2)‖

=λ‖Tip-p1‖2+(1-λ)‖Tip-p2‖2-λ(1-λ)‖p1-p2‖2

≤λ(‖p-p1‖2+ki‖Tip-p‖2)-(1-λ)(‖p2-p2‖2+ki‖Tip-p‖2)-λ(1-λ)‖p1-p2‖2=λ(1-λ)‖p1-p2‖2+ki‖Tip-p‖2，

所以(1-ki)‖Tip-p‖≤λ(1-λ)‖p1-p2‖2.

由ki∈[0,1] ，令T→0 ,得(1-ki)‖Tip-p‖2=0.

(3)证明Six=ξix-(1-ξi)Tix,ξi∈[ki,1) 是非扩张映像,且F(Si)=F(Ti).

‖Six-Siy‖2=‖ξi(x-y)+(1-ξi)(Tix-Tiy)‖2-ξi(1-ξi)‖((I-Ti)x-(I-Ti)y)‖

因为Ti(∀i∈N+) 是严格伪压缩映像,从而

‖Tix-Tiy‖2=‖x-y‖2+ki‖((I-Ti)x-(I-Ti)y)‖2.

于是有

‖Six-Siy‖2≤ξi‖x-y‖2+(1-ξi)‖x-y‖2-(1-ξi)(ξi-ki)‖(I-Ti)x-(I-Ti)y‖2=‖x-y‖2-(1-ξi)(ξi-ki)‖(I-Ti)x-(I-Ti)y‖2≤‖x-y‖2，

所以Si是非扩张映像,由Six=ξix-(1-ξi)Tix得x-Six=(1-ξi)(x-Tix).

因此F(Si)=F(Ti).由引理2知{xn}和{un}强收敛于PF∩Ⅵ(C,A)∩EP(φ)(I-B+γf)(z) .

[1] Rockafellar R T.OntheMaximalityofSumsofNonlinearMonotoneOperator[J].Trans Amer Math Soc,1970(149):75-88.

[2] Rockafellar R T.MonotoneOperatorsandProximalPointAlgorithm[J].SIAMJ Control Pptim,1976(14):877-898.

[3] Xu H K.IterativeAlgorithmforNonlinearMonotoneOperators[J].Math Soc，2002(66):240-256.

[4] Flam S D, Antipin A S.EquilibriumProgrammingUsingProximal-likeAlgorithms[J].Math Program,1997(78):29-41.

[5] Zhang S S, Rao R F, Hung J L.StrongConvergenceTheoremforaGeneralizedEquilibriumProblemandak-strictPseudocontractioninHilbertSpace[J].Appl Math Mech,2009(6):685-694.

[6] Liu M, Zhang S S.ANewIterativeMethodforFindingCommonSolutionsofGeneralizedEquilibriumProblem,FixedPointProblemOfInfinitek-strictPseudo-contractiveMappingsandQuasi-variationalInclusionProblem[J].Acta Mathematica Scientia，2012(2):499-519.

[7] Zhang S S, Joseph L H W, Chi K C.ANewMethodforSolvingEquilibriumProblemFixedPointProblemandVariationalInequalitiyProblemwithApplicationtoOptimization[J].Nonlinear Analysis,2009(9):3307-3319.

[责任编辑邓杰]

Kewwords:equilibrium problem; Hilbert space;k-strict pseudo-contraction mappings; iterative algorithm

VariationInequalitiesProblemsofEquilibriumProblemsandStrongConvergenceTheoremofaCountableFamilyofk-StrictPseudo-contractionMappinginHilbertSpace

FENG Reng-yong, HE Zhong-quan

(Mathematics and Information School of China West Normal University, Nanchong Sichuan 637002, China)

In this paper, a new iterative algorithm is introduced in Hilbert space. A strong convergence theorem of equilibrium problems variation inequalities problem and a Family of countablek-Strict Pseudo-contraction Mapping is obtained. The result presented improves and extends the recent corresponding announced by many others.

2012-10-24

教育部科学技术重点项目(211163)

冯仁勇(1983—)，男，四川广元人.硕士研究生，主要从事非线性分析研究；

何中全(1955—)，男，四川南充人.教授，主要从事非线性分析研究.

0177.91

A

1674-5248(2013)02-0014-03