轮换对称性在多元微分学中的应用

湛华平，张书霞，陈鸿昊

（1.安阳工学院数理学院，河南 安阳455000；2.安阳一中，河南 安阳455000）

对称是指物体或图形在某种变换条件下，其相同部分出现有规律重复的现象，即在一定变换条件下的不变现象。亦指数学概念、公式、命题结构的形式具有对称性。在几何上，圆、抛物线、椭圆等都具有对称性，对称的概念在数学领域及其它很多方面一直起着重要的作用。在处理高等数学的许多问题时，对称性的利用是极为有效的，并由此得到问题简捷的解答途径，巧妙地应用对称性对于学好高等数学是十分重要的。

多元微积分的计算是高等数学的重点，也是难点。在计算过程中，很多问题如果运用一般的求解方法，会使问题变得复杂化，增加了计算量。而如果利用对称性和函数的奇偶性往往能使计算简捷[1－4]，达到事半功倍的效果。轮换对称性作为对称性中的一种，在某些积分的运算中，若积分区域具有轮换对称性，则可以简化积分的运算过程，提高运算效率。轮换对称性目前主要应用于二重积分、三重积分、曲线积分和曲面积分的简化运算。然而在多元函数的极限、偏导数、全微分、隐函数求导和求条件极值方面的应用却比较薄弱，类似的文献[5－7]和著作也很少。本文主要给出了轮换对称性应用于多元函数求偏导的命题和应用例子，及指导多元函数条件极值的简化方法。

1 轮换对称性

定义1 设函数F（x1，x2，…xn）＝F（x2，x3，…xn，x1）＝ …F（xn，x1，…xn－1），则称函数F（x1，x2，…xn）关于x1，x2，…，xn具有轮换对称性。

如果有f（x，y）＝f（y，x）成立，则二元函数f（x，y）关于x，y具有轮换性；如果有f（x，y，z）＝f（y，x，z）成立，则f（x，y，z）关于三元函数x，y具有轮换对称性。例如f（x，y）＝ （xy）x＋y和u＝ex2＋y2＋z分别具有关于x，y的轮换对称性。

2 轮换对称性在求偏导数中的应用

多元函数的偏导数、全微分、复合函数求偏导、隐函数求偏导等内容实则主要是关于偏导数的计算，可以按照高等数学教材给出的方法计算得到结果，但计算量偏大，下面给出可以简化偏导数计算的结果。

命题 如果二元函数f（x，y）的偏导数存在，又有f（x，y）＝f（y，x），则当时，有＝g（y，x）。

证 由偏导数的定义及条件得

由极限和无穷小的关系得

当 （u，ν）取 （y，x）时，可得

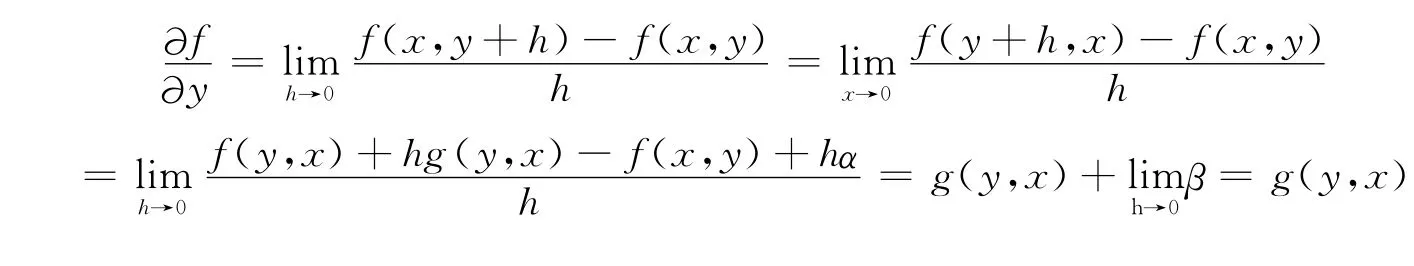
证毕。

接着来看该命题在简化计算中的妙用。

解 函数f（x，y）在（0，0）处对x的偏导数为

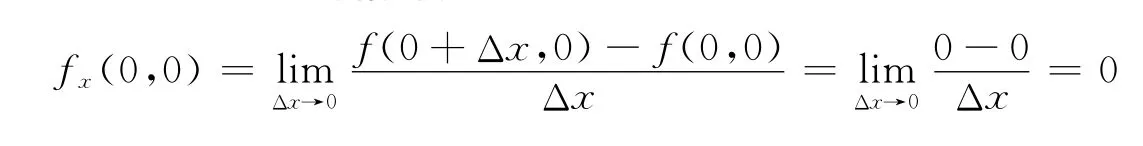
由轮换对称性可得

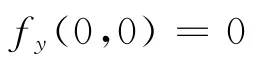
例2 设u＝f（x＋y＋z，x2＋y2＋z2），求

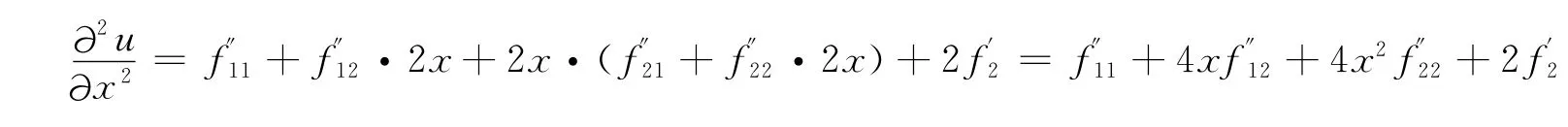
因为函数u关于x，y，z具有轮换对称性，所以

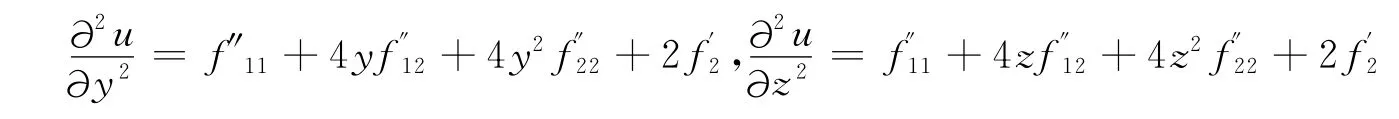
解 在计算fx（0，0，0）的过程中，变量y和z一直是看作常数的，故在求解fx（x，y，z）时，把y＝0和z＝0代入其中，可以得到

显然，函数f（x，y，z）关于x、y和z具有轮换对称性，因此

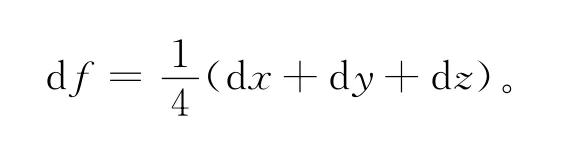
3 轮换对称性在求条件极值中的应用

在实际问题中，通常会遇到函数的自变量有附加条件的极值问题。对自变量有附加条件的极值称为条件极值。对于某些实际问题，可以将条件极值转化为无条件极值来求解。但在很多情况下，将条件极值转化为无条件极值很复杂。而拉格朗日数乘法可以直接求解条件极值。但是在转化的过程中拉格朗日函数的自变量将增多，这种由两元增加为四元、四元增加为六元的情况看似复杂，在实际计算过程中可以从问题本身出发，应用轮换对称性，直接得到变量之间的一些关系，从而很容易解出结果。

不加证明地给出如下结果：当f（x，y），φ（x，y）连续可微、且具有轮换对称性时，若求f（x，y）在条件φ（x，y）＝0下的条件极值，则用拉格朗日数乘法构造出的拉格朗日函数在计算驻点的过程中有x＝y。一般地，由拉格朗日数乘法确定的只是可能的极值点，如何确定所求的是否是极值点，在实际问题中需要根据问题的性质来确定。该思想方法可推广到更多变量和多个条件的情形。

例4 求函数u＝xyz在附加条件

下的极值。

解 构造拉格朗日函数

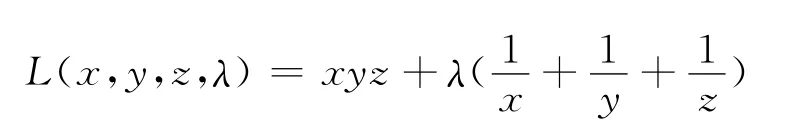
分别对x，y，z求偏导数并使之等于0，将其与附加条件联立得方程组

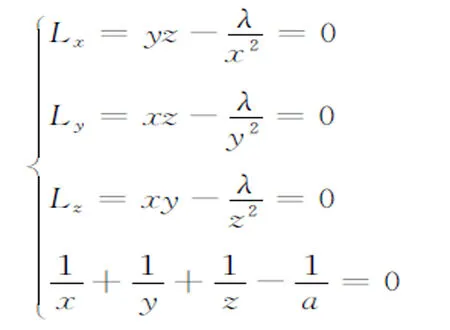
因为函数L（x，y，z，λ）关于x，y，z具有轮换对称性，所以有x＝y＝z，将其代入条件得x＝y＝z＝3a。由此得到点（3a，3a，3a）是函数u＝xyz在条件下唯一可能的极值点。应用二元函数的充分条件判断可知，点（3a，3a，3a）是该函数在其附加条件下的极小值。

如果所给的函数具有轮换对称性，则在计算偏导和条件极值的过程中可以简化计算。在解题过程中要结合所学的知识，善于发现问题隐含的信息，不要受定向思维的束缚，大胆创新，这对于提高解题和运算能力都有着非常实际的意义。

[1]徐年方.轮换对称性在积分计算中的应用[J].河北能源职业技术学院学报，2009，（01）：92－93；96.

[2]陈云新.轮换对称性在积分中的应用[J].高等数学研究，2001，（01）：28－30.

[3]于信，李秀珍.对称性在多元函数积分中的应用[J].山东商业职业技术学院学报，2004，（12）：75－77.

[4]景慧丽，赵伟舟，杨宝珍，等.第二类平面曲线曲线积分的计算探讨[J].甘肃联合大学学报：自然科学版，2012，26（06）：99－102.

[5]薛文娟.轮换对称性在积分中的应用[J].考试周刊，2001，（58）：45－46.

[6]朱莉.微积分中轮换对称性的应用[J].科技信息，2010，（24）：105.

[7]李凤萍.轮换对称性在高等数学中的应用举例[J].教育论坛，2012，（11）：156－157.