论大国交战函数*——基于“历史材料+科学方法”的研究范式

邓曦泽

一、历史现象提出的问题及其研究方法

笔者在分析春秋战争时，发现一类奇怪现象:大国争霸，但大国之间却很少直接交战。例如，晋楚拉锯争霸期间，两国只发生了7次战争，倒是两国与对方集团的其他国家进行了不少战争。这一重要历史现象提出了一个问题:既然晋楚都想争夺霸权，但为何要尽量避免交战呢?在此疑问下，再看20世纪后半叶的美苏争霸，则会发现更让人诧异的现象:美苏争霸期间，两国居然从未进行过正面战争。这难免让人疑问:大国之间没有正面战争的争霸，还算是争霸吗?进一步考察，则又发现:大国之间并非总是避战，有时也频繁征战。例如，战国时期大国的相互征战就非常密集;两次世界大战期间，大国之间的战争也非常密集。两类相反的历史现象都提出了一个一般性问题:大国之间交战的条件是什么?

本文没有事先预设问题，上述问题完全来自对历史材料的解读与分析。虽然本文与历史学有交集，但笔者并不打算沿用传统的历史学研究方法，而准备引入新的研究方法——科学研究方法。

人类最重要的活动是知识生产，任何个体只有先掌握一定的知识，才能用知识去生产，这意味着，越能生产有效知识的学科越重要。同时，人类生产知识的方式是多种多样的，如历史学、政治学、哲学、经济学、管理学、数学、逻辑学、物理学、化学，等等。但是，每种知识生产方式生产有效知识的能力并不相同。以历史学而论，古代的历史学具有强大的知识生产功能。历史学的主要方法有二:其一，大量记录事件，这些事件构成丰富样本;其二，运用归纳法，对样本进行归纳，发现一些规律。此两点较为接近现代科学方法。这意味着，历史学作为一种经验归纳的知识生产方式，具有进行有效理论建构的功能，并成为古代最重要的知识生产方式，而历史学也颇为繁荣。但是，自现代科学产生以来，它引入数理方法，在方法上形成“数学+实验”的基本模式，具有更强大的知识生产功能。自然科学的研究方法运用于社会领域，形成功能也十分强大的社会科学。社会科学使传统的历史学、哲学等学科相形见绌，这些传统学科也就日渐式微①［美］杜威:《确定性的寻求——关于知行关系的研究》，傅统先译，上海人民出版社2005年版，第20页。。

如何才能让历史学具有更强的知识生产功能?把历史 (或历史材料)放在问题之下，进行问题研究，同时引入科学方法 (如数理的方法)，是历史学重振知识生产功能的有效出路。

基于上述观点，本文试图在传统历史学方法 (样本+归纳)的基础上，引入科学方法，以“历史材料+科学方法”的范式来研究历史，更完整的表述则是“问题+历史材料+科学方法+一般结论”的研究范式。从历史中发现问题，运用历史材料和现代科学方法解决问题，并尽可能获得具有一般性规律的结论，从而比传统历史学更有效地生产有效知识 (关于本文的方法论，另有专文讨论②邓曦泽:《发现理论还是验证理论——现代科学视域下历史研究的困境及出路》，《学术月刊》2013年第4期;邓曦泽:《问题研究与文本研究——基于知识生产视角的学术方法论探讨》，《中国人民大学学报》2013年第5期。另外，笔者主张用科学方法解决问题，走科学化道路，但在实践上，笔者还处于尝试阶段。)。

二、大国争霸力避热战:以晋楚争霸与美苏争霸为例

笔者曾对《左传》所记载的战争进行了完全统计，形成了《春秋左传战争表》③邓勇 (邓曦泽):《王霸:正义与秩序——从春秋战争到普遍正义》之附录2《春秋左传战争表》，武汉大学博士论文，2007年，第270—295页。以下引《春秋左传战争表》，均来自此博士论文。。根据此表，可以具体把握春秋战争与天下秩序的互动。晋文公之后，天下进入晋楚拉锯争霸时期。晋楚拉锯的重要任务，是争夺宋国与郑国。因为宋、郑二国地处中原腹地，地缘政治价值重大，为晋楚必争之地。根据《春秋左传战争表》，再统计宋、郑两国参与的战争，并对这些战争的敌友关系进行分类，可以把握晋楚拉锯大势，并可制作成晋楚拉锯情况表 (见表1)。

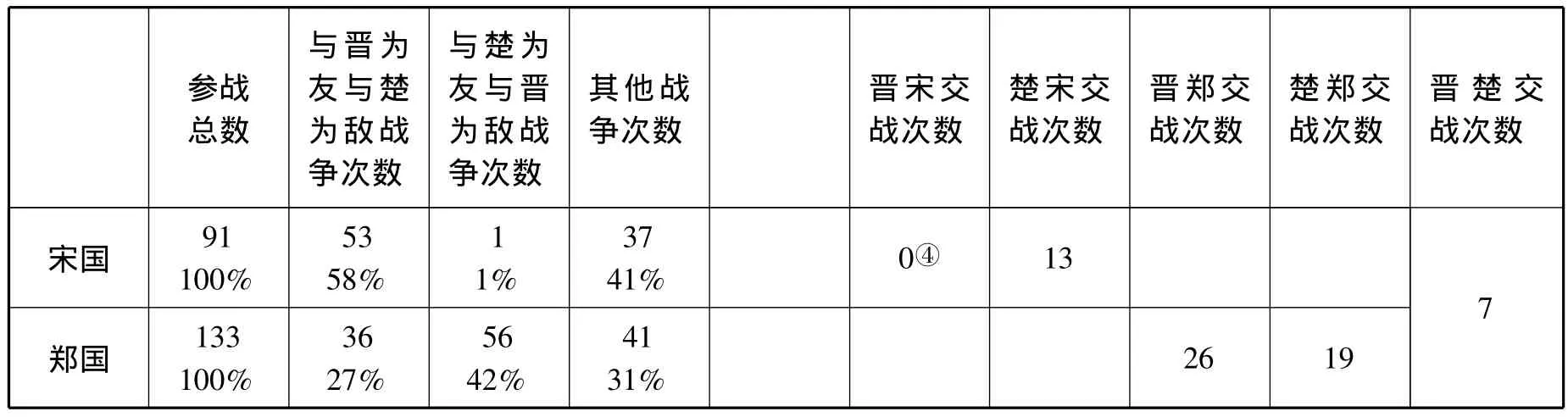
表1 晋楚拉锯情况表

晋楚拉锯期间 (公元前627年—前546年，即始于晋襄公即位，终于弥兵大会，凡80年)，两国直接交战仅7次:(1)公元前624年，晋伐楚救江;(2)同年，周晋伐楚;(3)公元前597年，晋楚邲之战;(4)公元前583年，晋侵楚;(5)公元前575年，晋楚鄢陵之战;(6)公元前572年，晋等侵楚陈;(7)公元前557年，晋师伐楚①这7次战争在《春秋左传战争表》中的编号是248、249、342、386、409、429、490。。其中，只有第3、5次是大规模战争。但是，楚国与宋国的正面战争达13次，与郑国的正面战争达19次;晋国与郑国的正面战争达26次。如果加上晋国或楚国指使其他诸侯国与宋国、郑国进行的战争，即加上晋与郑、楚与宋、楚与郑之间的间接战争，则宋国与楚国为敌的战争为53次，占宋国参战总数的58%;郑国与楚国为敌的战争为36次，占郑国参战总数的27%;郑国与晋国为敌的战争为56次，占郑国参战总数的42%。除此以外，晋国、楚国还与其他诸侯国进行了不少战争。

此外，晋楚拉锯之前，齐桓公时期，齐楚没有任何正面交战，召陵之盟是双方不战而退。晋文公时期，晋楚只有一次正面战争，即城濮之战。

上述统计数据让人产生疑问:既然是晋楚争霸，为什么晋楚之间不进行大量正面战争，击垮对方，反而与其他诸侯国进行了不少战争呢?通过下文的考察，笔者发现，在两极多边格局下，争霸双方会尽可能避免热战 (Hot War)，因为双方要避免相互削弱而使其他方进入争霸格局。于是，双方主要采取冷战 (Cold War)形式。

晋文公之后到春秋末期，春秋政局再也没有产生齐桓、晋文这样的全局性霸主。在当时的天下体系 (周朝体系)中，晋楚要争夺的不是地区性霸主 (即局部性霸主)，而是天下霸主 (即全局性霸主)。在当时，具有争夺天下霸主潜力的并非只有晋、楚，还有齐、秦。根据争霸的实力与潜力，可以这样看待当时的争霸局势:晋、楚、齐、秦都已是地区性霸主，但晋、楚实力最强，是第一梯队的争霸者;齐、秦实力次之，是第二梯队的争霸者。晋文公之后，春秋争霸格局可概括为两极两边:两极是晋、楚;两边是齐、秦。后来的吴、越，只是昙花一现，未构成稳定的一边。根据两极两边格局，如果晋、楚经常直接交战 (尤其是经常进行城濮之战、邲之战这样的大规模战争)，一方的确可能击垮另一方;但是，胜者也会付出巨大代价，实力会被严重削弱。如果晋、楚的实力被削弱到与齐、秦相当，甚至弱于齐、秦，则“鹬蚌相争，渔翁得利”，齐、秦一定会趁势而起，争夺天下霸主。那么，争夺天下霸主的国家就增加到四个，这对于晋、楚都不是好事。所以，一方面，晋、楚在争霸问题上绝不妥协、退让;另一方面，双方尽可能避免直接交战而两败俱伤。

在尽可能避免热战的情况下，晋楚如何争霸呢?双方采取的战略都是争夺势力范围、加强军备等冷战方式。例如，晋国从公元前678年拥有一军，然后扩充到二军 (公元前661年)，再到三军 (公元前633年)，再到五军 (公元前629年)，只花了不到50年时间 (见《左传》庄公十六年、闵公元年、僖公二十七年、僖公三十一年)，后又僭越周王，作了六军，与周天子相匹敌(公元前588年，见《左传·成公三年》)。扩张势力范围主要表现为大国通过软硬兼施的手段，使尽可能多的诸侯国进入自己的阵营，甚至成为盟国。扩张势力范围在争霸中具有战略意义，因为势力范围扩张，就意味着拥有更多可利用的土地、人口、兵源、粮食等重要战略资源，从而逐渐增加自己的实力，扩大与对方的实力差距而间接削弱对方。而势力范围的大小，表现为控制诸侯国的多少。其他诸侯国的实力与晋楚相比，显然很不对称;是故，晋或楚征服其他诸侯国远比晋、楚征服对方更容易，风险更小，所以，晋楚都竭力控制其他诸侯国。对于势力范围，又有重要地区与非重要地区的差别。在当时地缘政治中，“中州为天下之枢，而宋、郑为大国，地居要害，国又差强。故伯之未兴也，宋与郑常相斗争。逮伯之兴，宋、郑常供车赋，洁玉帛牺牲以待于境上，亦地势然也”②顾栋高:《春秋大事表》，中华书局1993年版，第1843页。。宋、郑两国，因其具有重要的政治、军事价值，而成为晋、楚两个争霸者都志在必得的诸侯国。于是，宋、郑两国经历的战争也特别多①宋杰:《春秋战争之地域分析与列国的争霸方略 (下)》，《首都师范大学学报》1999年3期。。晋、楚还以争夺宋、郑两国为枢纽，争夺其他诸侯国。当争夺势力范围成为争霸的主要途径后，晋楚两国的主要交战对象就转换为其他诸侯国。于是，经常发生如下情况:晋国争取了郑国，楚国就会攻打郑国;晋国担心丢失郑国，就会来救郑国;而晋国来救郑国时，楚国就会跑。或者:楚国争取了郑国，晋国就会攻打郑国;楚国赶过来救郑国，晋国也会跑。这就是晋楚拉锯的典型表现。晋或楚与对方集团其他诸侯国交战，试图将之纳入自己的势力范围，这属于热战，只不过是大国与小国的热战;晋与楚却相互避其锋芒，而不直接交战，这就是冷战。这种拉锯将热战与冷战相结合，成为最重要的争霸手段。并且，晋和楚还指使小国为之进行代理战争 (proxy war，或译“代理人战争”)。例如，公元前607年春，“郑公子归生受命于楚，伐宋。宋华元、乐吕御之。二月壬子，战于大棘，宋师败绩”(《左传·宣公二年》);又如，公元前585年秋，“孟献子、叔孙宣伯侵宋，晋命也”(《左传·成公六年》)②邓曦泽:《论春秋时期的代理战争》，《云南大学学报》2011年第6期;《中国社会科学文摘》2012年第3期全文转载。《左传》一共记载了12次代理战争。这12次代理战争在《春秋左传战争表》中的编号为25、112、298、374、394、432、440、463、512、611、626、640。。这些现象又说明了什么呢?同样，晋楚双方都不愿意硬碰硬而两败俱伤，所以希望牺牲小国的利益来保存或壮大自己的实力。

若将春秋争霸格局与20世纪后半期国际政治中的争霸格局相比较，则更能明白晋楚为何尽力避免直接交战。20世纪后半期，世界格局可概括为两极多边:两极为美国与苏联，多边为中国、印度等。此期国际政治的基本格局是美苏争霸。但诡异的是，第二次世界大战后，美苏之间从来没有进行过热战，甚至小规模的擦枪走火都没有，而只是冷战，即通过争夺势力范围、代理战争、科技和军备竞赛、外交竞争等非直接交战方式进行冷战，相互遏制却又不诉诸武力。争夺势力范围的最主要表现，就是北约与华约的形成，两大集团相互对抗。晋楚拉锯与美苏争霸对势力范围的争夺，同出一辙。在这个意义上，历史在不断重演。

朝鲜战争期间，苏联对中国予以了军事支持，帮助中国抗击美国 (包括暗中排遣军事人员参与中国人民志愿军，与美国为首的联军作战)。美苏都针对对方进行了大量间谍战、策反活动，美苏之间经常进行措辞强烈的外交对抗，火药味十足的武力威慑，不但出现了古巴导弹危机这样的事件，还出现了星球大战计划这样的军备竞赛，但是，美苏从来没有直接交锋。美国倒是在朝鲜战争、越南战争中与中国、朝鲜、越南等国家进行过战争，在伊朗政变、危地马拉政变、刚果内战中武装干涉他国，在历次中东战争中支持以色列。苏联则曾入侵捷克斯洛伐克、入侵阿富汗，并入侵珍宝岛而与中国进行了珍宝岛战役。美苏都竭力争取自己的势力范围。例如，美国介入伊朗政变就是要控制伊朗，支持以色列是为了制约阿拉伯国家，并进一步控制具有石油战略资源的中东。苏联入侵阿富汗，则是因为阿富汗在西亚具有重要地缘政治价值。美苏尽量避免直接交锋，绝不是基于道德考量，而是基于利益考量。如果美苏直接交战，胜者也会元气大伤，其他国家则很可能趁势而起。于是，美苏不但力避“热战”而相互削弱，还阻隔他国争夺世界霸权。例如，1963年，苏、美、英三国在莫斯科签署的《关于禁止在大气层、外层空间和水下进行核武器爆炸实验的条约》，乃是因为他们已进行了充分的水下、大气层的核试验，并将核试验转入地下。于是，他们禁止其他国家进行同类试验，其目的在于巩固核垄断地位，从而使霸权保留在美苏之间分配，而不至于分散。

但是，大国之间并非总是避战。如果大国之间的实力对比发生重大变化，则大国比较容易发生热战。例如，战国时期和两次世界大战期间，大国之间的战争就非常密集。

两类相反的历史现象提出了一个一般性问题:大国在何种条件下可能交战?

三、大国交战函数及其解释力

根据以上案例，可以归纳出大国交战的规律:在两极多边格局中，争霸的大国会尽可能避免正面交战，以免相互削弱而让其他方参与争霸;但是，在其他格局中，大国之间却较容易正面交战。为了严格、准确地考察大国争霸正面交战的条件与可能性，可以建立大国交战可能性函数。在几种格局中，两极多边可以视作一般模型，因为若多边取值为0，则多边不复存在，即为对决格局，所以，这里从两极多边格局切入。两极多边的博弈格局，可以图示如下:

(1)设:在一定时段内，两极的弱极与强极之实力比为F。两极也就是第一梯队的争霸者。

若此，1－F就是两极的实力悬殊。

(2)再设:多边所构成的挑战两极的实力与两极中弱极的实力比为G。

若此，1－G就是多边与两极的实力悬殊。多边对两极的挑战，包括单边对两极的挑战和多边联合起来对两极的挑战 (见图1“两极多边博弈结构图”)。

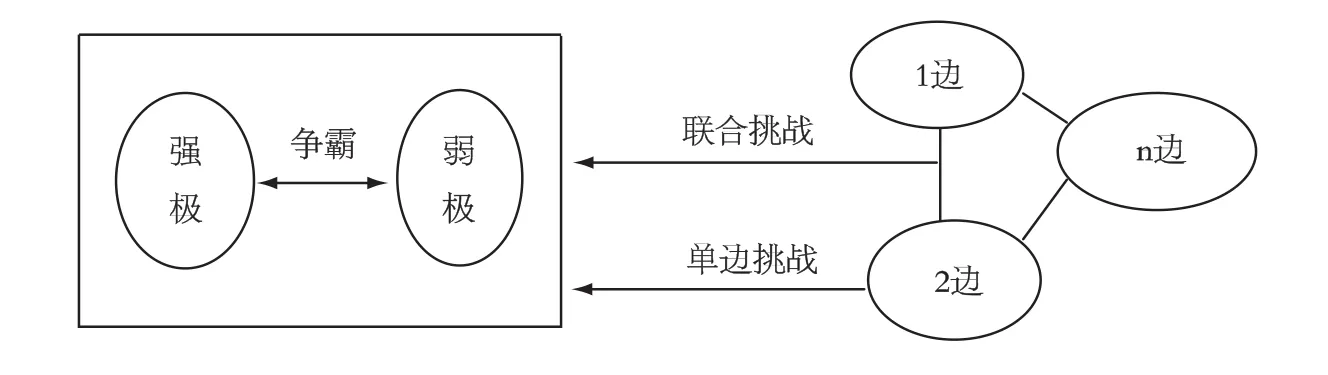
图1 两极多边博弈结构图

(3)再设:两极直接交战的可能性为P。

(4)若此，P=(1－F)(1－G)。(0≤F≤1，0≤G≤1)

此函数就是大国交战可能性函数，简称为“大国交战函数”。这个函数的含义是:两极实力的悬殊程度与两极直接交战的可能性成正相关关系;同时，多边与两极的实力悬殊程度与两极直接交战的可能性也成正相关关系。这个含义也就是大国争霸正面交战可能性规律的自然语言表述。

为什么 (1－F)与 (1－G)之间是乘积关系呢?因为二者相互独立，从两极之间实力悬殊情况推不出多边与两极之间的实力悬殊情况，反之亦然。

大国交战函数的数学形式一点也不复杂，但它能反映大国之间 (尤其是两极之间)的实力对比变化以及基于这种变化的相互博弈和该变化与大国交战可能性的关系。国家之间是否发生战争，取决于实力对比。F与G两个实力比值可以反映国家之间实力对比情况。并且，此函数区分了两极 (大国)的实力对比，多边 (次大国)与两极的实力对比，这两种对比 (即两个基本参数)足以影响国际秩序的变动。

具体言之，大国交战函数的功能表现为:

第一，大国交战函数可有效反映两极多边争霸的制衡格局。

在理论上，F、G的取值本可以是任意的，但实际上，只有在一定的取值范围内，体系才表现为两极多边的制衡博弈。F的值不能过小，即两极实力不能过于悬殊，否则，弱极就没有实力与强极争霸。这里倾向于将F的值取为0.5至1之间，将两极的实力悬殊控制在一倍之内。如果F的值小于0.5，则两极争霸格局很容易被打破，而呈现为吞并格局 (参见下文)。同理，这里倾向于将G的取值范围也限定在0.5至1之间，因为当实力悬殊超过一倍时，多边无法挤入两极，参与争夺全局性霸主。

1－F越小，两极实力越趋于平衡，则热战对双方的损害越大。此时，如果G越大，即多边的实力越强，则多边中的某些边就越有可能借助两极相互削弱之机而进入第一梯队，导致三者甚至更多者来争夺体系主导权，这对两极显然不利。因此，两极会尽可能避免热战而相互削弱，这表现为，P的值很小。但是，不能从P的值很小就推出两极一定不会热战的结论。这种可能性论证不是必然性论证，只要某个事件发生的可能性大于0，该事件就有可能发生。美苏在事实上从来没有热战，不等于美苏在逻辑上不可能热战。

这第一种情况，其实就是结构现实主义的数学表达。这种表达主要反映的是单元 (两极与多边)之间的实力分配与制衡，而不涉及单元的特性，也就是“不关心各个国家具有什么样的传统、习惯、目标、愿望和政府形式”①［美］肯尼思·华尔兹:《国际政治理论》，信强译，上海人民出版社2003年版，第131页。华尔兹在分析时所引入的市场理论，不但不会削弱反而会强化大国交战函数，大国之间的实力制衡与市场博弈的确有相类之处。在某种意义上，两极就是争夺垄断地位的大公司，多边就是第二梯队的公司，两个大公司为了避免两败俱伤，也会尽量避免直接攻击对方(《国际政治理论》，第120—122页)。。其实，华尔兹 (Kenneth N.Waltz)的结构现实主义对体系结构的表述并不清楚。根据大国交战函数，只要给出两极实力的悬殊程度、多边与两极的实力悬殊程度这两个参数，再将两个参数的取值限定在一定范围 (0.5至1之间)，就可以比较清楚地反映制衡结构的基本特征。但是，这种制衡格局未必稳定。要保持制衡的均势，需要很多条件，需要各个单元同步、协调的变化。如果某个单元的内政出了问题，导致实力削弱，该单元的变化就会引起体系秩序的大变动。例如，苏联的解体结束了美苏争霸的基本格局，改变了世界秩序。当制衡格局被改变后，就会演变出吞并格局或更替格局。

据大国交战函数，我们还可以理解结构现实主义的历史背景，理解它为何在20世纪70—80年代风行。20世纪70年代，正是冷战高峰期，当时大国的实力对比，比较符合这里的F、G的取值。美苏既对抗又不首先攻击对方，这是一种典型的制衡结构。所以，结构现实主义的代表作《国际政治理论》在1970年代末出版，不是偶然的。

第二，大国交战函数可推演出吞并格局。

当F、G处于一定取值范围内时，大国交战函数就呈现为吞并格局。吞并格局又分为两种情况。(1)F小于0.5，1－F越大，两极实力悬殊越大，则两极争霸格局不复存在;同时，G也小于0.5，则多边不复存在。若此，原来两极的强极，就开始吞并其他各方，体系就呈现为大国吞并小国的格局。这表现为，P的值较大。例如，战国后期，秦国吞并六国，就是吞并格局。(2)F趋近于1，则两极实力相当;同时，G很小 (小于0.5)，则多边不复存在。若此，体系呈现为两极对决格局。典型的案例是项羽与刘邦的楚汉争霸②华尔兹说，20世纪20—40年代，中国在名义上是一个国家，但整体上处于无政府状态，故更像彼此分离共存的国家(《国际政治理论》，第153页)。楚汉之争时期的中国也属于这种情况，当时的天下处于无政府状态，楚汉要争夺的，就是天下主导权，故这里以楚汉争霸为例，是合理的。。此时，并不存在多边，只有两极。在这种情况下，自认为可以战胜对方的那一方，就很可能发动战争，攻击对方。因为它知道，它不必担心自己胜利之后却被第三方威胁，只要自己胜利了，即便付出沉重代价，它也能垄断天下主导权。在楚汉相争中，先是项羽认为可以战胜刘邦，后是刘邦认为可以战胜项羽，这就大大增加了热战的可能性。根据大国交战函数，则很容易理解楚汉为什么要对决。

大国交战函数对吞并格局的描述，其实就是对进攻性现实主义的描述，只不过这里采用了“吞并”这一措辞。米尔斯海默 (John J.Mearsheimer)认为，“每个国家压倒一切的目标是最大化地占有世界权力，这就意味着一国获取权力是以牺牲他国为代价的。然而，大国不止是为了争当大国中的强中之强，尽管这是受欢迎的结果;它们的最终目标是成为霸主 (hegemon)，即体系中唯一的大国”③［美］约翰·米尔斯海默:《大国政治的悲剧》，王义桅、唐小松译，上海人民出版社2008年版，第2页。。当某大国的实力超过其他国家而达到一定程度，大国就很可能发动热战，彻底征服其他国家，获得体系主导权。就地区性体系看，这种吞并格局在战国末期出现过;而就全球性体系看，至今尚未出现吞并格局，因为至今没有任何国家具有吞并全球其他国家的实力。同样，运用大国交战函数，也能更清楚地解释进攻性现实主义结构。

根据大国交战函数，也可以更好地理解《大国政治的悲剧》的时代背景。20世纪末，世界并没有表现出冷战结束后有些人所期望的和平，大国的冲突未必不可能。米尔斯海默在2001年出版的《大国政治的悲剧》，可以说是对20世纪最后阶段国际秩序的描述与对未来的预测。在某种意义上，历史部分印证了米尔斯海默的看法，1991年至今的20年间，美国就经历了科索沃战争、阿富汗战争、伊拉克战争;因美元增发而构成对国际社会的剥削，国际社会对美国的不满在增加;美俄在中东的角力，美中俄在朝鲜的角力，一直在进行;军备竞赛从未停止。只不过，米尔斯海默对大国冲突秩序作了放大和强化，将之上升为大国博弈的一般模式。但实际上，《大国政治的悲剧》所揭示的只是大国博弈的一种模式。该模式在某些时期可能比较凸显，在某些时期则会大为消退。

第三，大国交战函数可描述争霸者的更替格局。

当F小于0.5，则两极实力悬殊较大，则较容易发生热战。同时，如果G越大，接近两极中的弱极，则多边也更可能挑战两极中的弱极，使多边中的强极跻身于两极。这表现为，1－F较大，而1－G较小，P的值既不是很小也不是很大。例如，1588年，英国在与西班牙无敌舰队的海战中大获全胜，从而成为霸主;第一次世界大战前，美国并不够强大，但通过一战、二战，欧洲传统大国相互损伤而元气大伤，美国、苏联则成为超级大国。

第四，大国交战函数可描述多边脆弱制衡格局及其转向混战格局。

如果不存在大国，只存在多个实力相当的国家，则多国之间只能是脆弱的制衡，并转向混战格局。因为同等实力的国家越多，这些国家就越难达成共同认可的规则和契约，也就是说，交易成本更高。而只要一国破坏制衡，多边制衡就很容易解体。用经济学的话讲，多边达成一致所需要的交易成本更高，因此更难达成一致;同时，若一边违反规则，打破制衡的概率为x，则同等实力的国家越多，制衡格局被打破的总概率会越高。这与多人合作做生意时违反协议的总概率越高是同样的道理。一旦制衡被打破，一次战争的胜负就可能改变各边的实力对比，胜者可能成为弱国、强国或不变，但输家肯定成为弱国。于是，体系很容易走向混战格局。此点可以解释中世纪欧洲为何多战。中国的战国初中期也是这种格局，初中期的混战，使实力逐步悬殊，到了战国晚期，秦国独大，从而为秦国吞并各国创造了条件。

上述第一点是本文所主要讨论的情况，第二、三、四点，则是大国交战函数兼具的功能。以上几点意味着，结构现实主义与进攻性现实主义都可以在大国交战函数中得到描述。同时，根据大国交战函数，可以发现这两种理论的不足。这两种理论都只能反映大国实力对比的一种情况，而不能反映更全面的情况;大国交战函数则可以全面反映大国在何种实力对比条件下选择或放弃战争手段，以及由此导致的体系格局的变化。

根据大国交战函数，再看看晋楚争霸。由于晋、楚两极实力相差不大，即1－F较小;同时，齐、秦两边实力也不弱，具有争夺天下霸主的潜力，即1－G较小;所以，晋、楚两国或者尽力避免正面交战以降低自己被淘汰出两极的可能，或者减少齐、楚争夺天下霸主的可能，这表现为P值较小，即两极交战可能性较小。

但是，不可因为晋、楚交战的可能性较小，就得出晋、楚之间有和平相处的可能。对于霸权争夺，两国毫不相让。在晋、楚拉锯时期，两国采取的争霸方式主要是冷战。他们努力争夺势力范围，扩充军备，为最终的大国对决作准备。晋、楚期望的是，齐、秦等多边削弱而不足为虑之后，就可以进行对决了，此种状况如楚、汉相争。在这个意义上，冷战是一种结构性现象，古已有之。冷战是两极多边争霸格局中两极争霸的常规形式，并且冷战格局可以从大国交战函数中推演出来。当1－F越小，且1－G越小 (F、G都大于0.5)，就是冷战。冷战格局也就是上述第一种情形。同样，美苏冷战期间，双方也主要致力于争夺势力范围，扩充军备。晋楚冷战与美苏冷战的区别在于，由于武器在现代战争制胜因素中所占的权重越来越大，因此，在现代冷战中，军备竞赛越来越受重视，越演越烈。各大国都只有努力扩充军备，才能维护自己的生存安全，并提高夺得世界霸权的可能性。

同时，也不可因为两极多边格局中两极热战的可能性较小，就得出两极不可能交战的结论。上述第二点之 (2)就说明了，在有多边的情况下，两极之所以尽可能避战，乃是积蓄力量，最终对决，争取胜利而获得体系主导权。当多边不复存在或不足为虑时，两极热战的可能性越来越大，并且很可能是大规模的全面战争。晋楚冷战、美苏冷战，所希望的是最终对决以主宰天下霸权。但是，时势的发展未必如晋、楚所愿。一方面，吴、越一度兴盛，使多边的实力更加强大，楚国被严重牵制;另一方面，春秋结束时，晋国一分为三，一极分解为三边，开启战国时代。两方面相结合，历史没有给晋、楚对决提供机会。同样，历史也没有给美、苏对决提供机会。由于苏联自身发展不好，导致苏联解体，而俄罗斯不足以与美国争霸，同时中国、印度等逐渐强大，因此，美、俄对决的可能性迅速降低。当然，这并不意味着对决是不可能的。如前所言，项羽与刘邦之间的对决，就相当于大国对决。

综上所述，大国交战函数的描述功能很强。如果给出两极与多边在一定时期内的实力数值，则大国交战函数可以比较准确地描述和预测此后一段时期的体系变化趋势①据此，笔者预测，二三十年以内，当今世界不会发生大规模战争，即美、俄、中三方中的任何两方都不可能进行大规模战争。。大国之间究竟是战是和，乃是大国根据实力对比与战争的成本、收益估量来确定的，“政治学家、经济学家、博弈理论家以及多数理智的政治领导人，通常根据可能的或实际的结果来评估特定的冲突，也就是说权衡冲突的得失、风险和代价”②［美］詹姆斯·多尔蒂、小罗伯特·普法尔茨格拉夫等:《争论中的国际关系理论》，阎学通、陈寒溪等译，世界知识出版社2003年版，第283页。。

在运用上，如何计算各国的实力，是一个很复杂、琐碎的事情，需要大量的调查、统计，并且不可能做到精确。不过，虽然国家实力不可能精确统计和计量，但毕竟还是可以大致衡量的(例如克莱恩提供的计算方法③引自［美］康威·汉得森《国际关系:世纪之交的冲突与合作》，金帆译，海南出版社、三环出版社2004年版，第101—102页。)。

当然，大国交战函数也有不足。大国交战函数把多边视作一个整体，无法描述多边之间的博弈。例如，此函数把欧盟视作一边，并没有考虑欧盟本身作为一个联合体，其内部还有许多博弈。而对于一个主权国家如中国、美国、法国、日本而言，则不需要考虑这种内部博弈。

四、大国交战函数的比较优势

在应用时，必须对大国交战函数的几个参数赋值。但是，由于我们几乎不可能获得各国实力的准确数据，所以，即便有了大国交战函数，也不可能准确计算大国交战的可能性。于是，有人将此视作大国交战函数的缺点。其实，这种看法有两点不足。其一，一般地看，它混淆了公式对参数之间关系的描述和对参数的赋值问题。赋值不是公式的任务，能否对参数赋予准确的值以及如何对参数赋值，皆与公式本身无关。这与三角形面积公式S=1/2dh的功能一样，该公式只回答底、高与面积的数学关系，至于如何获取底边和高的长度，不是该公式的任务。大国交战函数是在提供国家实力数据的基础上，描述大国交战的可能性及其走势。所以，如何获取关于国家实力的数据，不是大国交战函数的任务，而初始数据是否准确，也无关大国交战函数的优劣。其二，我们应该从比较优势角度来理解大国交战函数以及一切理论、方法的价值。在给出国家实力数据的情况下 (不管数据是否准确)，有大国交战函数与没有大国交战函数相比，前者更能准确描述与预测大国交战的可能性，这就是大国交战函数的比较优势。

由于比较优势可以作为一种研究方法，所以下文对之予以申述。

比较优势④这里说的比较优势是一般性概念，而经济学上的比较优势只是比较优势的一种具体情况。，亦可以称为进步主义，它是判断一个理论 (或方法、政策、法律等)相对于另一个理论是否具有优势的一种方法。人类面对各种各样的问题，提出了各种各样的解决方法，显然，并非每种方法都具有同样的效用。同时，人类总是在追求更有效的方法来解决问题。而要选择更有效的方法，前提是能有效判断不同方法的效用。如何判断不同理论 (广而言之，任何方法、手段、政策、制度等)的效用，是一个很复杂的问题，没有一个普遍适用的通行方法，这里只强调两点。

第一，用程度区分法比用有效与无效的二分法来衡量理论的优劣，更有效。人们常用的有效与无效这对概念过于粗略，不足以区分和衡量理论的有效性，因为许多理论既非完全无效，也非完全有效，而是有一定效用。一个理论 (或方法)的有效性程度可以在0和100%之间 (0≤x≤100%)。用程度来衡量，更能明晰不同理论之间的优劣，明白一种理论对另一种理论的比较优势，并有助于推动理论的有限进步，避免完美主义倾向。

第二，没有任何理论是绝对正确的，一切理论的有效性都是相对的。在相对有效的观念下，许多理论的价值都可以比较。一种理论是否有价值，不在于还有一些问题是它不能解决的，而在于它对解决以前的理论所未能解决的问题有何推进，在于有了它之后和有它之前相比，人们获得了哪些有益的新东西。因此，对于一种新理论、新主张，我们应该持相对进步的态度。这就是评价一个理论的创新及其价值的进步主义而非完美主义的原则。如果a理论的有效性是30%，b理论的有效性是50%①生活中常见的例子是，针对同一病症的药物，有的临床有效率为30%，有的为70%。，则:a＜b，即b理论比a理论更优。利用0≤a＜b≤100%这个表达式，我们可以描述式地界定比较优势和完美主义:如果认为b理论相对于a理论是进步的，则属于比较优势 (即进步主义)的观点;如果认为b理论相对于100%仍有种种缺点，从而否定b理论相对于a理论的进步，则是完美主义的观点。比较优势 (即进步主义)是有益的判定理论优劣的方法，它有助于推进理论点点滴滴的进步;而完美主义是有害无益的判定理论优劣的方法，它无助于推动理论的进步。任何进步在完美主义那里都是漏洞百出，不值得肯定的。

下面，我们可以建立比较优势 (即进步主义)的基本模型。B比A优越，不需要B没有缺点，只需要B比A有优势，有进步。如果满足下面两种情况之一，则B对于A具有比较优势:

(1)如果B具有A的所有优点，并且具有A所不具有的优点，并且A、B的缺点相同，则B对于A具有比较优势 (见表2模型1)。(2)如果A具有B的所有缺点，并且具有B所不具有的缺点，并且A、B的优点相同，则B对于A具有比较优势 (见表2模型2)。模型2实际上是模型1的变形。对这两种模型，可列表来表示。

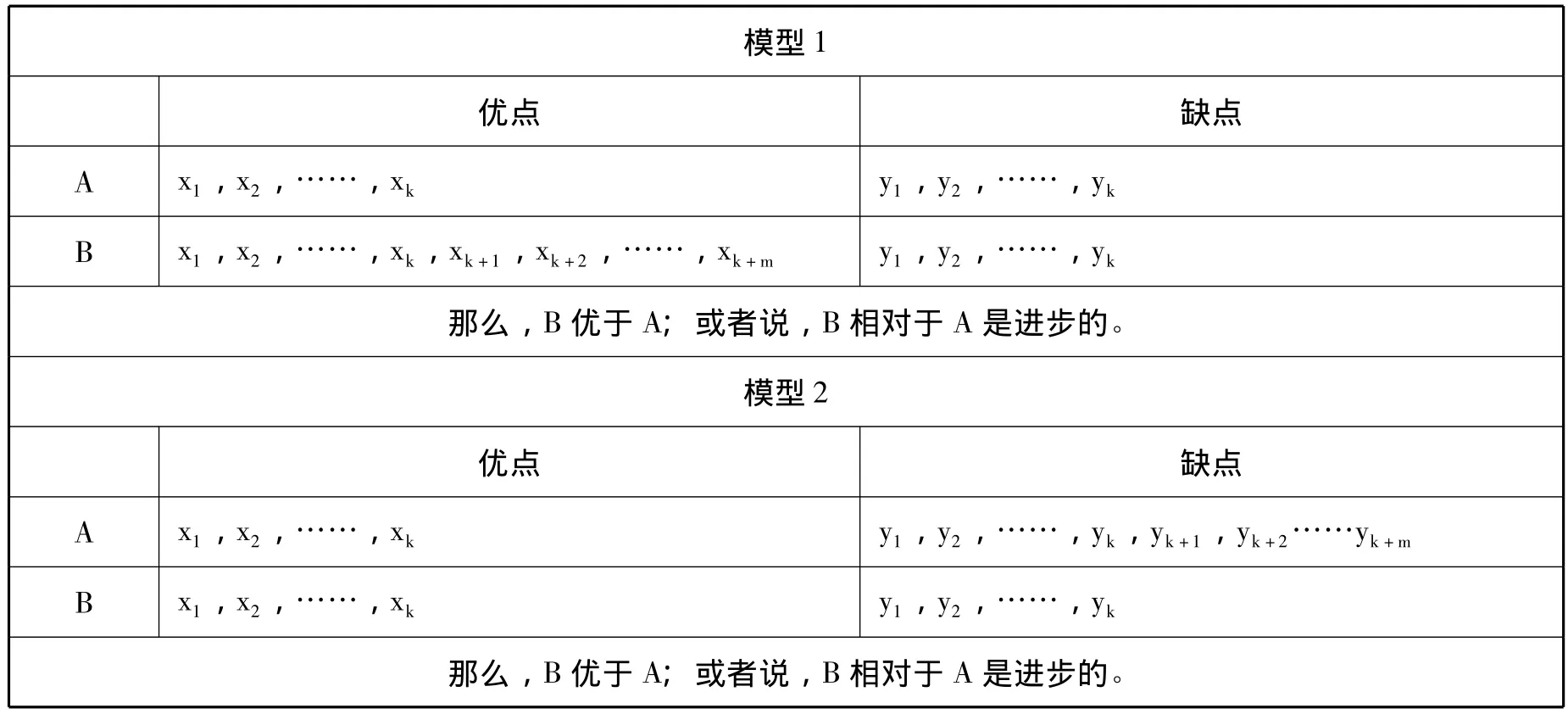
表2 比较优势 (进步主义)的模型

但是，上述模型并不适用于所有的理论比较，其适用前提是:(1)两个理论各自的优点、缺点都可以罗列出来，且得到争论各方的公认。如果两个理论各自具有什么优点、缺点都还在争论不休，就不满足运用上述模型的条件。(2)理论A与B的优点或缺点完全重叠。(3)不重叠的缺点或优点，一个必须完全包含另一个。

根据上述模型的适用前提，则可知其局限性:如果理论A与B的优点交叉 (不重叠，不包含)，或者二者的缺点交叉，则很难简单明了地判定谁优谁劣，而必须用更复杂的方法进行比较和判定。其实，比较优势模型的价值，本身也可以从比较优势角度来理解:如果两个理论满足比较优势模型的条件，则二者的优劣可以用比较优势模型来判定，这就是比较优势模型的比较优势。

上述关于比较优势/进步主义的模型，本不需要专门讨论，但很多人并没有明白此理，从而陷入完美主义的窠臼。完美主义的基本判定方式是:如果B还有一些缺点，则B是不好的。例如，完美主义者会说，因为B存在缺点y1，y2，……，yk，所以，B是不好的，这就是没有认识到比较优势。有些人虽然不承认自己是完美主义者，但由于对比较优势的基本判定模型缺乏自觉，也经常会不自觉地犯完美主义错误。

根据比较优势的模型，可以用列表的方式展现大国交战函数的比较优势 (见表3)。由于无论有无大国交战函数，调查统计任务都不是此函数的责任，故此点作为共有特点，不在表中体现。而关于大国实力的初始数据，可分三种情况。情况 (1):没有调查统计，只有模糊估值;情况 (2):有调查统计，但数据不够准确;情况 (3):有调查统计，且数据完全准确。通过对这三种情况的完全归纳，可以知道，无论哪种情况下，有大国交战函数比无大国交战函数都具有比较优势。

表3 大国交战函数的比较优势

例如，对于情况1，如果没有大国交战函数，人们面对模糊的估值，根本不知道如何考虑其间的关系。如果把两极中强极的实力估计为弱极的两倍以上，即F＜0.5，把余下多边与弱极的实力比G估计为大于0.5，那么，如果没有大国交战函数，人们根本不知道F、G之间是何种数学关系，也就不知道该用加法、减法还是其他什么方法来处理F、G与大国交战可能性的关系。但是，有了大国交战函数后，人们就知道P=(1－F)(1－G)，再将F、G的估值代入，则可以知道，P值较小，即大国交战可能性较小。这一估算是符合经验的，因为多边实力逼近弱极，如果强极直接攻打弱极，即便消灭了弱极，但由于自身实力的损伤，它也会再次面对多边的挑战。所以，强极稳妥的做法是避免与弱极热战。又如，对于情况3，即便给出了准确的数据，如果没有大国交战函数，人们面对这些数据，也不知道这些数据之间是什么数学关系，且不知道该用什么方法计算这些数据。而有了大国交战函数，则可以准确地计算。

综上所述，对大国交战函数的指责其实都是对有和无该函数这两种情况的共有缺点的指责，这种指责没有从比较优势来理解大国交战函数的价值，因而是不当的。