若干有向图的无穷小余代数的同调群的计算

李艳凤，刘海成，康文艳，王雪巍

（1.黑龙江八一农垦大学理学院，大庆163319；2.齐齐哈尔林业学校；3.齐齐哈尔市第一中学）

在20 世纪40 年代，人们受计算拓扑中的同调而发展起来的技巧和方法启发，定义和探索了一系列代数系统的同调与上同调[1]。Cartan 和Eilenberg[2]的专著对于同调理论作了系统的总结，他们运用模的投射与内射分解成功地定义了导出函子，完美地将各种同调理论统一起来。这是数学史上真正的变革，而且这是一个新的开始。

自从1945 年Malcane 与Eilenberg 提出范畴的概念和理论以来，它在数学的许多分支，例如代数几何学、拓扑学、微分几何学以及函数理论中均已有所应用。代数表示论主要研究有限维代数的结构[3-6]、不可分解表示和模范畴的构造。余代数是通过代数的对偶[7]定义的，在对代数的模范畴研究的基础上，余代数的余模范畴的研究对讨论余代数的结构与表示有重要意义。

①治疗后复查血液流变学各指标,评价脑循环改善情况,内容包括全血高切黏度、全血低切黏度、血浆黏度、纤维蛋白原、血细胞比容;血液黏度采用毛细管粘度测量法,纤维蛋白原采用ELISA法测定,血细胞比容采用离心法测定。②分别评估治疗前后神经功能及生活能力,采用NIHSS评分评价神经功能缺损程度,采用日常生活能力量表(ADL)评价生活能力改善情况;③记录各项细胞因子变化,包括TNF-α、IL-1、SOD、MDA、NT-proBNP,TNF-α、IL-1评价全身炎症状况,采用ELISA法测定;SOD、MDA评价体内自由基水平,采用比色法测定;NT-proBNP评价病情严重程度,采用荧光免疫分析法测定。

所以，根据代数复形的同调群理论来研究其对偶的余代数的同调群[8]。下面给出若干有向图的无穷小余代数的同调群的计算。

1 预备知识

设C 是一个有单位元1C的环，CM 为所有左C-模连同所有模同态所组成的模范畴。在CM 中取一系列C-模An，-∞＜n＜+∞，并取dn∈Hom（An，An-1），即得一列

如果对于所有的n，都有dndn+1=0，则称（A，d）为一个复形，或称为链。An为此复形的第n 次项，整数n为该项的次数，dn为其微分。如果所有微分都等于0，则此复形叫做平凡的。条件dndn+1=0 意味着Imdn+1⊆Kerdn，我们称商模Kerdn/Imdn+1=Hn（A，d）为复形 （A，d）的第n 个同调群。全体Hn（A，d）的集合{Hn（A，d）}叫做复形（A，d）的同调群H（A，d）。

定义1 设K 为一个域，C 为一个K 线性空间，△∈HomK（C，C⊗C）为一个线性映射，如果它们满足如下的条件：（I⊗Δ）Δ=（Δ⊗I）Δ，我们称（C，Δ）是一个K 余代数。

定义2 设Q是顶点集Q0和箭头（即有向边）集Q1均有限的有向图。对于任意非负整数n，用Qn表示以Q中长度为n的路径（简记为γ=a1a2Lan）全体的集合。设K为一个数域，记Qn为基的K向量空间为KQn。我们称向量空间kQ=⊕∞n=0kQn为图的道路向量空间。定义余乘法如下：

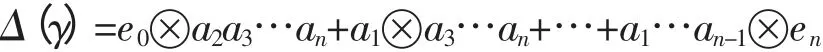
其中γ=a1a2Lan。不难验证，（KQ，Δ）为余代数。我们称这样得到的余代数为图Q的无穷小余代数，称KQi的非零元为（KQ，Δ）第i次成分。令，则（KQ[n]，Δ）为（KQ，Δ）的子余代数，我们称其为Q的n次无穷小余代数。

定义3 同调代数领域的基本对象是一个链复形（A*，d*）。这是一个由交换群、模或更广义地说是由一个阿贝尔范畴的对象组成的序列A0，A1，A2…。它们通过一系列同态dn:An→An-1相连，使得每两个连接的映射的合成为零：对所有n有dn◦dn+1=0

链复形的同调群定义为Hi（A*）=Ker（di）/Im（di+1）。

我们定义ei的次数为0，ai的次数为1，ai⊗aj的次数为2，…。由于

定义4 链复形概念的一个对偶版本是上链复形。一个上链复形（A*，d*）是个序列A0，A1，A2…。它们由一系列同态dn:An→An+1相连，使得任何两个接连的映射的合成为零：对所有n有dn+1◦dn=0

证明：我们用归纳法来证明：

2 无穷小余代数的Hochschild同调群

设Q是一没有分支的有向树，Q0是顶点的集合，Q1是长度为1的有向边的集合。我们有如下命题：

命题1 对于一个没有分支的有向路Q，设Q0={e0，e1，…，en}，Q1={a1，a2，…，an}，其中ai表示ei-1→ei的一个有向边。Q的余代数为C，则复形的H0≅K⊕K⊕…⊕K，其中K的个数为n+1，即该有向图的顶点的个数。

从行为方式上来看，负面清单模式是相较于政府主动管制行为的一种相对被动的管理方式，单纯依赖于负面清单显然只能助长政府的惰性和社会经济主体的逐利性，也只是一种缺乏互动参与的单方面行为方式。从理论上讲，政府与市场并非市场管理中的单选题,两者能否互动以及如何互动才是问题的关键。在市场与政府间进行选择并不关系到制度完善或者不完善的是非问题，而是通过何种途径将不完善变得更完善，降低缺陷的程度。比较理性的选择并不一定要在完善的市场机制或者完善的政府管制之间二选一,而是要在不完善的政府和不完善的市场之间构建有效的协调互动机制,在博弈中寻求政府与市场的契合点,以保证现代市场经济的规范运行。

根据图10所示的同机器移动工序邻域结构示意图，同机器移动工序可分为两种情况：①将工序u移至v之后，如图11所示；②将工序v移至u之前，如图12所示。同机器移动工序与JSP中的邻域结构相似，因此，可以扩展Balas[4]所提出的近似评价方法，应用于FJSP的同机器移动工序。

关于链复形的种种定义可以照搬至上链复形；实质上，我们仅须将原定义中的所有箭头反转。例如上链复形的上同调群定义为Hi（A*）=Ker（di）/Im（di-1）。

n=1时就是有向图Q，Q0={e0，e1}，Q1={a1}：ai表示e1→e2的有向边。C中元素有形式x=k1a1+k2e1+k3e3，ki∈K，K是一个域。如果d1（x）=0，则x=k1e1+k2e2，从而H0≅K⊕K。

假设顶点数不超过n的都成立，则顶点数为n+1时：

远远的，我看见了吴小红。吴小红一见我眼圈就红了。原来，在我住院这段时间，吴小哥病情出现了反复，天天吵着要回古家庄，说古大富是不是一个人跑回古家庄了。就在前几天，吴小哥情绪有所平静，说想吃煮玉米。吴小红听了很高兴，就去街上买玉米。等她回来，吴小哥的轮椅已经从楼梯上摔了下来。

图5和图6分别是采用不同方法对浓度为0.1 mmol/L和0.03 mmol/L的样品溶液检测到的信号进行去噪后的结果。对比分析图5和图6可知,采用空域相关方法去噪,去噪后波峰的峰高和波峰位置形状几乎没有变化,但是基线相对粗糙;采用普通阈值方法去噪,去噪后信号第1个波峰的峰高分别减少了约0.45 mV和0.35 mV,影响对检测结果的分析;相较于现有方法,本文方法能在保持峰形和峰高不变的情况下,有效滤除信号中的噪声,提高信噪比。因此本文方法能有效提高检测仪的性能。

俞敏杰是顾晓琳在学习上的竞争对手。两个人学习上谁也不服谁，第一名的成绩轮流坐庄。不过，顾晓琳现在糟糕的家庭状况让俞敏杰为她担心起来，如果这种状况持续下去，她的成绩肯定要下降，可是如果因为这个原因成全自己在班里第一名的地位，自己好像有点儿胜之不武。

γij表示长度为i的道路，如果x∈kerdi=kerΔ，由于只有Δ（γn）的次数为n-1，从而kn=0。由于

选取评价指标是进行雷电灾害风险区划的基础，是分析和研究事物风险的切入点。本研究结合长沙地区的雷电灾害的实际情况，采用以下4个指标来分析长沙地区的雷灾易损性，包括雷击密度、雷击灾害频度、经济易损模数以及生命易损模数［10］。其中前两项指标着重于雷电和雷电灾害发生频率、次数的评价，反映致灾因子的时空分布和承灾体的受损程度，后两项指标则侧重于人员和经济损失的评估，反映承灾体的受损强度［11］。

那天晚上女人喝醉了，和她相处了五年多的男友弃她出国了，还拐走了她十几万元钱的存款。尤其不能让她原谅和伤心的是男友的不辞而别，听说还带了个年轻的女孩出去。

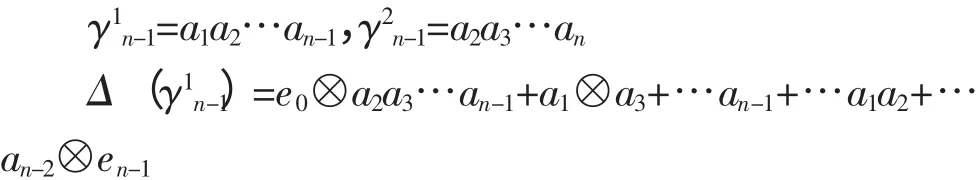
由于第一项中出现了e0，后面的每一项中都出现了a1。e0，a1在Δ（γ2n-1）的每一项中都不可能出现，而其余的γij次数又都＜n-2，因此k1n-1，k2n-1=0。类似的只要γ的长度不为0，其前面的系数全为0，因此x=k01e0+k01e1+…+k0n+1en。故H0≅K⊕K⊕…⊕K。即总共有n+1个K，其中n+1是该有向图的顶点的个数。证毕。

设Q是一有平行边的有向图，Q0是顶点的集合，Q1是长度为1的有向边的集合。我们有如下命题：

◎注意清洁保持干燥，拉完臭臭要洗屁屁、擦干，可以用电吹风吹，注意温度不能烫伤，最好选用带温控的电吹风。

从而△将任何一条路径降1次幂，这相当于一般代数中的微分算子。γ的次数为n，Δ（γ）的次数为n-1。我们可令

命题2 对于有向图Q，Q0={e0，e1}，Q1={a，b，c}，其中a，b是e1→e2的两条不同路径，C是e2→e1的一条路径，Q的余代数为C，则如下复形的H0，H1是平凡的：

证明：C2中的元素可以表示成x=k1ac+k2bc+k3ca+k4cb。我们可以计算出

则Δ（x）=（k1+k2）（e1⊗c）+k1（a⊗e0）+k2（b⊗e0）+（k3+k4）（c⊗e1）+k3（e1⊗a）+k4（e1⊗b）。

如果x∈kerΔ，可以解出k1=k2=k3=k4=0。即x=0，从而H0=0。

下面我们证明1阶同调群是平凡的。

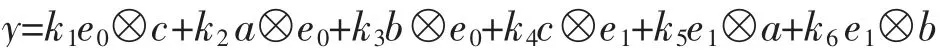
若y∈kerd2，则有

我们可以解出k1=k2+k3，k4=k5+k6，从而

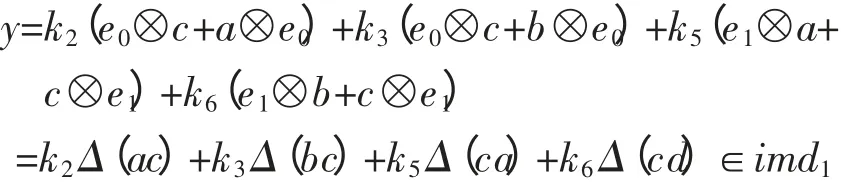
故H1=0。证毕。

3 结论

介绍了无穷小余代数、同调代数的基本概念。利用余代数可以看成其有限维子余代数的并，余模可以看成其有限维子余模的并，将所研究的无限维的情况转换成有限维来研究余代数的低阶同调群的计算。得出了有向图的无穷小余代数的0阶同调群是以域K的顶点为基的线性空间；还得出了有向图的无穷小余代数的0阶和1阶同调群是平凡的。对继续研究其他余代数的同调群具有指导意义。

［1］ Dourlens S. On the Hochschild Cohomology of triangular algebras［J］.Comm. Algebra，2008，31（10）:487-493.

［2］ 周伯壎.同调代数［M］.北京:高等教育出版社，2008.

［3］ Roos J E. Good and bad koszul algebras and their Hochschild Homology［J］.Pure and Appl. Algebra，2005，201（3）:295-327.

［4］ Liu S X，Zhang P. Hochschild Homology of truncated algebras［J］. London Math. Soc，1994，26（13）:427-430.

［5］ 刘海成. 三角几何余代数的Hochschild 同调群的计算［J］.苏州大学学报，2012，28（3）:6-10.

［6］ 刘海成. 多项式余代数的Hochschild 同调群的计算［J］.黑龙江八一农垦大学学报，2012，24（4）:85-87.

［7］ Jacobson N. Abstract derivation and lie algebra［J］. Trans AMS，2007，42（2）:206-224.

［8］ Doi Y. Homological Coalgebra ［J］. Math .Soc. Japan，1981，33（1）:31-51.