水平轴海流能发电机叶片设计与性能分析

何煜平，杨建民

(上海交通大学 海洋工程国家重点实验室，上海 200240)

所谓海流，是风应力、密度梯度、引潮力等作用而形成的大规模相对稳定的流动。据统计，全球海流能蕴藏总量接近于3.5TW［1-2］。若能合理地将这些能源加以利用，则能为缓解能源危机提供一条新的道路。

海流能发电的方式类似于风能发电，从概念上来说都是利用流体产生的升力或者阻力使获能装置运动，并带动内部的发电机发电。与风能相比，海流能发电具有以下的优势:1)海水密度是空气密度的830 倍，使得海流能具有比风能更大的能量密度;2)海流，特别是潮流，其流向和流量相对稳定并且容易预测［3-4］。

目前，海流能技术最为先进、产业化进程最为顺利的国家为英国。2008年4月，英国MCT 公司完成了1.2 MW 的水平轴海流机发电装置“SeaGen”的安装和运营，标志着世界上第一个商业化规模的海流发电系统投入使用［2］。国内的部分学校和研究所也都在积极开展海流能发电的研究，但尚处于起步阶段。

目前海流能领域的研究热点主要集中在以下方面:1)海流机叶片的水动力设计方法;2)叶片可调距机构的设计;3)安装与支撑方式的设计研究;4)叶片气蚀的研究和抑制;5)机组布局的研究;6)海流能发电装置新概念的设计［2-4］。

本文利用了叶素－动量理论［5-6］，对给定额定工况的海流能发电机的叶片进行了设计，并分别利用理论方法和CFD 方法对叶片的水动性能进行了计算和分析。

1 叶素－动量(BEM)理论

叶素－动量理论是同时利用动量定理和叶素理论进行叶片水动力外型设计的方法。若叶轮远前方流速为U1，远后方流速为U2，叶轮转速为Ω，旋转尾流角速度为ω，可定义轴向诱导因子a 和周向诱导因子b:

由动量定理，叶轮受到的轴向力T 和转矩M 等于单位时间内通过叶轮的流体动量和角动量的变化量。对于叶轮上一个半径为r、宽度为dr 的圆环，其受到的轴向力dT 和转矩dM 可表示为:

叶素理论则是将叶片沿径向分成若干叶素，对每个叶素分别进行分析，然后将作用在每个叶素上的力叠加，得到整个叶轮上的流体作用力。位于半径r 处叶素的速度和受力情况如图1 所示。

叶素上的流体相对速度U 为:

叶轮旋转面与流体相对速度之间的夹角φ 为:

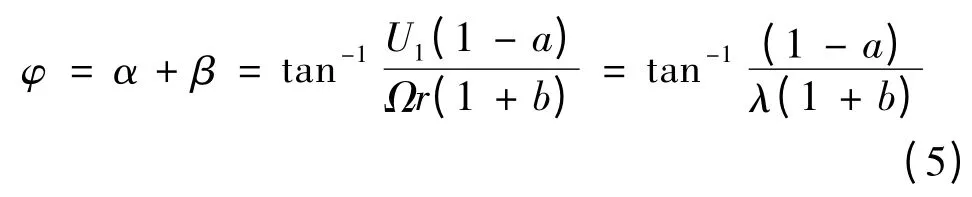
式中:α 为攻角;β 为扭角;λ 为局部速度比，λ =Ωr/U1，其中叶尖处局部速度比称尖速比，记为λ0。

设在攻角α 下，翼型的升力系数和阻力系数分别为CL和CD。则对于弦长为c，宽度为dr 的叶素，其受到的升力dL 和阻力dD 可分别表示为:

若叶片数为N，则半径为r、宽度为dr 的叶轮圆环上受到的轴向力dT 和转矩dM 可以表示为:

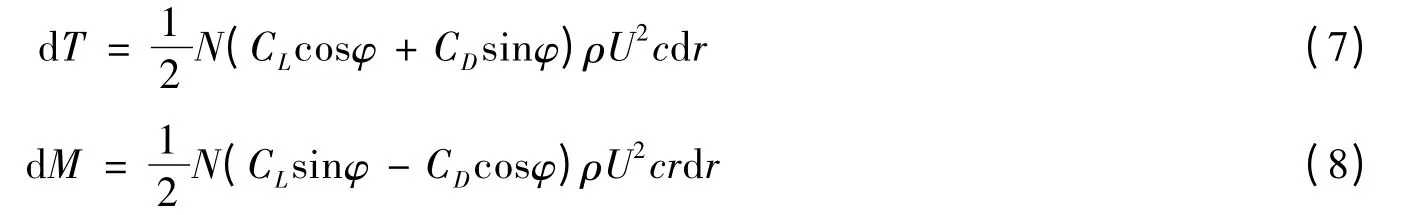
令式(2)和式(7)相等，式(3)和式(8)相等，可得

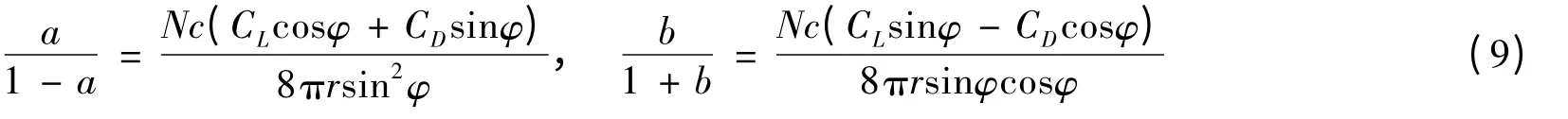
Tony Burton 通过比较考虑阻力和忽略阻力两种情形下的最优叶片设计，发现阻力对叶片的最优设计影响很小［5］。因此，忽略叶片阻力，则式(9)变为:

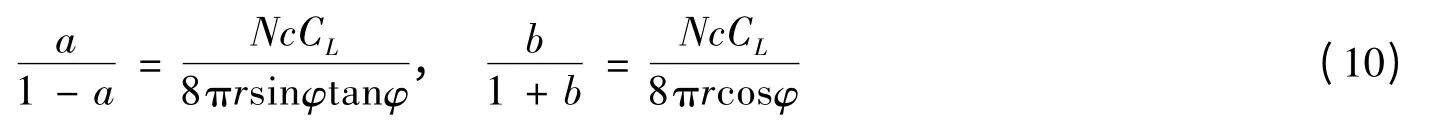
根据式(5)和式(10)，得到a、b 和λ 三者之间的关系:

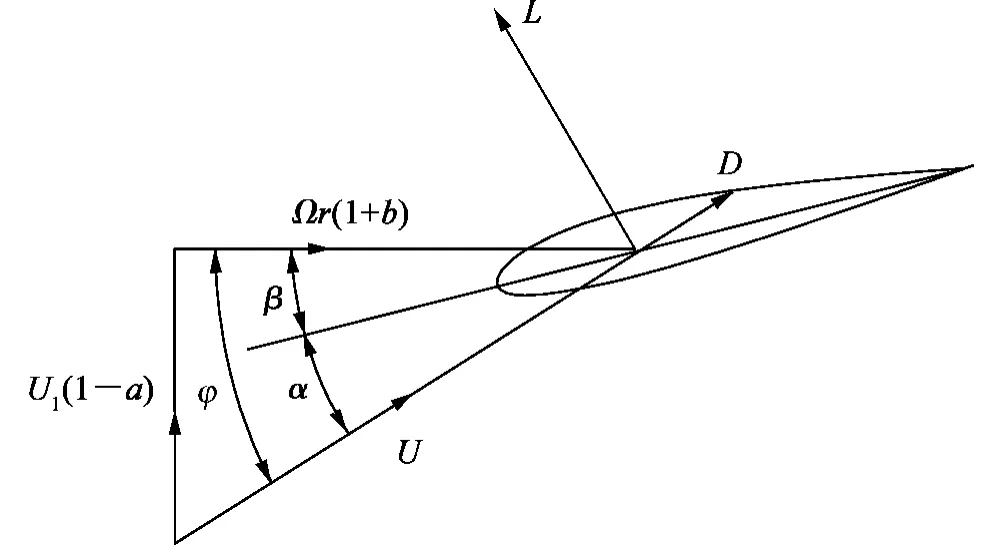
图1 叶素的速度和作用力分析Fig.1 Velocities and forces of a blade element

2 基于BEM 理论的海流机叶片设计

2.1 基本设计步骤

表征海流机叶片性能的参数主要包括推力系数CT、转矩系数CM和获能系数CP:

海流机叶片水动力外形设计，是在确定的设计流速U1、尖速比λ0和输出功率P0的条件下，使叶片的获能系数CP尽可能大。设计时，需要首先确定叶片数目N、叶轮半径R、叶毂半径RH，并选定合适的翼型。目前比较常见的叶片数主要有2 叶和3 叶。叶片数越多，获能系数CP越大，但轴向力系数CT也随之大幅提高，对支撑系统的设计有较高的要求。叶轮半径R 可以通过下式估算:

式中的获能系数CP是通过经验确定的预估值。叶毂半径RH可根据设计经验，取叶轮半径合适的百分数。叶片翼型的选取可以参照各翼型的水动力性能曲线，选取最大升阻比L/Dmax较大的翼型，同时还需保证具有较好的失速特性。通常叶尖处翼型较薄，叶根处翼型较厚，并逐渐过渡为轮毂处的圆形截面。

确定了上述设计参数后，可利用BEM 理论确定弦长c 和扭角β 沿叶轮径向的分布。步骤如下:

1)选取一控制截面，其径向位置为r。计算局部速度比λ=Ωr / U1。

2)确定a 和b，使获能系数CP最大。根据式(8)，叶轮圆环处的功率可表示为:

因此，(1 －a)b 的取值越大，dP 就越大。但是，a、b 和λ 三者之间受到了式(11)的约束。为了确定a 和b 的最优值，需要求解以下单目标带约束的非线性优化问题:

3)根据控制截面处翼型升力系数曲线，找到对应最大升阻比的最优攻角α 以及相应的升力系数CL。

4)根据式(5)确定φ，则扭角β=φ－α。根据式(9)确定弦长c。

5)重复步骤1)～4)，直到所有控制截面计算完毕。

2.2 翼型水动力性能

在叶片设计时，需要叶片截面翼型的升力系数曲线和阻力系数曲线作为输入参数。对于NACA 翼型族相关性能曲线，可通过XFoil 等翼型分析软件获得，也可通过CFD 方法求得［7］。本文所使用的翼型性能曲线是通过Fluent 软件求得，其中NACA 2414、NACA 2416 和NACA 2418 翼型的升力系数曲线和阻力系数曲线如图2 所示。翼型失速角约为16°到18°，最大升阻比对应的最佳攻角约为7°。

图2 NACA 24 系列翼型升力系数和阻力系数曲线Fig.2 Lift coefficient and drag coefficient curves of NACA 24 series

2.3 150 kW 水平轴海流机叶片设计实例

设有如表1 所示的设计要求，利用BEM 理论进行水平轴海流机叶片的设计。设计时，为了简化问题，认为海流机所处水深较深，海流不受自由表面波浪的影响，且认为海流流速在整个叶轮处均匀分布。由于海流相对比较稳定，在通常情形下流速能保持在较小范围内浮动，因此设计流速可以从该流速范围内选取。

表1 海流机叶片设计参数Tab.1 Parameters of blade designing of a current turbine

取获能系数预估值为0.4，根据式(13)计算叶片半径，得R≈5.5 m。叶片翼型选取NACA 24 系列，叶根处为了保证足够的结构强度，选取叶片厚度t 为18%，然后向叶尖处逐渐过渡为16%和14%。利用前述设计步骤计算截面弦长c 和扭角β，c 和β 沿着叶轮径向的分布曲线如图3 所示。利用Pro/E 进行叶片实体建模，如图4 所示。

图3 150 kW 海流机叶片几何参数径向分布Fig.3 Radial distribution of geometric parameters of the 150 kW current turbine's blade

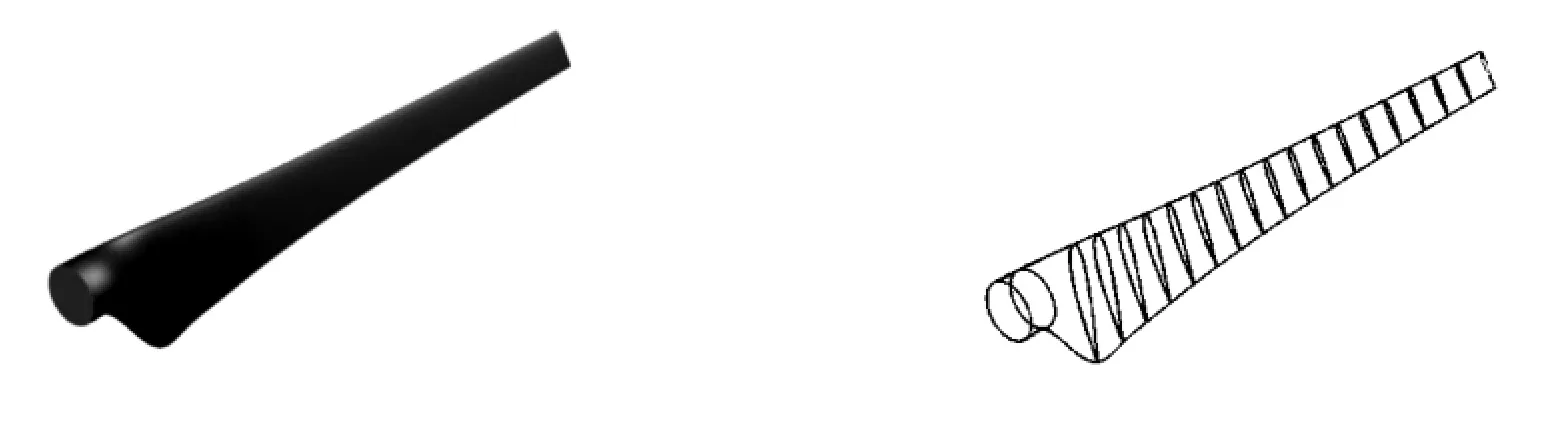
图4 150 kW 海流机叶片实体模型Fig.4 Model of the 150 kW current turbine's blade

3 海流机水动力性能计算

为了检验叶片设计是否合理，以及预测不同工况下的性能，需对海流机的水动力性能进行计算。BEM理论结合普朗特(Prandtl)修正以及葛劳渥(Glauert)修正是较常用的海流机水动力性能理论计算方法［5-6］。

3.1 Prandtl 叶尖/轮毂损失修正

叶素-动量理论忽略了顺着翼展方向的速度分量，然而实际上水流在叶片上存在着径向流动。尤其在叶尖和轮毂处，这种三维流动效应更是明显，因此叶尖损失和轮毂损失对叶片性能的影响不容忽略。Prandtl针对该现象提出了Prandtl 渐进法。根据该理论，叶尖损失和轮毂损失可用损失因子Ft(r)和Fh(r)来表示:

总的损失因子F (r)可表示为:

经过修正后的轴向诱导因子a 和轴向诱导因子b 的表达式变为:

3.2 Glauert 轴向诱导因子修正

当轴向诱导因子a 较大时，根据动量定理，叶轮后方的尾流速度将很低，甚至发生反向。实际上这种情况不可能发生，取而代之发生的是尾流变成了湍流，而动量定理不再适用。同时通过混合过程，湍流尾流从周围流体中重新获得能量。针对这种现象，Glauert 提出了一种利用经验公式对a 进行修正的方法:

3.3 海流机水动力性能理论计算步骤

利用BEM 理论进行海流机水动力性能计算的步骤如下:

1)确定计算工况:流速U1、尖速比λ0、桨距角β0。

2)选取计算截面。该截面翼型弦长为c(r)，扭角为β(r)。

3)对截面轴向诱导因子a 和周向诱导因子b 赋初值。可令a0= 0，b0= 0。

4)利用式(5)计算确定φ，则攻角α = φ － β(r)－ β0。

5)利用攻角α 查得升力系数CL和阻力系数CD。利用式(16)和(17)计算损失因子F(r)。利用式(18)对a0和b0进行修正，修正后的轴向诱导因子和周向诱导因子记为a 和b。

6)判断a 是否大于0.38。若a 大于0.38，利用式(19)对a 进行修正。若不满足，则直接进入步骤g。

7)计算Δa= |a－a0|和Δb= |b－b0|。判断Δa 和Δb 是否小于收敛精度ε:若满足，进入步骤h;否则令a0=a，b0=b，并重复步骤c 至步骤g，直至收敛。

8)利用式(4)和式(5)计算U 和φ，然后利用式(7)和式(8)计算截面dT/dr 和dM/dr。

9)判断是否所有计算截面计算完毕:若满足，进入步骤10;否则，选取新的计算截面，返回步骤2。

10)对各个截面求得的dF 和dM 进行积分，求得轴向推力T 和转矩M，捕获的功率P =MΩ。为了便于比较不同尺寸海流机的性能，对载荷与功率进行无因次化，求得推力系数CT、转矩系数CM和获能系数CP。

3.4 海流机水动力性能计算结果与分析

利用BEM 理论，对所设计的150 kW 水平轴海流机在定桨距运行状态和变桨距运行状态下的水动力性能分别进行了计算。

3.4.1 固定桨距

设海流机叶片桨距角β0固定为0°，来流U1保持为2 m/s 不变，计算不同尖速比λ0下海流机的水动力性能。图5 和图6 所示的是不同尖速比λ0下，α、dCT/dr 和dCM/dr 沿叶片径向的分布情况。其中dCT/dr 和dCM/dr 为无因次化的单位长度叶片推力和转矩，定义为:

图5 不同尖速比下攻角径向分布Fig.5 Radial distribution of attack angle under different tip speed ratios

由图5 可知，随着尖速比λ0的增大，叶片的攻角随之减小。当λ0等于2 或3 时，整个叶片的攻角均大于失速角，叶片工作于失速状态中。当λ0等于6 时，即处于设计尖速比时，整个叶片的攻角基本处于6°到8°之间，接近于翼型最大升阻比对应的最佳攻角。此外，由于叶尖损失的影响，导致叶梢处的攻角明显减小。

由图6 可知，随着尖速比λ0的增大，叶片产生的轴向推力也增大，最大转矩则出现在尖速比λ0等于4附近。当λ0等于2 或3 时，推力分布曲线与转矩分布曲线的变化趋势不同于λ0较大时的情况，这是由叶片失速所导致。当λ0增大时，叶尖处首先离开失速状态，因此叶片载荷分布也由叶尖处开始逐渐恢复正常。对于正常工作的叶片，在同一尖速比λ0下，最大推力出现在r =5.00 m 附近，最大转矩出现在r =4.75 m附近。

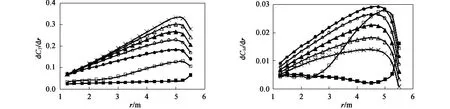
图6 不同尖速比下推力和转矩径向分布Fig.6 Radial distribution of thrust force and torque under different tip speed ratios

图7 CT、CM 和CP 随尖速比λ0 变化曲线Fig.7 Curve of CT，CM and CP to λ0

图7 所示的是水平轴海流机推力系数CT、转矩系数CM和获能系数CP随着尖速比λ0变化的曲线。如前文所述，随着尖速比λ0增大，推力系数CT增大。转矩系数CM在λ0=4 时取得最大值CMmax=0.092。而获能系数CP则在设计尖速比λ0=6 时取得最大值CPmax=0.420，且在λ0=6 附近CP数值变化幅度相对较小。说明利用BEM 理论进行水平轴海流机叶片的设计基本能实现预期要求。

3.4.2 可变桨距

图8 不同桨距角下CP 随尖速比λ0 变化曲线Fig.8 Curves of CP to λ0 with different pitch angles

叶片设计完毕之后，叶片截面的各项参数也随之确定，因此在相同的工况下，定桨距海流机的水动力性能也是确定的。对于变桨距海流机，则可以通过调节叶片的桨距角β0改变来流攻角以调节叶片的水动力性能，从而实现过载功率控制、提高启动转矩等要求［8］。

图8 所示的是桨距角β0为0°、±5°和±10°时，获能系数CP随尖速比λ0变化的曲线。可以发现，当叶片运行在低尖速比条件下时，正的桨距角能提高装置的获能系数CP，而负的桨距角将减小装置的获能系数CP。而当叶片运行在高尖速比条件下时，无论正的桨距角还是负的桨距角，都将减小装置的获能系数CP。桨距角越大，对获能系数CP的影响越是明显。另外，正的桨距角下获能系数曲线较为平坦，负的桨距角下获能系数曲线则比较陡峭，说明运行在负桨距角下的叶片对尖速比λ0的变化较为敏感。

4 基于Fluent 的水平轴海流机性能计算

除了使用相关理论计算海流机水动力性能之外，利用CFD 方法对海流机进行数值计算也是验证设计结果的重要方法。本文使用Fluent 软件，利用多重参考系(MRF)模型［9］模拟了海流机在均匀来流U1、固定桨距β0、不同尖速比λ0下的工作情况。

4.1 计算模型

在进行数值计算前，首先使用Gambit 软件建立数值计算模型，划分计算网格。

计算模型如图9 所示。整个流场划分为两个相嵌套的圆柱形流体区域A 和B。其中区域A 是固定区域，长150 m，半径50 m，左侧底面的边界条件设置为速度入口(velocity inlet)类型，右侧底面和侧面边界条件设置为出流(outflow)类型。区域B 是旋转区域，长10 m，半径10 m，两个区域的接触面设置为交界面(interface)类型。海流机叶片位于较小的圆柱形流体区域B 中，设置为壁面(wall)类型，并将随着区域B 一起转动。

图9 水平轴海流机水动力性能数值计算模型Fig.9 Numerical model of horizontal axis current turbine

4.2 数值计算结果与分析

本文计算模拟了150 kW 水平轴海流机在固定来流U1=2 m/s，不同尖速比λ0下的工作情况。

图10 所示的是额定工况(U1=2 m/s，λ0=6)下海流机叶片的迎流面和背流面的压力分布等值线。可以发现，叶片迎流面为高压区，背流面为低压区，且这种压力差在叶尖处尤为明显。

图11 所示的是额定工况(U1=2 m/s，λ0=6)下叶轮(y=0 m)近后方截面(y= + 0.2 m)的流体合成速度等值线云图。从径向来看，随着半径的增大，流体的合成速度首先逐渐减小，说明叶根处吸收的流体动能较少，叶尖处吸收的流体动能较大。当半径增大到靠近叶稍处时，由于叶尖损失现象，流体动能的吸收率相对减小，故流体合成速度有所增大。

图12 比较了利用BEM 方法与CFD 方法计算获得的获能系数曲线。可以发现，利用CFD 方法计算获得的获能系数曲线峰值同样位于设计尖速比λ0=6 时，再次验证了水平轴海流机叶片设计方法的有效性。通过CFD 方法计算求得的获能系数最大值CPmax=0.372，为BEM 方法计算所得值的88.6%。

图10 额定工况下海流机叶片压力分布等值线Fig.10 Pressure contour of current turbine under rated condition

图11 额定工况叶轮近后方速度等值线云图Fig.11 Velocity contour behind the turbine under rated condition

图12 BEM 理论与CFD 方法CP 曲线比较Fig.12 Comparison of CP curves by BEM and CFD methods

5 结 语

叶片的获能系数CP决定了水平轴海流机的发电效率，叶片设计的目标就是使其获能系数CP尽可能大。BEM 理论是用于海流机叶片水动力外型设计的常用方法。通过使用BEM 理论结合普朗特修正和葛劳渥修正的理论计算方法以及CFD 方法，分别对150 kW 水平轴海流机的水动力性能进行了计算，两种方法的结果都表明该海流机的最大获能系数CPmax位于设计尖速比处，说明本文的叶片设计方法是有效的。

通过对以上两种方法的计算结果进行分析，发现叶片从海流中截获的能量和受到的载荷主要集中在叶尖区域，但是由于叶尖损失的原因，叶梢处吸收的能量和受到的载荷有明显的下降。另外，桨距角对海流机水动力性能的影响明显，通过调节桨距角可以实现海流机的功率和载荷控制。

［1］Blunden L S，Bahaj A S.Tidal energy resource assessment for tidal stream generators［J］.Journal of Power and Energy，2007，221(2):137-146.

［2］刘美琴，仲 颖，郑 源，等.海流能利用技术研究进展与展望［J］.可再生能源，2009，27(5):78-81.

［3］Ponta F L，Jacovkis P M.Marine-current power generation by diffuser-augmented floating hydro-turbines［J］.Renewable Energy，2008，33 (4):665-673.

［4］李 伟，林勇刚，刘宏伟，等.水平轴螺旋桨式海流能发电技术研究［C］∥中国可再生能源学会海洋能专业委员会第一届学术讨论会文集.2008:81-90.

［5］Burton T.风能技术［M］.北京:科学出版社.2007:37-55.

［6］马 舜，李 伟，刘宏伟，等.水平轴潮流能发电系统能量捕获机构研究［J］.机械工程学报，2010，46(18):150-156.

［7］王 立，董志勇，韩 伟，等.海流能转换器叶片翼型的失速和水动力特性的数值研究［J］.水动力学研究与进展:A辑，2011，26(1):58-64.

［8］马 舜，李 伟，刘宏伟，等.海流能发电系统的最大功率跟踪控制研究［J］.太阳能学报，2011，32(4):577-582.

［9］Wang J，Muller N.Performance prediction of array arrangement on ducted composite material marine current turbines (CMMCTs)［J］.Ocean Engineering，2012，41:21-26.