半潜型风机浮式基础设计及幅频运动特性研究

曹 菡，唐友刚，陶海成，秦 尧

(1. 天津大学 建筑工程学院，天津 300072;2. 天津大学 水利工程仿真与安全国家重点实验室，天津300072)

风力发电日益成为新能源中最具开发条件和最有发展前景的发电方式［1］，也因此引起了世界上众多国家的重视。我国风能资源丰富，仅近海的风能资源就是陆上风电可开发量的三倍，因此海上风力发电日益成为一种具有战略意义的新能源形式。为适应海上风电的发展，本文提出了一种半潜型浮式风机基础，并对其稳性及水动力特性进行了研究。

1 半潜型浮式基础概念设计

1.1 浮式基础模型参数

浮式风机主要包括两部分［2］:发电机组系统和支撑体系。发电机组系统包括发电机组、轮毂、叶片等。支撑体系包括上部的塔柱及其下部的浮式基础。发电机组与叶片通过轮毂与塔柱连接在一起，塔柱底部通过法兰和基础相连。由于半潜型基础的水线面由多个距离较远的小水线面构成，具有较大的水线面惯性矩，因而稳性好。本文以美国可再生能源研究所(NREL)公布的5MW 风机模型为例［3］，概念性地设计了一种半潜型浮式基础。

1.1.1 浮式基础主要设计参数

考虑水深为120 m，风速为11.4 m/s，风机发电功率为5 MW，设计浮式基础。

在立柱下缘设计大尺度的正六边形压水板，以增加风电系统的附加质量和阻尼［4］，抑制基础的运动。

在三个立柱内设计出压载舱，在基础底部的压载舱内采用混凝土压载，以降低基础重心和提高基础稳性。三个立柱的底面中心位于等边三角形的三个顶点上，三角形的边长为46 m。主要设计参数如表1 所示。

表1 浮式风电基础设计主尺度Tab.1 Main scale of the floating foundation

表2 海上5MW 风机整体模型重量参数Tab.2 Main weight parameters of the overall model

1.1.2 浮式基础主要重量参数

发电系统和浮式基础的主要参数如表2所示。

风机系统整体模型如图1 所示。

1.2 计算分析理论

1.2.1 风载荷

1)叶片载荷

图1 整体模型Fig. 1 Overall model

叶片载荷是风机工作中的重要载荷，一般采用动量-叶素理论进行计算。首先将叶片沿展向分成许多微段，称这些微段为叶素，每个叶素上的流动相互之间没有干扰，叶素可以认为是二元翼型，运用动量理论求出作用在这些叶素上的力和力矩，然后沿叶片展向积分，进而求得作用在整个叶轮上的力和力矩。作用在每个叶素上的推力和弯矩为:［5］

式中:ρ 为空气密度，W 为合成风速，B 为风轮的叶片数，C 为叶素剖面弦长，Cl、Cd分别为每个叶素的升力系数和阻力系数，φ为入流角，r 为叶素与轮毂中心的距离，δr 为每个叶素的展向长度。

2)塔柱载荷

塔柱风载荷的计算依据CCS 规范得到其表达式［6］:

式中:Ch为受风构件高度系数，Cs为受风构件形状系数，Ai(α)为风向角为α 时第i 个受风构件在风向上的投影面积，v 为风和结构物的相对速度。

由于塔柱的直径是渐变的，故在计算塔柱上的风载荷时，将塔柱自水线面至轮毂处分为9 段，分别计算各段上的风载荷。

3)风倾力矩

根据CCS 规范，得到计算风倾力矩的公式［6］

式中:i 为受风结构的序号，n 为受风结构的个数，Fi为受风构件上的风载荷，Zi为受风面积压力中心至水下侧向阻力中心间的垂直距离。

在具体计算中，分别考虑叶片载荷、塔柱载荷以及水线面以上立柱所受风载荷，然后使用excel 列表计算不同高度处构件的风倾力矩，而后求和。

1.2.2 波浪载荷

由于该半潜型浮式基础的连接构件属于小尺度构件，而面元模型属于大尺度构件，故采用两种波浪理论计算其波浪载荷。

用Morison 公式计算小尺度构件(即浮式基础的Morison 模型)上的波浪载荷［6］:

式中:ρ 为海水密度，CM和CA分别为惯性力系数和附加质量系数，CD为拖曳力系数，u 和u·分别为垂直于构件轴线的水质点速度和加速度，x·和 x··分别为垂直于构件轴线的构件速度与加速度。

大尺度构件(即浮式基础的面元模型)上的波浪载荷按照三维线性势流理论计算。将速度势φ 分解为入射势φI、绕射势φD和辐射势φR。其中:

式中:g 为重力加速度，A 为波幅，K 为波数，d 为水深，β 为波向角。

φD和φR采用边界单元法求解，首先把物体表面离散成许多单元，然后假定每个单元内部的速度势可以用单元节点势的函数表达，利用配点法或伽辽金方法等建立节点势的线性方程组，最后求出各节点处的速度势。根据线性化的伯努利方程，求出波浪对结构物的作用力［4］。

1.2.3 粘性阻尼

浮式基础的水平撑、斜撑及压水板为基础运动提供很大的粘性阻尼，将会有效拟制浮体的共振运动。由于SESAM 程序中采用势流理论，无法计及粘性阻尼的影响，这与实际情况差异很大。本文在RAOs 计算时，考虑了粘性阻尼的作用，计算得到等效的6 ×6 粘性阻尼矩阵，文中只保证垂荡、横摇和纵摇在对角线上的值非零，而不考虑其它运动方向的耦合。关于浮式基础粘性阻尼的计算，目前还缺乏成熟的方法。本文依据文献［7］提供的方法，计算浮式基础的粘性阻尼。

等效粘性阻尼可视为临界阻尼的一部分，临界阻尼β0按照下式计算［7］:

式中:M 表示结构质量或结构惯性矩，Ma表示结构附加质量，Ci表示结构静水回复力刚度。对于半潜型浮式基础的粘性阻尼，文献［7］认为可取为临界阻尼的10%，并通过实验研究进行了验证。由于本文的浮式基础在形式上与文献［7］相同，故也取粘性阻尼为临界阻尼的10%。半潜型浮式基础垂荡、横摇、纵摇三个自由度的临界阻尼计算结果如表3 所示。

表3 临界阻尼的计算结果Tab.3 Computation of critical damping

1.2.4 频域运动方程以及传递函数

频域运动方程以及传递函数为:

式中:ω 为入射波角频率;β 为入射波传播方向;M 为浮体惯性矩阵;A(ω)为附加质量矩阵;B(ω)p为辐射阻尼矩阵;Bv为粘性阻尼矩阵;C 为静水回复力矩阵;Ce为系泊系统的回复力矩阵;X(ω，β)为浮体运动矩阵;F(ω，β)为波浪激励力矩阵，由作用在大尺度构件上的波频力和作用在小尺度构件上的惯性力以及拖曳力组成。在初步设计阶段，忽略了Ce的作用。

在简谐波作用下，随时间变化的浮体响应可写为［8］:

式中:A 为入射波波幅;ω 为入射波的角频率;β 为入射波的传播方向;t 为时间;H(ω，β)为传递函数或响应幅值算子，简记为RAOs。

2 稳性分析

采用SESAME 进行稳性计算。考虑不同方向风载荷的作用，计算风倾力矩，限于篇幅，文中仅给出最危险情况的稳性计算结果。

图2 稳性分析模型Fig. 2 Model of stability analysis

浮式风机上部结构距离水面76 m，机舱、塔架及叶片总重量为690 t。设计的浮式风机基础立柱高32 m，将每个立柱自下至上划分为三层，高度依次为10、11 及11 m，然后每层又被横纵舱壁分隔为四个舱室，即每个立柱划分为12 个舱室。建立的稳性分析模型如图2 所示。

2.1 完整稳性

完整稳性主要考察平台倾斜后产生的复原力矩阻止其倾覆的能力，并着重研究复原力矩随横倾角变化的规律。

对于半潜型平台，平台回复力矩曲线第二交点或进水角(取较小者)以下的面积(A +B)与风压倾覆力矩曲线的同一限定角以下的面积(B +C)之比(如图3所示)应满足以下要求［6］:(A+B)/(B+C)≥1.3。

图4 所示为风机在额定风速下正常工作时的完整稳性计算结果，计算时考虑了不同风向的影响，这里仅给出最大风倾力矩的稳性核准结果。由图4 曲线可知，复原力矩曲线与风倾力矩曲线的第一交角为4.56°，甲板处进水角为14.79°，平台复原力矩曲线进水角以下的面积与风倾力矩曲线的同一限定角以下的面积比为1.71，满足规范要求，且复原力矩在正浮到进水角的所有角度范围内均为正，故完整稳性满足海洋平台规范要求。

图3 回复力矩与倾覆力矩曲线Fig. 3 Righting moment and overturning moment curves

图4 完整稳性结果Fig. 4 Result of intact stability

2.2 破舱稳性

理论上平台在破损情况下也应具有足够的回复能力。破舱稳性就是研究平台在一舱或多舱破损情况下平台的复原力矩随横倾角的变化情况。

由于本计算中风向沿X 轴正向，风机基础倾斜轴为Y 轴。经分析，X 轴正向的立柱会先入水，所以在计算破舱稳性时选择该立柱上的舱室破损。

因为水线面处舱室容易破损，所以一舱破损时选择图中Cm_LC4 破损(见图2 立柱顶部舱室)，其复原力矩的变化情况如图5 所示。

由图5 可以看出，当横倾角达到进水角时，复原力矩为1.964 ×108，随后急速减小到1.457 ×108，然后在较小的回升后保持平稳。整体来看复原力矩仍远大于风倾力矩，故浮式基础在一舱破损时的稳性有保证。

两舱破损时，选择Cm_LC3 与Cm_LC4(见图2)进水，其计算结果如下:

图5 Cm_LC4 破舱稳性Fig. 5 Damaged stability of Cm_LC4

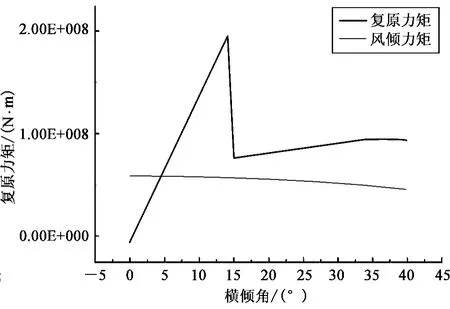
图6 Cm_LC3，Cm_LC4 破舱稳性Fig. 6 Damaged stability of Cm_LC3 and Cm_LC4

由图6 可见，当横倾角大于进水角后，由于舱室破损进水，复原力矩减小的速度比一舱破损时更快，在横倾角约为15°时，其值为7.697 ×107，随后有所回升，但幅度不大。而从整体来看，仍可保证浮式基础稳性满足规范要求。

3 频域运动响应计算分析

3.1 幅频响应曲线(RAOs)

文中选取的坐标系:Z 轴竖直向上且与塔柱的中心轴重合，零点位于水线面处;X 轴和Y 轴零点位于塔柱中心。坐标系的原点位于三立柱中心构成的三角形的外接圆圆心处，模型整体关于X 轴对称，建立的面元模型和Morison 模型如图7 和图8 所示。

图7 面元模型Fig. 7 Pannel model

图8 Morison 模型Fig. 8 Morison model

在进行频域分析时，建立了包括风机、塔柱、基础在内的水动力分析模型。为较为精确地显示结构的运动性能，添加了粘性阻尼矩阵。该半潜型浮式基础的工作水深为120 m，选择的波浪周期范围为2 ～60 s，时间间隔为2 s，波高为2 m，得到该半潜型浮式基础的幅频响应曲线图(RAOs)。垂荡、横摇及纵摇三个自由度的幅频响应曲线如图9 ～图11 所示。

图9 垂荡RAOsFig. 9 RAOs of heave

图10 横摇RAOsFig. 10 RAOs of roll

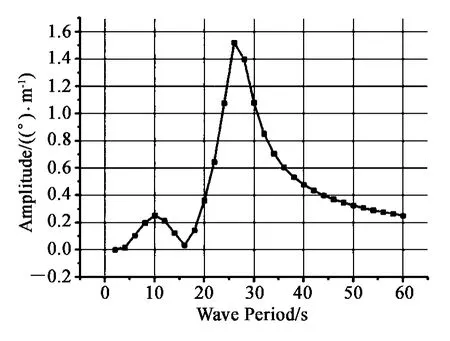
图11 纵摇RAOsFig. 11 RAOs of pitch

由图9、图10、图11 幅频响应曲线可以看出，在垂荡自由度上，浮式基础在波浪周期小于20 s 时运动幅度较小，周期26 s 时为1.375 m，基础在短周期波浪(高频)区域运动幅值较小，在长周期波浪(低频)区域幅值趋于1 m，随波浪周期的增大运动响应变化比较迟缓;在横摇自由度上，基础在26 s 时运动响应达到最大，为1.203°，在波浪周期小于20 s 时浮式基础横摇较小;在纵摇自由度上，基础在26 s 时运动响应达到最大，为1.522°，在其他波频区域运动响应较小。由于本文考察的海况条件大部分能量集中在周期为4 ～20 s 的范围内，因此所设计的浮式风电系统的运动基本上可以避开主要的波能周期段，进而可以有效地控制浮式基础的运动响应。

3.2 不同浪向角对基础运动响应的影响

改变波浪的方向，计算幅频运动响应，研究浪向对于浮式基础运动的影响，详见图12 ～图14。

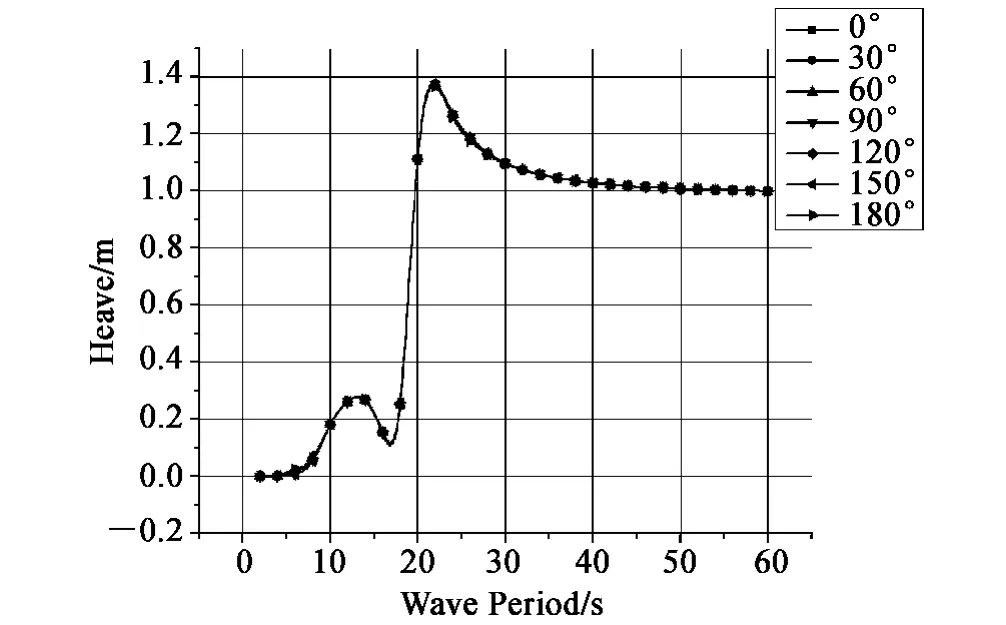
图12 不同浪向角下的垂荡RAOsFig. 12 RAOs of heave in different wave angles

图13 不同浪向角下的横摇RAOsFig. 13 RAOs of roll in different wave angles

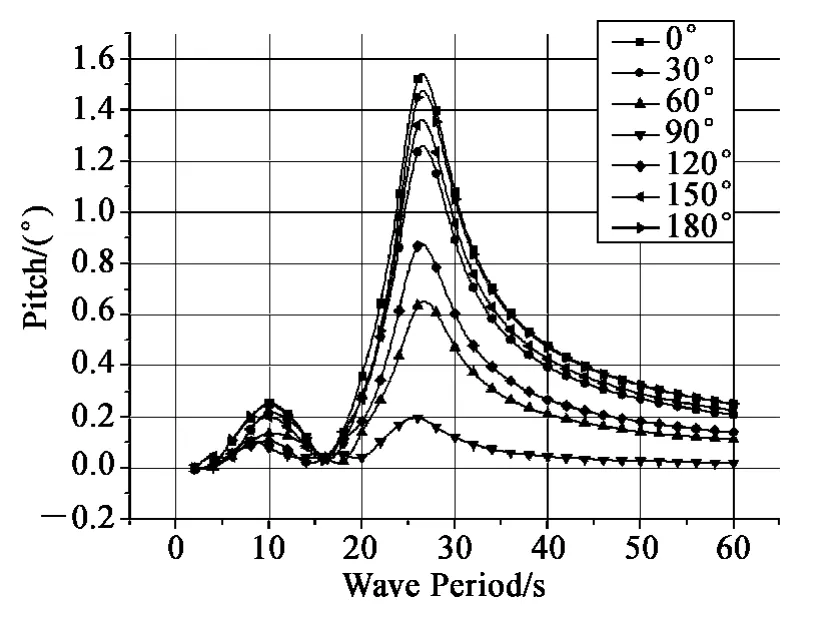
图14 不同浪向角下的纵摇RAOsFig. 14 RAOs of pitch in different wave angles

由上面不同波浪入射角的幅频响应曲线可以看出:垂荡自由度在不同入射角下运动响应基本一致，基础垂荡自由度的运动响应受波浪入射角的影响较小;基础在横摇与纵摇自由度的运动响应受波浪入射角的影响较大，横摇在波浪入射角为90°时运动响应最大，在波浪入射角为0°时运动响应最小;纵摇在波浪入射角为0°时运动响应最大，在波浪入射角为90°时较小。

4 结 语

进行了半潜型浮式基础的概念设计，初步分析其完整稳性及破舱稳性，考察了结构在频域范围内的运动特性，通过对结果的分析，得出以下结论:

1)半潜型基础的水线面由多个距离较远的小水线面构成，具有较大的水线面惯性矩，这些结构特征决定了它较之其他形式的结构基础具有相对较好的稳性。在正常工作状况下，使用动量-叶素理论计及叶片产生的气动载荷，在较大的风倾力矩作用下，基础仍具有良好的回复能力，其完整稳性满足规范要求。

2)当一舱或两舱破损时，复原力矩仍大于风倾力矩，基础不会倾覆，但复原力矩曲线出现尖角，其值出现急剧下降趋势。

3)设计的浮式基础具有良好的水动力特性，考虑粘性阻尼的作用，其垂荡、横摇和纵摇响应均比较小，并且能够避开主要的波能周期范围。改变波浪方向，对垂荡自由度的影响不大，横摇纵摇所受影响较为突出。

［1］高 坤，李 春，高 伟，等.新型海上风力发电及其关键技术研究［J］.能源研究与信息，2010，26(2):110-116.

［2］严 磊.风力发电机支撑体系结构设计研究［D］.天津:天津大学，2008:9-10.

［3］J Jonkman，S Butterfield，W Musial，et al.Definition of a 5-MW reference wind turbine for offshore system development［R］.Technical Report，NREL/TP-500-38060，2009.

［4］阮胜福.海上风电浮式基础设计与运动响应研究［D］.天津:天津大学，2010.

［5］李军向.大型风机叶片气动性能计算与结构设计研究［D］.武汉:武汉理工大学，2008.

［6］中国船级社.海上移动平台入级与建造规范［M］.北京:人民交通出版社，2005.

［7］Dominique Roddier，Antoine Peiffer，Alexia Aubault，et al. A generic 5MW windfloat for numerical tool validation ＆ comparison against a generic SPAR［C］∥Proceedings of the ASME 30th International Conference on Ocean，Offshore and Arctic Engineering. Rotterdam，2011:OMAE 2011-50278.

［8］余小川，谢永和，李润培，等.水深对超大型FPSO 运动响应与波浪载荷的影响［J］.上海交通大学学报，2005，39(5):674-677.

［9］张 亮，邓慧静.浮式风机半潜平台稳性数值分析［J］.应用科技，2011，38(10):13-17.