基于模糊PI 控制器SRM 的DITC 系统研究

王勉华，薛会强

(西安科技大学，陕西西安710054)

0 引 言

开关磁阻电机(以下简称SRM)具有结构简单、工作可靠、起动电流小、起动转矩高，调速性能优越等特点，在各种工业调速中广泛应用，成为交、直流调速电机的有力竞争者［1］。但是由于其双凸极结构使得电机存在非线性，进而产生电机输出转矩脉动。因此，如何从控制方法上减小SRM 转矩脉动已成为目前研究的热点。目前的控制策略主要有传统控制策略、神经网络学习控制、自适应模糊控制、变结构控制、转矩分配控制、迭代学习控制等。其中文献［2］中采用BP 神经网络自适应PID 控制器来调节静差，但其预测能力和训练能力的存在矛盾，而且学习精度依赖性高。文献［3］中提出了模糊PID 控制的调速系统，虽然可以使系统无静差，鲁棒性好，但控制器设计复杂，而且转矩脉动波动依然较大。

为了克服前面控制方法的不足，本文在分析SRM 特性的基础上提出了模糊PI 复合控制与直接瞬时转矩控制相结合的方法来减小转矩脉动。与传统方法不同的是，直接瞬时转矩控制是把任意时刻总的输出转矩作为控制量，使每一时刻的瞬时转矩来跟随参考转矩［4－5］。

1 SRM 的直接瞬时转矩控制系统结构

直接瞬时转矩控制(以下简称DITC)系统主要包括SRM 电机本体、模糊PI 调节器、不对称功率变换器模块、转矩滞环控制器和转矩估计单元等。系统控制框图如图1 所示。本系统采用两个闭环控制，内闭环是转矩环控制，作用是对转矩误差通过功率变换器来选择开关状态，从而控制开关元件的通断，为电机各相提供所需能量;外闭环采用速度环，作用是对转速进行调节进而得到内环的参考转矩给定。

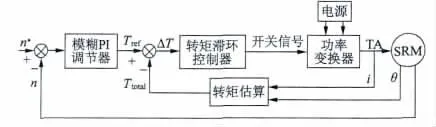
图1 SRM 的DITC 控制系统框图

2 SRM 力矩特性分析与控制器设计

DITC 原理是通过比较给定参考转矩与瞬时转矩的误差，在设定的开关角内，控制相绕组上电压开关状态来实现控制输出转矩的方法。通过下一相优先导通的原则来确定相邻两相转矩的分配规律。

2.1 SRM 的力矩特性分析

SRM 转矩是磁阻性质，其运行原理遵循 “磁阻最小原理”，因磁场扭曲而产生磁拉力。

在对SRM 性能作定性分析时，若忽略磁路的非线性，则相电流产生电磁的转矩可简化:

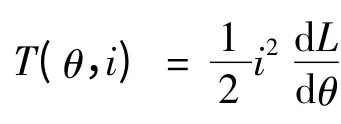
由上式可知，转矩方向与电流方向无关，仅取决于电感随转角的变化情况。如在电感上升区，相绕组通以电流时产生正转矩，处于电动机状态;而在电感下降区，通以电流则产生负转矩，处于发电机状态。所以，SRM 起动并连续运行的条件是转矩为正。在DITC 中，转矩是直接控制的量，而绕组相电压选择是由参考转矩给定与瞬时转矩之差决定［7］。而且按导通角的导通相数的不同分为两相导通和单相导通区域，如图2 所示。

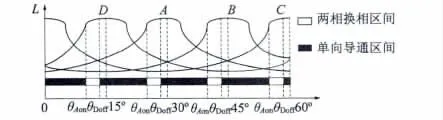
图2 各相电感与转子位置角关系

2.2 功率变换器的开关状态

施加在定子绕组上的空间电压矢量是由功率变换器的开关状态所决定的，瞬时转矩控制要合理选择的也就是功率变换器开关元件不同通断状态下所决定的定子绕组相电压状态。本设计功率变换器采用不对称半桥式结构。开关管有三种状态:1，0，－1。状态1:两个开关管同时导通，为绕组提供上正电压;状态0:一个开关管导通，为绕组提供零电压的续流过程;状态－1:两个开关管同时关断，为绕组提供上负电压［6］。如图3 所示。

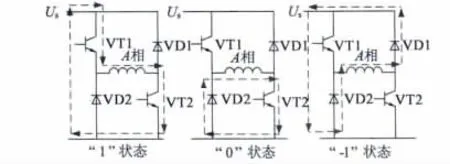
图3 SRM 开关状态

2.3 SRM 转矩滞环的设计

DITC 的核心是滞环控制器的设计。而在不同导通区域内滞环控制器的设计也有所不同，如图4所示。滞环在单相导通区域，此时有三种开关状态:1，0，－1。以A 相为例，当瞬时转矩减小，使转矩误差增加并超过ΔT1，则此时相绕组电压状态从0 变为1，为A 相提供正相电压使瞬时转矩增加。若瞬时转矩增大，使转矩误差减小至－ΔT1，此时开关工作于状态0，使A 相所加电压为零，减小瞬时转矩。

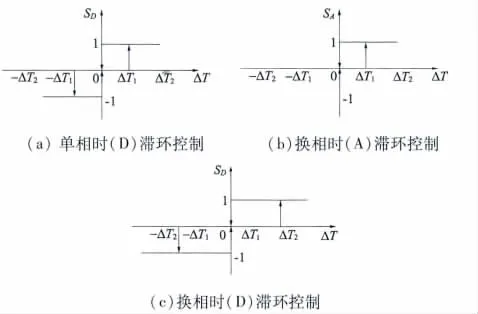
图4 DITC 转矩滞环控制器工作原理

两相同时导通为换相区，此时需内外滞环同时工作。以SRM 从A 相换相至B 相的过程为例。瞬时转矩为两相转矩之和，当转矩误差大于0 且增加至区间，则需增加输出转矩，此时A、B 相处于状态0 为续流阶段。当转矩误差增加至区间ΔT2＞ΔT ＞ΔT1，则B 相绕组要进入状态1，A 相依然保持续流状态0。当转矩误差增加超过外滞环区间ΔT ＞ΔT2，此时A、B 相绕组都保持状态1，来减小输出转矩。随着B 相转矩的增加，使转矩误差小于0，此时需要减小输出转矩。但由于B 相即将进入单相导通，则B 相进入续流状态0 来停止转矩减小，而A相进入状态－1 进行退磁磁。以下是分别在单相导通区和换相导通区滞环设计图［7］。

3 SRM 模糊PI 速度控制器的设计

模糊控制是将输入量按一定的模糊控制规则自动进行推理运算，比较适宜处理不确定性和不精确性问题，因而具有响应速度快、鲁棒性好等特性。而模糊PI 复合控制是在模糊控制的基础上引入了积分的环节，其结构图如图5 所示，当系统误差较大时采用模糊控制器，当系统误差小于一定的值，切换到PI 控制器，让PI 控制器完成系统响应后期的控制工作。这样可以配合工作保证系统的稳定性，从而改善系统的静态性能［8］。

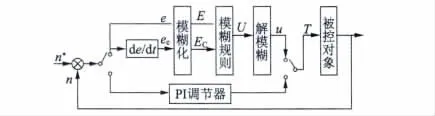
图5 模糊PI 复合控制结构框图

3.1 确定模糊控制的量化因子及隶属函数

本文电机稳定运行在1 000 r/min，因此取速度误差与速度误差变化率的基本论域［－1 000，1 000］，取参考转矩的基本论域为［－200，200］。由于电机转速差范围较大，为了进一步提高电机调速性能，将偏差变量E、偏差变化率EC及控制量U 的论域均为{－6，－5，－4，－3，－2，－1，0，1，2，3，4，5，6}，其模糊集反模糊化公式为［9］

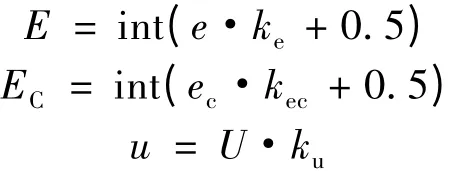
式中:ke= 6 /1 000，kec= 6 /1 000，ku= 200 /6，取隶属度函数为三角形函数，语言变量的模糊子集为 “负大，负中，负小，零，正小，正中，正大”即{NB，NM，NS，ZE，PS，PM，PB}。

3.2 模糊控制规则与模糊推理

模糊控制规则是基于操作者的经验和相关专家的知识得出的，本文根据电机控制经验和大量的模拟仿真，得到了模糊控制规则集，如表l 所示。

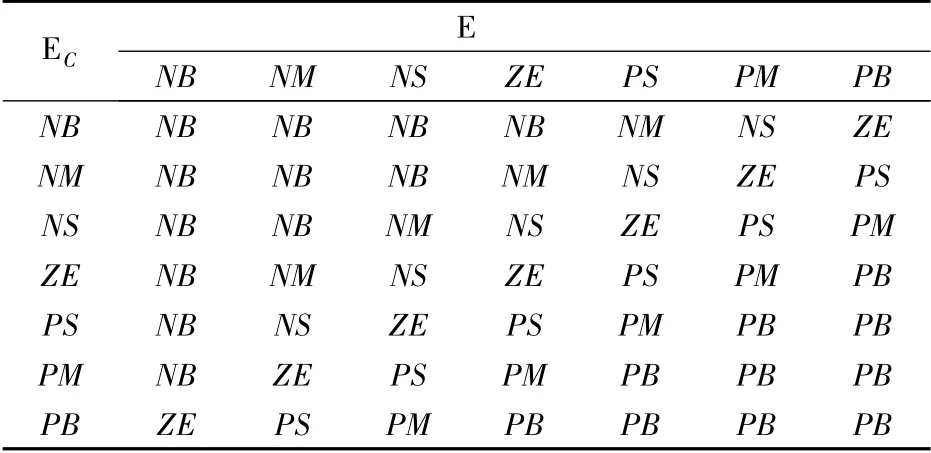
表1 模糊控制量U

模糊推理系统采用Mamdani 类型，即采用如下形式的模糊蕴含关系:If AiAnd Bj，then Cij(其中Ai，Bj，Cij分别表示E，EC和U 的对应语言值)。

4 DITC 系统仿真结果及分析

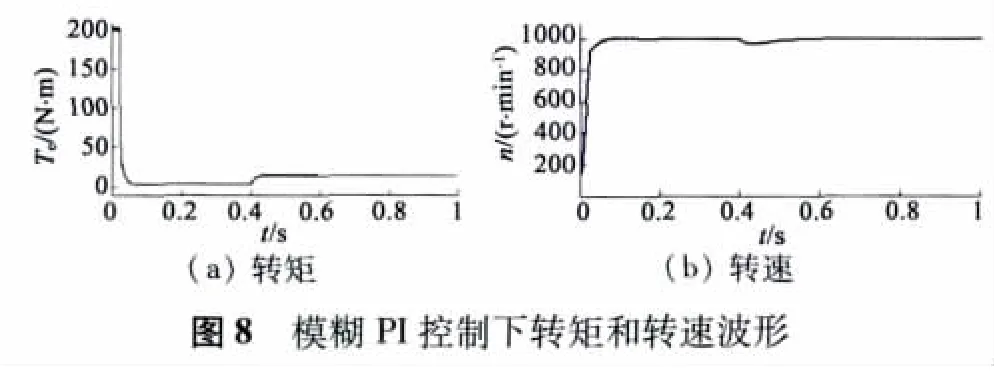
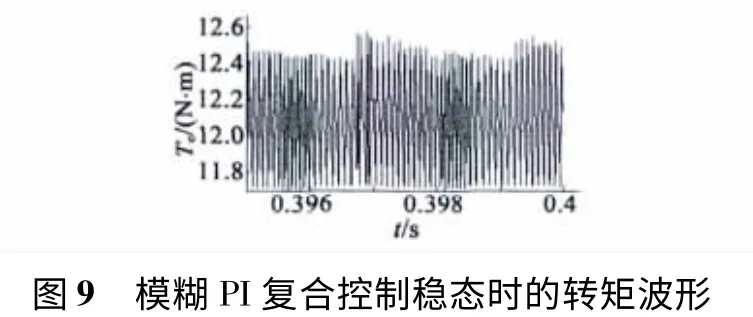
四相8/6 结构的SRM 的DITC 系统中，导通角设为23°。其中开通角设为32°，关断角设为55°。给定转速1 000 r/min，0．4 s 后加入负载转矩10 N·m，要求电机速度能稳定运行1 000 r/min。图6、图7 是模糊控制和PI 控制下的转矩和转速波形，图8、图9是模糊PI 控制和模糊PI 复合控制下的转矩波形。

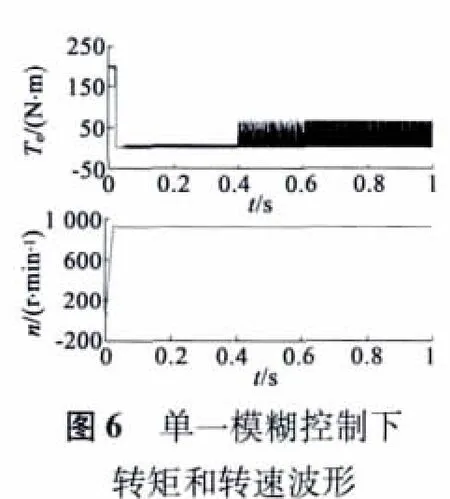
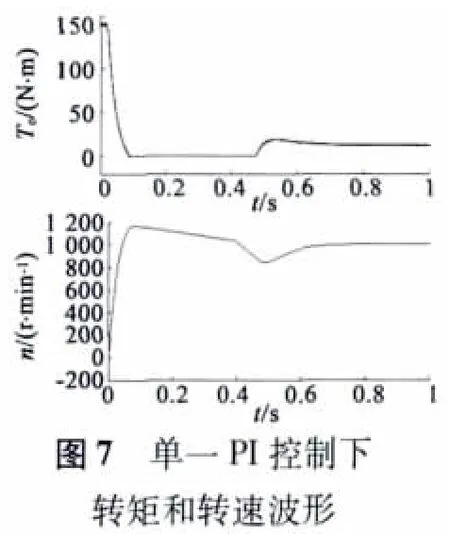
对比图6、图7 分析可知，单一模糊控制存在稳态静差，而复合控制稳态无静差。

对比图7、图8 分析可知，在0．4 s 突加负载后模糊PI 复合控制器具有较好的抗干扰能力，鲁棒性好，而且超调较小。

系统稳态输出转矩如图9 所示。通过计算可知，转矩值在11．7～12．6 N·m 之间波动，其转矩脉动仅为6．67%，有效减小了SRM 转矩脉动。

因此模糊PI 控制解决了常规PI 控制器超调量与调节时间的矛盾，同时也解决了单一模糊控制器存在静差的问题。而且模糊PI 控制使得系统稳态无静差，系统抗扰性能优越，而且超调小，动静态性能都优于单一模糊调节器。

5 结 语

本文应用了直接瞬时转矩控制的方法对SRM进行控制，而且验证了DITC 方法能够在一定导通角内能有效改善SRM 的动静态转矩性能，减小转矩脉动。并且本文采用了模糊PI 复合控制，把两种控制器结合起来，发挥各自优点，取得了较为满意的结果。仿真结果表明该复合控制器具有良好的动静态性能，鲁棒性好。

［1］ 刘迪吉．开关磁阻电机发展及应用［J］．电气技术，2006(07):22 －25．

［2］ 夏长亮，陈自然，李斌．基于RBF 神经网络的开关磁阻电机瞬时转矩控制［J］．中国电机工程学报，2006，26(19):127－132．

［3］ 丛望，米芳芳．基于模糊PID 控制的开关磁阻电动机调速系统的建模和仿真［I］．船电技术，2008，28(1):39－42．

［4］ Inderka R B，De Doncker R W．DITC－direct instantaneous torque control of switched reluctance drives［J］．IEEE Transactions Industry Applications，2002，39(4):1046－1051．

［5］ 漆汉宏，张婷婷，李珍国，等．基于DITC 的开关磁阻电机转矩脉动最小化研究［J］．电工技术学报，2007(7):136－140．

［6］ 漆汉宏，张婷婷，李珍国．基于DITC 的开关磁阻电机转矩脉动抑制仿真研究［J］．系统与仿真学报，2009(10):3133－3138．

［7］ 程勇，林辉．直接瞬时转矩控制策略在开关磁阻电机上的应用［J］．航空制造技术，2012(10):88－91．

［8］ 王勉华，梁媛媛．开关磁阻电机直接转矩模糊PI 控制器设计［J］．电气传动，2010，40(1):51－54．

［9］ 张振国，徐建科，江涛，等．开关磁阻电机直接转矩模糊控制器设计与仿真［J］．计算机仿真，2012(9):178－181．