基于模糊PI 的超声波电动机频率追踪控制

张 帆，罗辞勇

(重庆大学输配电装备及系统安全与新技术国家重点实验室，重庆400044)

0 引 言

超声波电动机是20 世纪80 年代发展起来的一种利用压电材料逆压电效应的新型微特电机，相比传统的电磁电动机有快速响应、断电自锁、无电磁干扰、重量轻、结构紧凑等优点。但由于超声波电动机独特结构和运动机理，其开环输出特性会随着环境温度、摩擦损耗、预压力、驱动器激励频率等因素的变化而变化［1］。

超声波电动机的控制方法主要有调压控制、调频控制和调相控制三种。按控制策略的不同可以分为固定增益的PI 控制、变增益的PI 控制、自适应控制、神经元控制和模糊控制等［1－2］。本文在TRUM－60 的基础之上以调频控制为方法实现了超声波电动机的自动追频控制，为超声波电动机中的模糊PI 控制设计提供借鉴。

1 超声波电动机的控制系统

图1 是超声波电动机模糊PI 控制的系统框图，其特点如下:

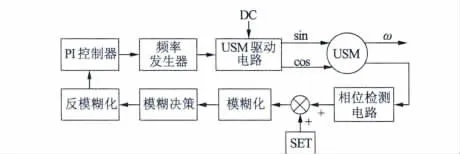
图1 超声波电动机模糊PI 控制系统框图

(1)频率发生器控制着USM 驱动电路中输出的驱动信号频率。

(2)USM 驱动电路将低压直流电源放大并提供匹配电路实现超声波电动机驱动信号高压高频的要求，能实现正反转控制。

(3)相位检测电路实现对超声波电动机运行时的相位检测。

(4)相位误差通过模糊计算对PI 控制器进行输出控制以实现PI 参数的变增益控制，最后PI 控制器的输出实现对频率的自动跟踪。

模糊控制的优点是不依赖于控制对象精确的数学模型，根据人工控制规则组织控制决策表，具有一定的灵活性、适应性和鲁棒性等［1～3］，缺点是对经验的依赖性较强。

1.1 PI 控制的基本原理

由于积分作用的存在，正弦信号经过PI 控制器后会发生四分之一个周期的延迟，所以PI 控制器构成的是滞后校正。PI 控制器可以保证系统的稳定精度，但却是以对快速性的限制来换取系统的稳定。

比例参数KP的作用是加快系统的响应速度，提高系统的调节精度。随着KP的增大，系统的响应速度越快，调节精度越高，但容易产生超调使系统的稳定性变差，甚至不稳定。KP过小，调节精度低，响应速度慢，系统的动静态性能变坏。

积分作用参数Ki的主要作用是消除静态误差，并且值越大，系统的稳态误差消除得越快，但Ki也不能过大，否则在响应过程的初期会产生积分饱和现象。若过小，系统的稳态误差将难以消除，影响系统的调节精度。

1.2 模糊控制的基本原理

模糊控制是一种基于自然语言控制规则、模糊逻辑推理的计算机控制技术，它不依赖于控制系统的数学模型，而是从模糊理论给出的有效方法，将语言表达的知识或规则根据操作经验、表述知识转换成“模糊规则”的智能控制。

模糊控制器通常包括模糊化、模糊决策、清晰化处理等环节，根据模糊规则推理类型的差异，模糊控制器主要可以分为Mamdani 型和T－S 型两种控制器，图2 为模糊控制器设计的主要流程图［3－4］。

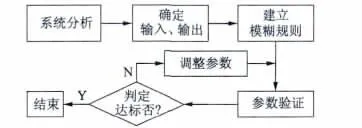
图2 模糊控制器的设计

1.3 模糊PI 控制

模糊控制和PI 控制相结合的方式目前主要有三种:

分段控制是在误差较大的时候采用模糊控制，而在误差进入到一定范围时通过切换开关转换到传统的PI 控制。

并联混合是通过模糊控制和PI 控制并联而成的混合型模糊PI 控制器

在线整定PI 控制的参数是利用模糊控制器在线整定PI 控制器参数的自适应模糊PI 控制器。

PI 控制分为固定增益的PI 控制和变增益的PI控制。固定增益的PI 控制算法简单，控制器调整方便，但相对于变增益的PI 控制其控制的性能指标如超调量、控制周期、抗干扰能力等都不如后者。本文所采用的模糊PI 控制是一种变增益的PI 控制，以确定的误差作为输入量根据设定的模糊规则，当输入在不同的值域时有不同的PI 参数与之对应，有着良好的控制性能指标。

2 模糊PI 在超声波电动机控制中的设计方法

2.1 输入信号

本文模糊PI 控制器以实现超声波电动机的自动追频为目的，找到超声波电动机正常工作时的谐振点，以超声波电动机电流和电压的相位差为控制器的输入。

相位差定义:

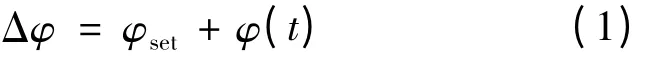
式中:φset为相位的设定值，考虑到超声波电动机的非线性因素［1－2，6－7］，在设定相位的时候需要考虑温度给频率带来的漂移;φ(t)为实时采样超声波电动机的相位输入信号。

2.2 比例变换

为了使变量按一定的比例进行方法或缩小从而对清晰值进行比例变换，模糊控制设有量化因子模块和比例因子模块。

输入到模糊控制器的向量Δφ 是一个清晰值，经过模糊化(D/F)转换，变成模糊量之后才能输入到模糊推理模块进行推理，把清晰值从物理论域映射到模糊论域N 上的变换系数就叫做量化因子。

而从模糊论域转换到物理论域的转换系数称为比例因子。

2.3 Mamdani 模型

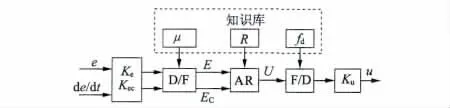
图3 Mamdani 二维模糊控制器原理图

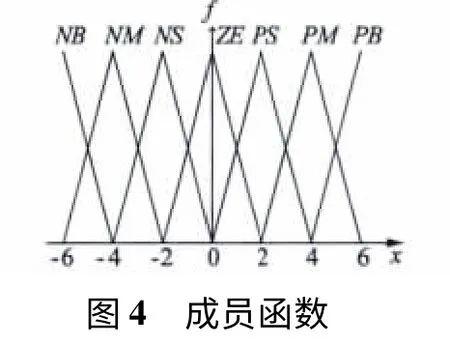
本文选择的成员函数为三角形分布函数，如图4 所示。

3 仿真分析

在上述理论分析的基础上进行了仿真分析与讨论，实验采用超声波电动机的等效电路模型，首先通过推挽电路将12 V 的直流电源进行放大，然后通过交－直－交整流逆变电路对输出电压的幅值和频率进行控制，以达到驱动超声波电动机的要求。

实验以自动追频为目的，通过对超声波电动机电流电压的相位检测来计算相位差e，将这个e 送入到控制器中，然后通过控制器的输出对交－直－交整流逆变电路频率进行控制。由于模糊控制是建立在一定的经验基础之上，所以在进行模糊PI 控制之前需要做固定增益的PI 控制实验。

图5、图6 分别为固定增益PI 控制的超声波电动机相位检测波形和PI 输出波形。从图中可见，PI控制的稳定时间约为60 ms，超调量δ 为30% 左右。

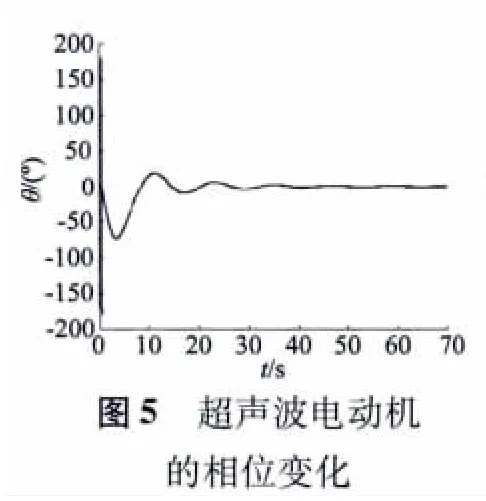
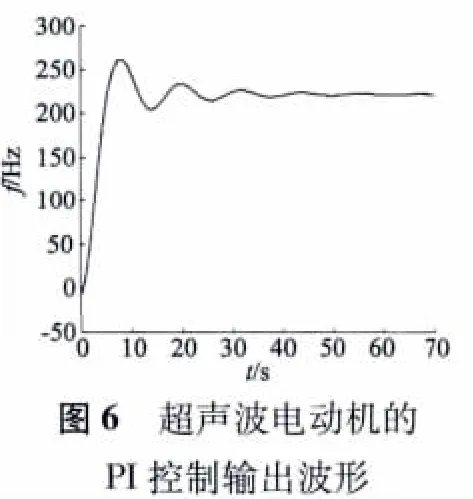
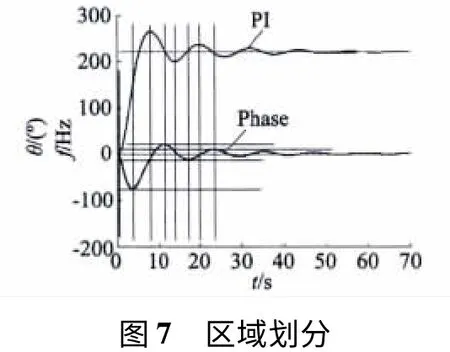
通过固定增益PI 控制的超声波电动机相位检测波形和PI 输出波形的对比，可以累计一定的经验来指导模糊控制。根据超调量和控制周期的指标要求，可以将图6 做以下所示的区间划分，如图7 所示。

从实验可以得到，检测到超声波电动机相位差的变化区间为(－75．9°，21．78°)，对此数据进行修正后相位变化的区间变为(－77°，21°)。将量化因子的值取为7，相位变化的区间可以分为14 个部分，又根据固定增益PI 的输出波形，将相位变化的区间进一步划分为4个部分，即(－77°，－14°)、(－14°，0)、(0，7°)和(7°，21°)。并且由于相位在瞬时是波动变化的，所以这里的模糊PI 控制不适合根据相位变化率来设置模糊规则，因此得到第一种情况下的“IF－THEN”模糊控制决策，具体模糊数的设置如表1 和表2 所示。

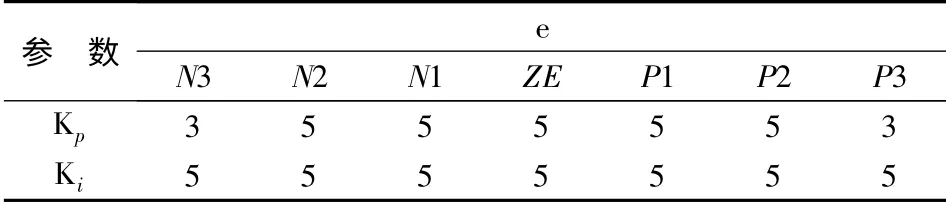
表1 模糊决策1 的模糊数1

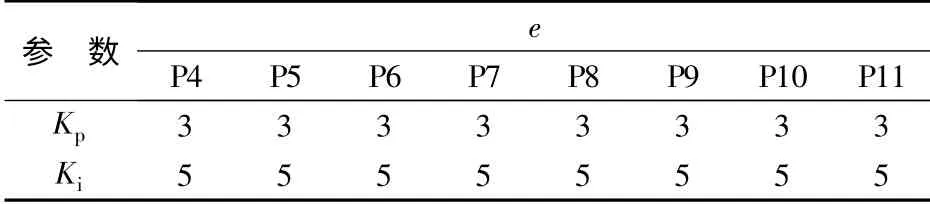
表2 模糊决策1 的模糊数2

图8、图9 分别为在模糊控制决策1 下的相位检测波形和模糊PI 控制器的输出波形。经过计算得到当超声波电动机发生串联谐振时控制器的输出应该为220．1 Hz，所以图9 中超调量δ 在52．74% 左右，稳定控制时间t 约为25 ms。在模糊决策1 下的模糊PI 控制器在超调量上和固定增益的PI 控制器相当，但在达到稳定的时间上优势比较明显，由此体现出了模糊PI 相对于固定增益PI 控制的优势。

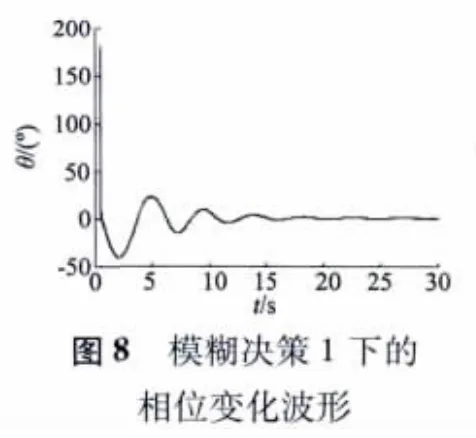
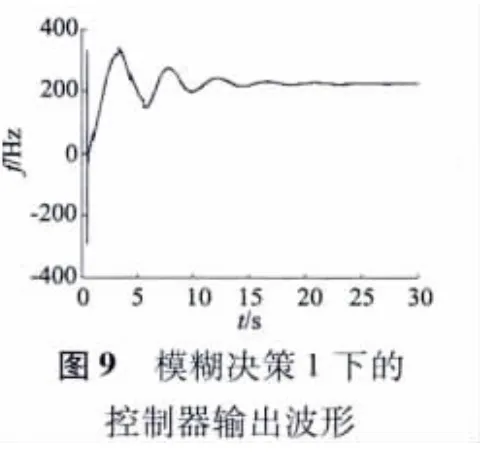
表3 和表4 是在PI 控制的基础上根据模糊决策1 改进后的模糊决策2，Kp的模糊数没有变化，而对Ki的模糊数进行了改变;当e 较小时取较大的Ki;当e 处于中等大小时适中的Ki;当e 较大时可以选择去掉积分作用。

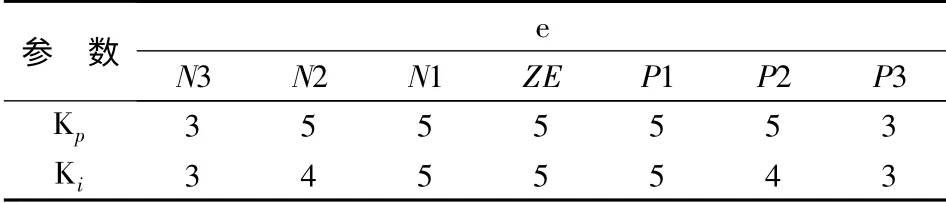
表3 模糊决策2 的模糊数1

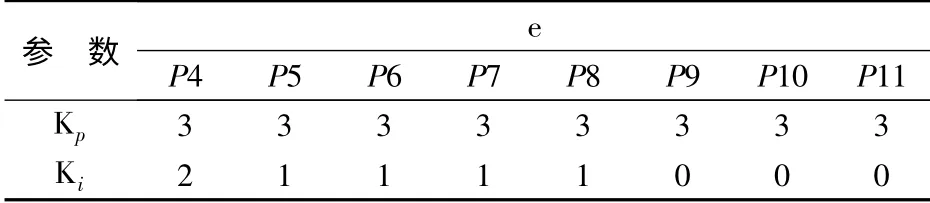
表4 模糊决策2 的模糊数2

图10、图11 分别为在模糊决策2 下的相位检测波形和模糊PI 控制器的输出波形。图11 中输出波形的最大值为280 Hz，超调量δ 在27．2% 左右，稳定控制时间t 在22 ms 左右。

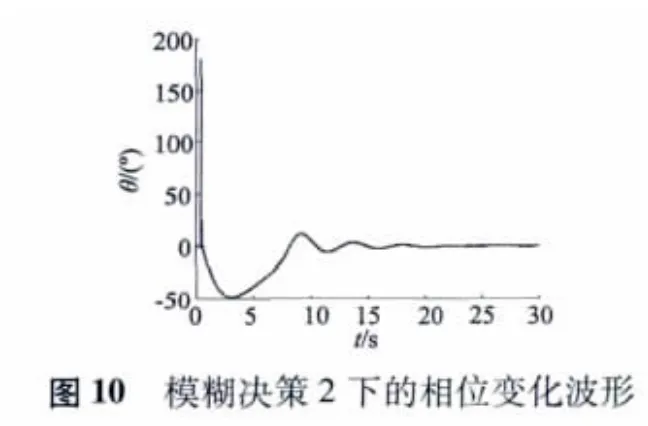
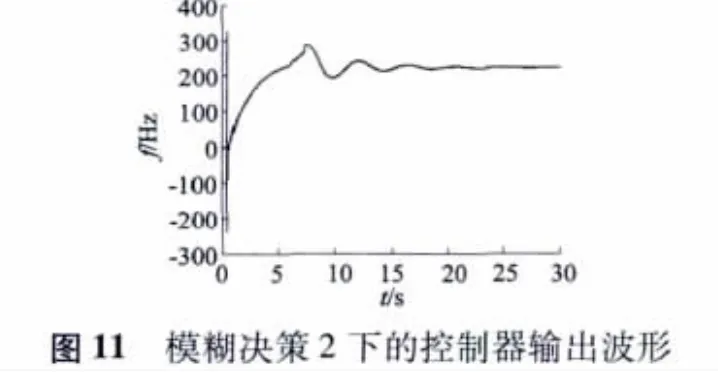
从图11 中可以看到，在模糊决策2 下的控制波形相当于模糊决策1 在超调量这一性能指标上有比较明显的优化。

根据模糊决策1 和2 的控制效果，希望对模糊决策进行改进，以期望在超调量δ 和控制时间t 上获得更好的控制效果。

表5 和表6 是在PI 控制的基础之上根据模糊决策2 改进后的模糊决策3，Ki的规则没有变化，在对Kp进行模糊规则进行了改变:当e 较小时取较大的Kp;当e 处于中等大小时取较小的Kp;当e 较大时取较大的Kp。

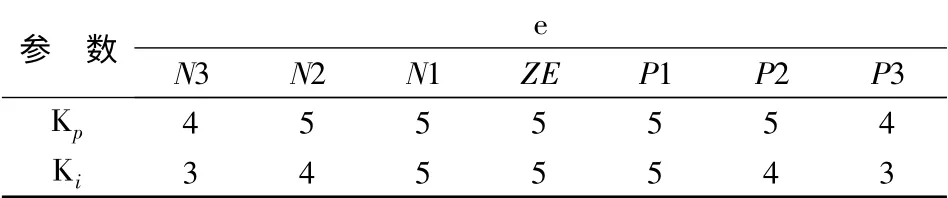
表5 模糊决策3 的模糊数1

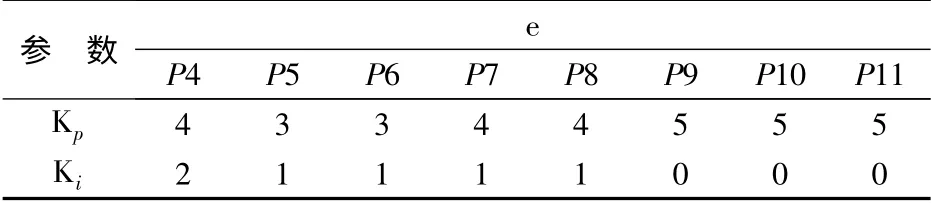
表6 模糊决策3 的模糊数2

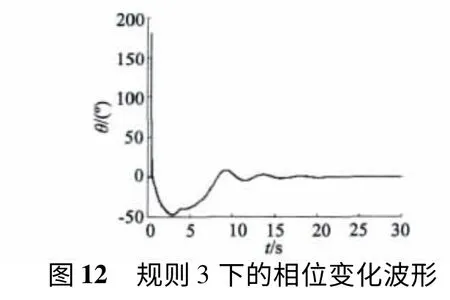
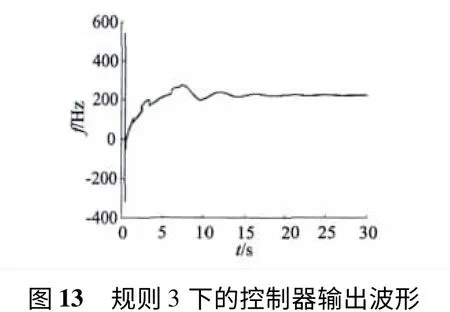
图12、图13 分别为模糊控制决策3 下的相位检测波形和模糊PI 控制器的输出波形。图13 中模糊PI 控制器的输出最大值为272．4 Hz，超调量δ 约为23．7%，系统到达稳定时间t 约为19 ms，因此模糊决策3 的控制效果优于模糊决策2 并且明显好于固定增益的PI 控制。

最后，总结模糊PI 控制器的模糊规则的设定规律:当e 较大时，Kp的模糊数较大，但不得过大，以防止系统进入不稳定状态，可去掉积分作用，令Ki的模糊数为0;当e 处于中等大小时，Kp的模糊数取较小，以减小系统的超调量，较小的Ki模糊数;当e较小时，为了使系统具有较好的稳定性，Kp和Ki的模糊数都应取较大值。

4 结 语

在未获得超声波电动机精确数学模型的情况下，本文采用了基于固定增益经验基础之上的模糊PI 控制策略，从超调量δ 和到达稳定的时间t 两方面来衡量都取得了很好的效果，系统具有较高的控制精度和较好的稳定性，并总结出了模糊PI 控制器中模糊规则的规律，为超声波电动机模糊PI 控制提供一定的借鉴。

［1］ 赵淳生．超声电机技术与应用［M］．北京:科学出版社，2007．

［2］ 胡敏强，金龙，顾菊平．超声波电机原理与设计［M］．北京:科学出版社，2005．

［3］ 夏长亮，徐绍辉，史婷娜，王娟，陈炜．基于遗传算法的超声波电机模糊自适应速度控制［J］．中国电机工程学报，2003，23(3):99－103．

［4］ 石辛民，郝整清．模糊控制及其MATLAB 仿真［M］．北京:清华大学出版社，2008．

［5］ 周华伟，温旭辉，赵峰，张剑．一种具有预测功能的抗积分饱和的PI 速度控制器［J］．电机与控制学报，2012，16(3):15－21．

［6］ 曾劲松，姚志远，赵淳生．超声电机中的非线性现象研究［J］．中国机械工程，2006，17(10):1047－1051．

［7］ 王光庆，郭吉丰．超声波电机频率－温度特性研究［J］．电机与控制学报，2008，12(6):675－679．

［8］ 牛洪海，赵荣祥，吴茂刚．基于模糊PI 参数自整定的永磁同步电机矢量控制系统［J］．电气应用，2005，24(12):79－82．

［9］ 李华峰，王红占，黄卫清．控制量独立可调的超声电机新型驱动器［J］．电机与控制学报，2010，14(9):88－92．