新型Anti－W indup PI 控制器在感应电机DTC 系统中的应用

苗敬利，李启蒙

(河北工程大学，河北邯郸056038)

0 引 言

直接转矩控制(以下简称DTC)技术［1－4］是一种高性能的现代交流调速技术，它的出现稍晚于矢量控制技术。但相比于矢量控制，DTC 技术控制量明确、控制手段直接、控制方法简单，而且，直接转矩控制内部没有电流环，可以不受电流调节器带宽的限制，因此相对于矢量控制，转矩动态响应快，对电机参数的变化不敏感，鲁棒性强。但是典型的感应电机DTC 系统的转速控制器一般都采用PI 控制器，控制器的输入为给定转速和实际转速的差值，输出为转矩的给定值。由此可见，转速控制器的性能在很大程度上影响着DTC 系统的控制性能。

实际的感应电机调速系统，受到实际硬件设备的限制，电机的实际转矩是有上限值的，不能无限制增大。而常规PI 控制器并不考虑实际转矩的上限值限定，当转速发生突变时，PI 调节器会输出一个很大的转矩，但实际的电机是无法输出这么大的一个转矩的，此时电机只能输出本身所能输出的最大转矩，这种现象就叫做积分饱和现象(Windup)。Windup 现象的出现会使得系统的闭环响应变差，例如:系统的超调量将变大、调节时间会变长，甚至会造成系统的不稳定［5－7］。

为抑制积分饱和现象，人们提出了一些抗积分饱和(Anti－Windup)方案，主要有条件积分法和反计算法。反计算法设计容易，目前在工程上常采用。但反计算法的瞬时控制性能非常依赖于反馈增益系数而不是PI 控制器的参数，而在实际应用中定量设计控制系统的性能指标是难以实现的［8］。

针对以上问题，本文为感应电机DTC 系统引入了一种新型Anti－Windup 控制器，这种控制器在PI控制器出现饱和时，可以快速地退出饱和区，从而实现了减小超调量，加快响应速度的目的。

1 新型Anti－W indup PI 控制器

在感应电机中转速和转矩的关系可由式(1)的一阶线性系统表示:

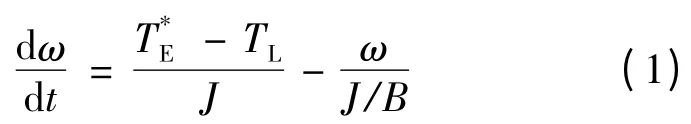
用s 函数可表示为:

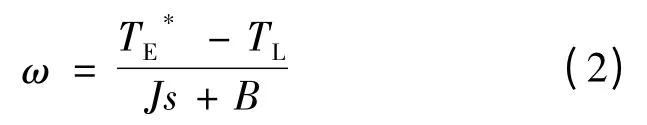
式中:ω 为转子的机械角速度;J 为电动机的转动惯量;B 为粘滞摩擦系数;T*E是电机的给定转矩;TL为负载转矩;J /B 被称为机械时间常数。

传统的PI 控制器由于其受到Windup 现象的影响，相当于在输出端加入了一个限幅函数T*E(u)，式(3)是其表达式，图1 是其所对应的函数曲线。图2 为带饱和限幅的PI 控制器结构图。

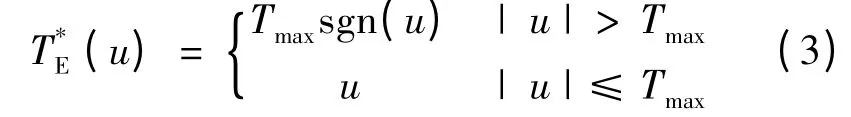
式中:u 为PI 控制器的输出，sgn(u)为符号函数。

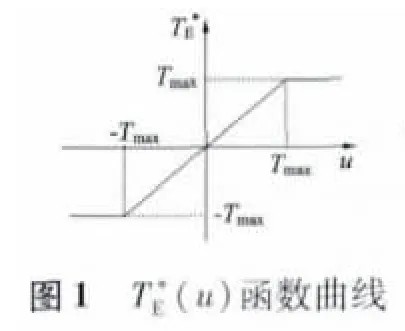
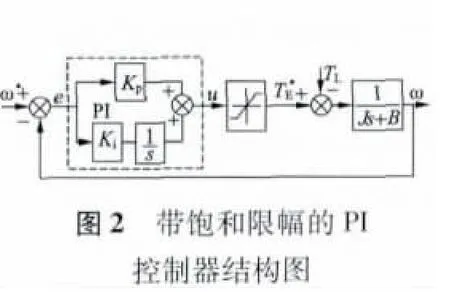
为了很好地抑制饱和现象，本文为感应电机DTC 系统引入了一种新型Anti－Windup PI 控制器，图3 给出了其控制框图。这种控制器的工作原理:先判断控制器的饱和状态，然后再根据是否饱和对积分状态i 进行两种不同的控制，当不饱和时(u =T*E)，开关S1闭合，S2打开，此时控制器为典型的PI控制器;当饱和时(u ＞T*E)，S1断开，S2闭合，把反馈的输出乘以某一负系数(－1 /k)后反馈到其输出，这样可以使积分输出快速的收敛为零。

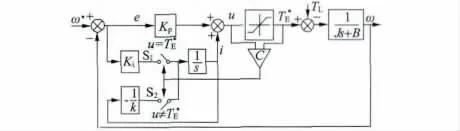
图3 新型Anti－Windup PI 控制器结构图

由图3 所示，积分状态i 的表达式:

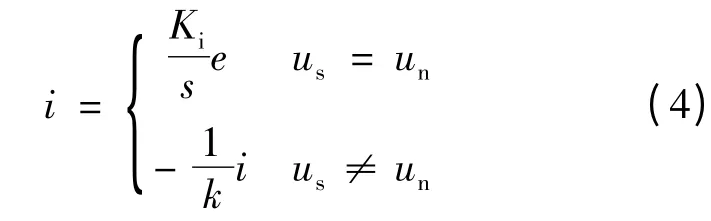
式中:Ki为积分常数;k 为积分反馈增益系数;若设km= J/B，即km为机械时间常数，那么满足k，Ki≪km。

2 新型Anti－W indup PI 控制器稳定性分析

要想系统能够稳定，则必须满足两个条件:第一系统在线性区内是趋向稳定的;第二系统能够由饱和区收敛到线性区。若两个条件同时满足，可保证系统最终趋向稳定。

2.1 在线性区渐近稳定的条件

在线性区时，新型抗饱和PI 控制器相当于是一个常规的PI 控制器，此时误差方程可写为:

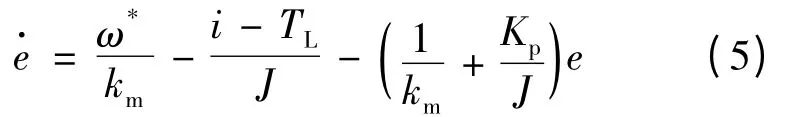
定义如下李雅普诺夫函数:

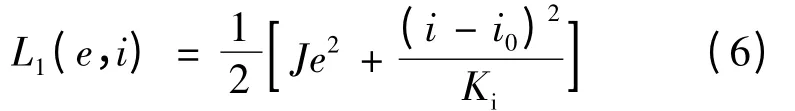
式中:i0是i 的稳态值，所以有:

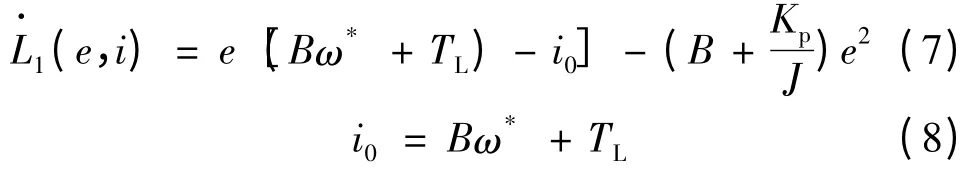
而在线性区总满足:

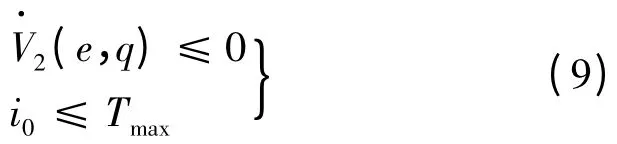
由此可以得控制器在线性区渐近稳定的条件:

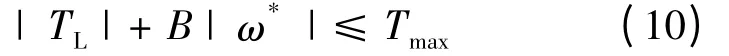
2.2 系统由饱和区收敛到线性区的条件

由式(1)可知，对于给定的阶跃响应参考转速，转速误差方程:

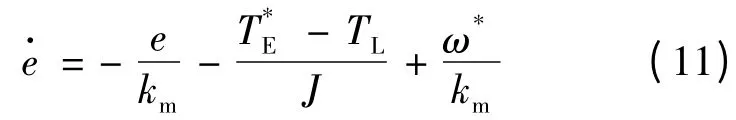
在饱和区时由式(4)可知，积分状态i 满足如下动态方程:

由式(4)可以看出，积分状态迅速收敛到零，而k≪km，即转速误差的动态远远慢于积分状态的动态，也就是说，积分状态i 在控制器处于饱和状态时立刻被置为零。由此可得:

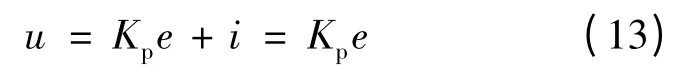
设Eb= Tmax/Kp，从式(13)可看出，当| e | ≤Eb时，控制器在线性区运行，| e | ＞Eb时控制器在饱和区运行。

定义如下的李雅普诺夫函数:

求导有:

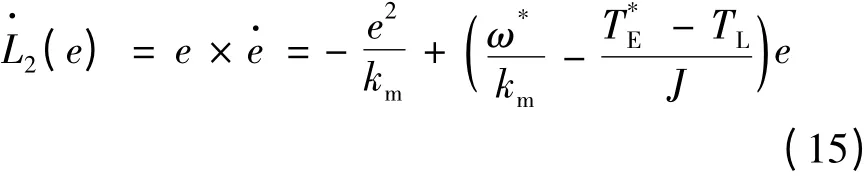
把式(2)和式(13)代入式(15)，得

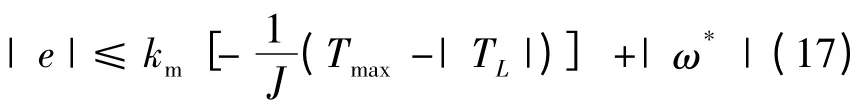
当| e | ＞Eb时系统能够由饱和区进入线性区，所以控制器能从饱和区到达线性区的吸引条件:

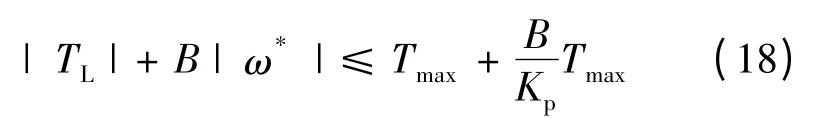
比较式(10)和式(18)可以看出，只要满足式(10)必然满足式(18)，所以式(10)是新型Anti －Windup PI 控制器能够趋向于稳定的条件，即:

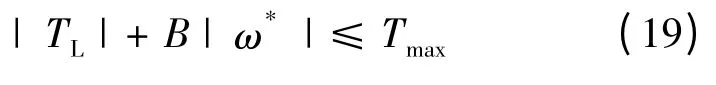
3 建模与仿真

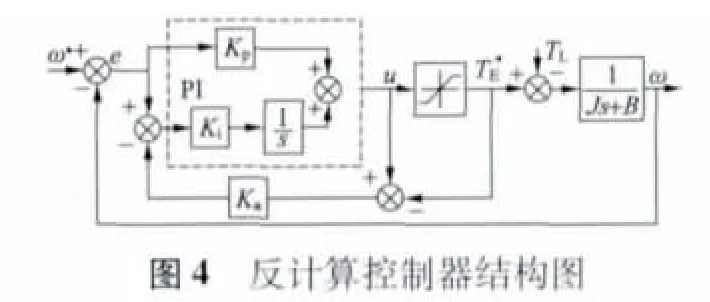
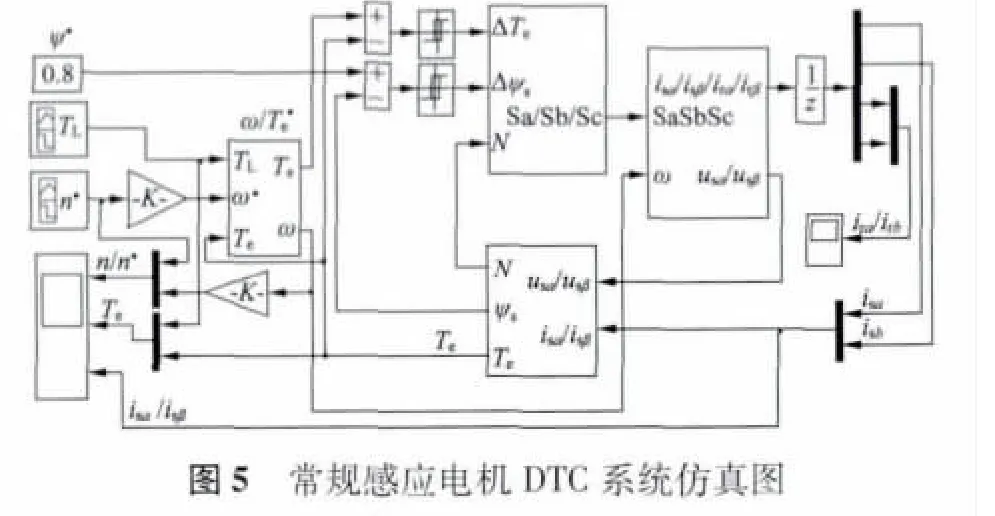
为了对新型Anti－Windup PI 控制器的性能进行参考比较，现给出了反计算控制器的结构图，图4所示。应用MATLAB /Simulink 进行建模仿真，如建立常规PI 控制器的感应电机DTC 系统的模型，如图5 所示。然后再分别建立反计算法控制器模型和新型Anti－Windup PI 控制器模型，如图6 和图7 所示。再用反计算控制器和新型Anti－Windup PI 控制器代替传统PI 控制器，得到不同的转速响应的仿真波形。

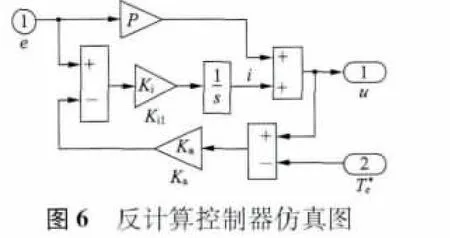
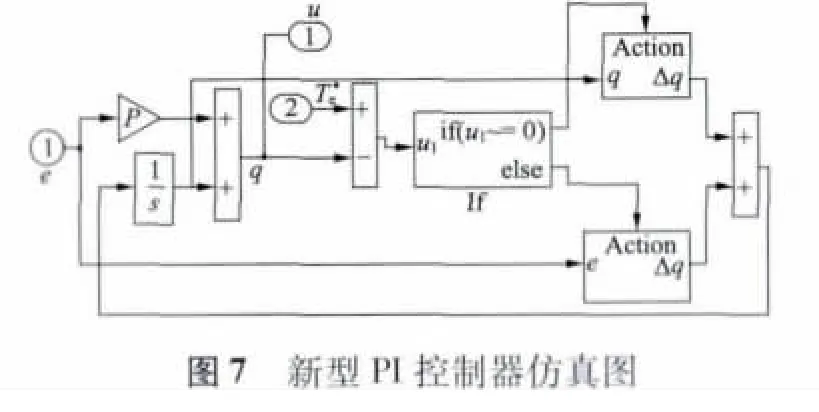
4 仿真结果

电机参数如下:定子电阻Rs= 2．5 Ω，转子电阻Rs= 2．7 Ω;定子电感Ls= 0．332 5 mH，转子电感Lr= Ls= 0．332 5 mH，互感Lm= 0．319 4 mH;电机极对数P = 2，转动惯量J = 0．008 6 kg·m2;三个控制器中的PI 参数都为Kp= 1，Ki= 10;反计算控制器中的Ka= 1，新型Anti－Windup PI 控制器中的k = 0．95;电机最大输出转矩Tmax= 10 N·m;离散采样周期50 μs;定子磁链给定值ψ*= 0．8 Wb。

感应电机空载起动，转速在0．1 s 时由0 阶跃为400 rad /s。为研究各控制器的抗负载扰动能力，在1 s 时加入4 N·m 的负载转矩。

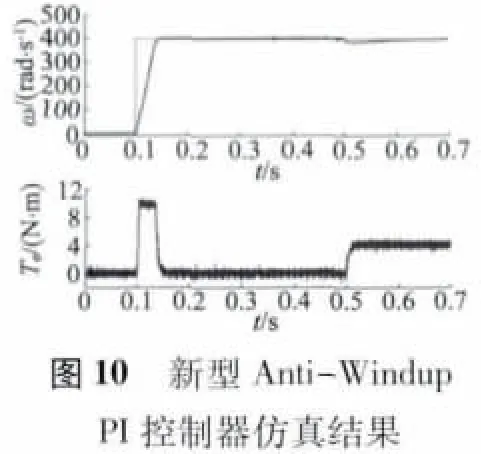
仿真后得到如图8～图10 所示的仿真曲线，图11 是三种控制器的仿真结果，从中可以看出，转速阶跃响应的超调量和响应时间都不同，而转矩曲线几乎一致。图12 和图13 分别是图11 的局部放大图。

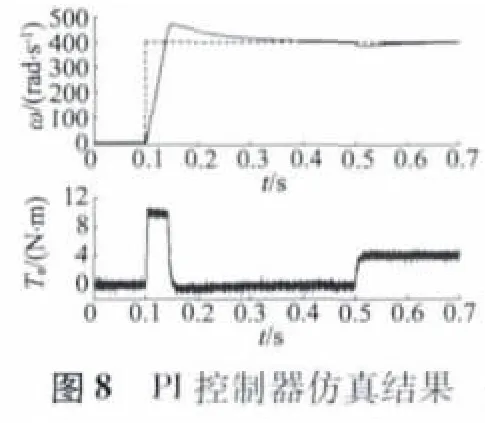
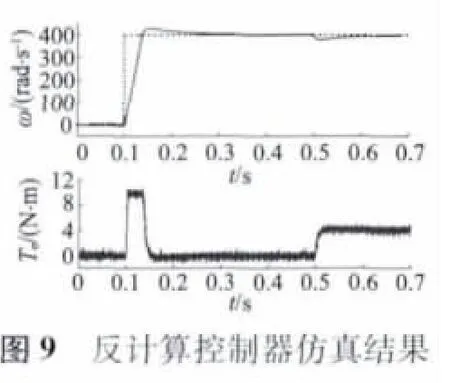
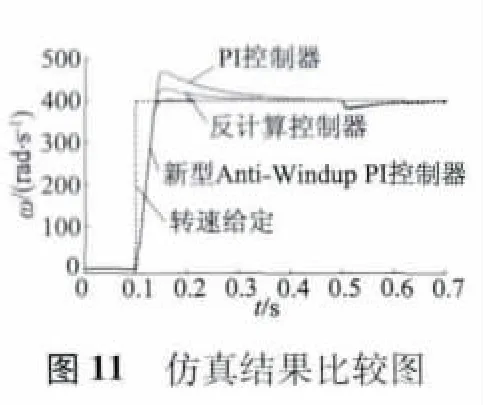
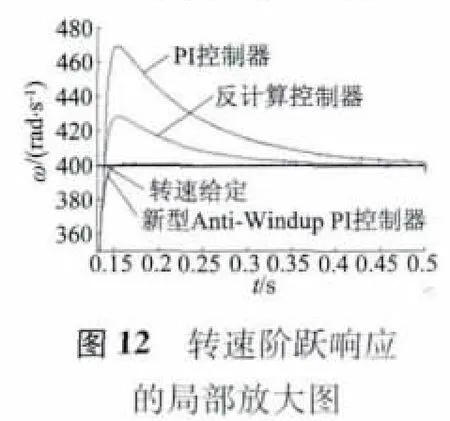
从图12 的局部放大图可以看出，当0．1 s 转速由0 阶跃为400 rad /s 时，常规PI 控制器的转速响应的超调量达到了17．5%，调节时间为0．6 s;反计算控制器的超调量为7．5%，调节时间为0．45 s;新型Anti－Windup PI 控制器几乎没有超调，而且调节时间仅有0．25 s。由仿真结果可以看出，新型Anti－Windup PI 控制器的控制性能有很明显的优势。

当加入4 N·m 的负载时，由图10 的局部放大图可以看出，三条曲线很接近，常规PI 控制器和新型Anti－Windup PI 控制器的对应曲线几乎重合，只有反计算控制器的对应曲线的波动稍微大一点，所以常规PI 控制器和新型Anti－Windup PI 控制器的抗负载扰动能力比反计算控制器稍好，但差别不大。

5 结 语

由于常规感应电机DTC 系统的转速PI 控制器存在着积分饱和的问题，所以本文采用了一种新型Anti－Windup PI 控制器，并给出了系统稳定收敛的条件，最后用MATLAB 对系统进行了建模和仿真，仿真结果表明，新型Anti－Windup PI 控制器能够减小甚至消除转速响应的超调量，并且缩短了调节时间。同时该控制器还具有结构简单和易于工程实现的优点。

［1］ Takahashi I，Naguchi T．A New Quick－response and Hing－efficiency Control Strategy of an Induction Motor［J］．IEEE Transaction on Induction Applications(S0093－9994)，1986，22(5):820－827．

［2］ 陈伯时，陈敏逊．交流调速系统［M］．北京:机械工业出版社，2006．

［3］ Trzynadlowski A M．异步电机的控制［M］．李鹤轩译．北京:机械工业出版社，2003．

［4］ 薛定宇，陈阳泉．基于Matlab/Simulink 的系统仿真技术与应用［M］．北京:清华大学出版社，2002．

［5］ 王焕钢，徐文立，黎坚，等．一种新型的感应电动机直接转矩控制［J］，中国电机工程学报，2004，24(1):108－111．

［6］ 杨明，徐殿国，贵献国．控制系统的Anti－Windup 设计综述［J］，电机与控制学报，2006，10(6):622－626．

［7］ 周华伟，温旭辉，赵峰，等．一种具有预测功能的抗积分饱和PI 速度控制器［J］，电机与控制学报，2012，16(3):15－21．

［8］ 于艳君，柴凤，高宏伟，等．基于Anti－Windup 控制器的永磁同步电机控制系统设计［J］，电工技术学报，2009，24(4):66 －70．