考虑柔性模态的硬盘音圈电机快速精确定位控制

刘 磊，赵艳彬，王本利

(1．大连理工大学，辽宁大连116024;2．上海卫星工程研究所，上海200240;3．哈尔滨工业大学，黑龙江哈尔滨150080)

0 引 言

硬盘尺寸越来越小，但是容量越来越大，需要磁头进行快速精确定向，提高硬盘读取速度和精度［1］。在硬盘读取速度要求不是很高时，音圈电机的模型可以采用双积分，但是当需要更快的闭环带宽时，高频动力学模态可能被控制器激发，简单的PID 控制器或其他基于音圈电机刚体模型的控制器可能会发生溢出，使系统失去稳定性。于是提出了许多复杂的非线性控制，Venkataramanan 考虑音圈电机一阶柔性模态并设计了模态切换控制［2］，Wua S 设计了迭代学习控制器［3］。

本文设计了超前滞后补偿、PD 及陷波滤波器联合控制音圈电机，镇定时间小于0．001 s，超调5%，可以同时满足了快速跟踪和精确定位的指标，并且执行简单。

1 滞后超前及PD，陷波滤波联合控制

音圈电机的动力学模型可以分为刚体部分和柔性模态部分［2］。即:

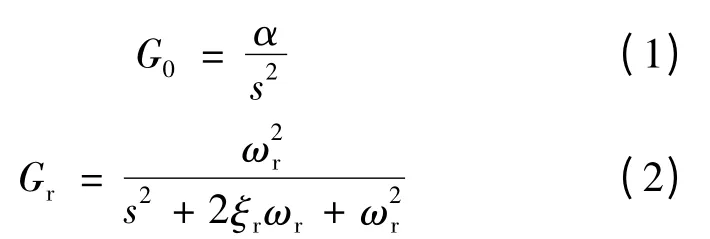
式中:Gr只考虑了一阶模态。音圈电机模型可以写成:

设计指标要求音圈电机对节约信号的镇定时间小于0．001 s，并且超调小于10%。

根据二阶系统理论［4］，超调和阻尼的关系如下:

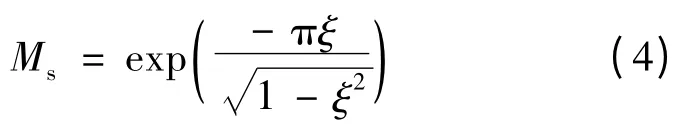
式中:Ms＜10%，阻尼比ξ ＞0．6。

先考虑简单的PD 控制［4］，为了达到设计的镇定时间，满足带宽的要求，取比例系数1，微分系数0．000 04，系统的影响如图1 所示，从图1 中可以看出，音圈电机的柔性模态被激发，控制器发生溢出，闭环系统失去稳定性。

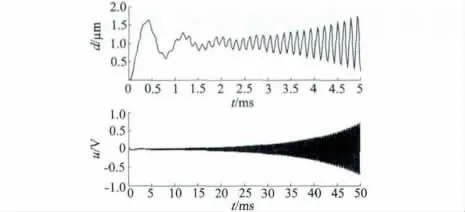
图1 PD 控制性能

为保证系统的稳定性，选择如下陷波滤波器:

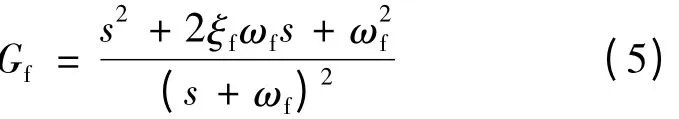
考虑柔性模态的不确定性，不妨取ωf= 1．05ωr，ξf= 0．05，即柔性模态没有完全消除，存在误差。考虑陷波滤波器之后，控制框图如图2 所示。

图2 PD 与陷波滤波控制框图

增加陷波滤波器之后的PD 控制性能如图3 所示，从图3 中可以看出，柔性模态存在时，闭环系统仍然稳定，阶跃响应的镇定时间小于0．001 s，但是超调达到30%，不完全满足性能指标。

风是气象学研究、大气科学研究和气候研究中最重要的参量之一。准确及时的风场数据可以提高长期天气预报的准确性，提高对飓风等恶劣天气跟踪及登陆预报的准确性。大气风场对于气候学和气象学的研究、大气动力学的研究、数值天气预报、环境监测、风能发电和军事航空安全等方面起着重要的作用。目前对大气风速测量的激光雷达多采用多普勒效应，该类激光雷达称为多普勒激光雷达。

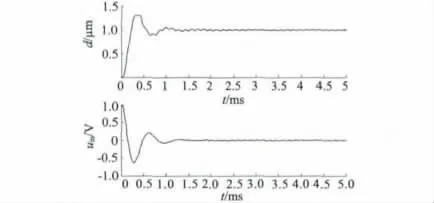
图3 PD 与陷波滤波控制性能及控制信号

再考虑传感器噪声，噪声为均方根0．1 μm 的白噪声，如图4(a)所示，对阶跃信号的跟踪如图4(b)所示，从图4 中可以看出，白噪声使闭环系统失去了稳定性。

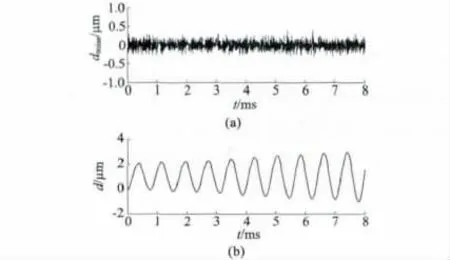
图4 测量噪声及PD 联合陷波滤波的控制性能

2 滞后超前补偿、PD 及陷波滤波联合控制

2.1 滞后超前补偿及陷波滤波

在噪声和扰动存在时，为了保证系统的稳定性，考虑超前滞后补偿器，如式(6)所示，并根据音圈电机Bode 图设计超前滞后补偿器参数［］。

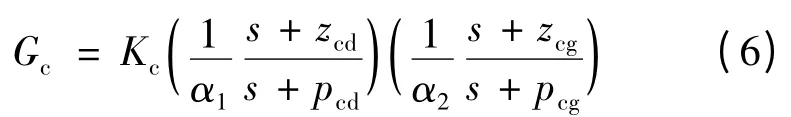
式中:zcd和pcd为超前补偿零点、极点，zcg和pcg为滞后补偿零点、极点。

先设计超前部分，再设计滞后部分。选择穿越频率ωc= 800·2π，Kc= 0．4。

ωc处待补偿的相位极限:

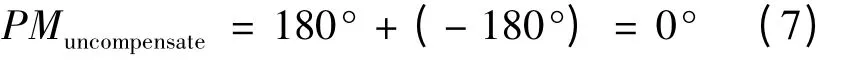
考虑40°的相位裕度，超前补偿需要提供的相位偏移量Φmax如下:

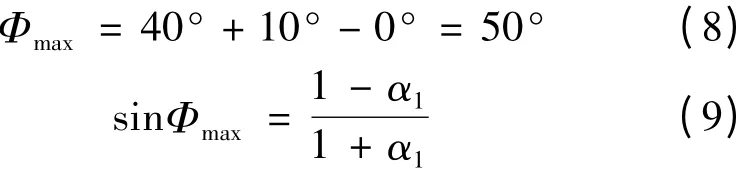
根据式(9)可得超前零极点比例α1:

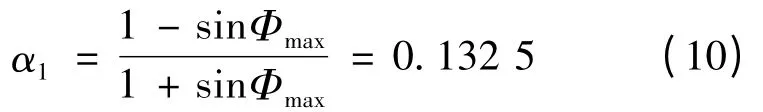
超前补偿的零点zcd:

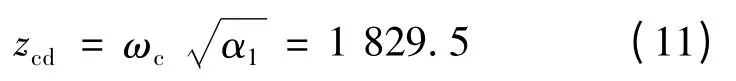
超前补偿的极点:

超前补偿后，系统的带宽增加，需抑制穿越频率ωc对应幅值到0 dB，G(jωc)Glead(jωc)= 8. 88 dB ，对应的滞后零点、极点比例α2如下:

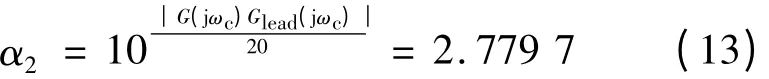
滞后补偿零点zcg:

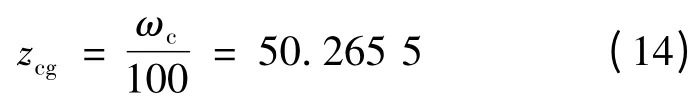
滞后补偿极点pcg:

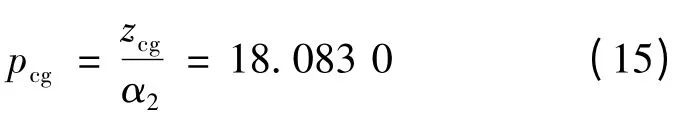
最终得到的超前滞后补偿如下:

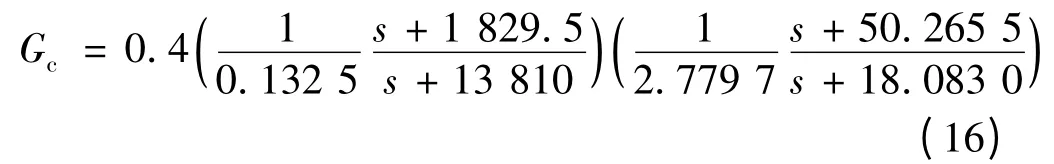
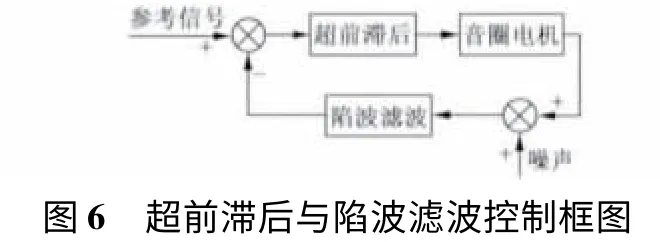
超前滞后补偿器Bode 图如图5 所示，控制系统框图如图6 所示。

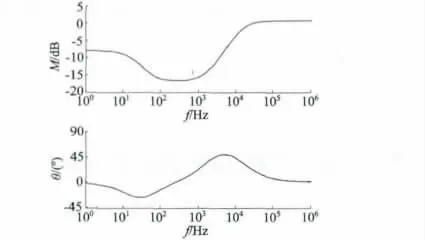
图5 超前滞后补偿Bode 图

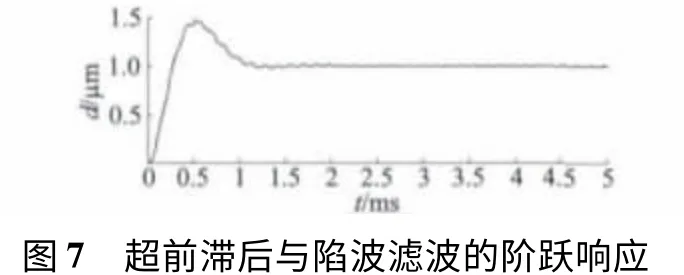
超前滞后补偿与陷波滤波的阶跃响应如图7 所示，从图7 中看出，镇定时间小于0．001 s，但是超调达到46%，需要增加新的控制环节来降低超调。

2.2 超前滞后补偿、PD 及陷波滤波联合控制

同时采用超前滞后补偿、PD 控制、陷波滤波，并且采用上述设计的参数，如图8 所示。

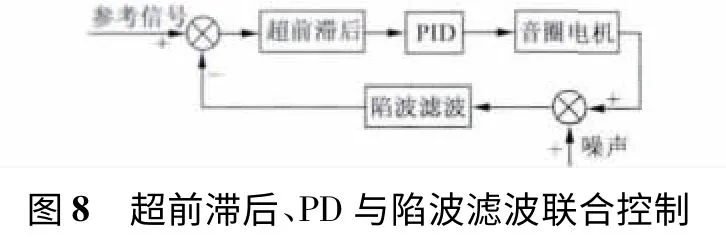
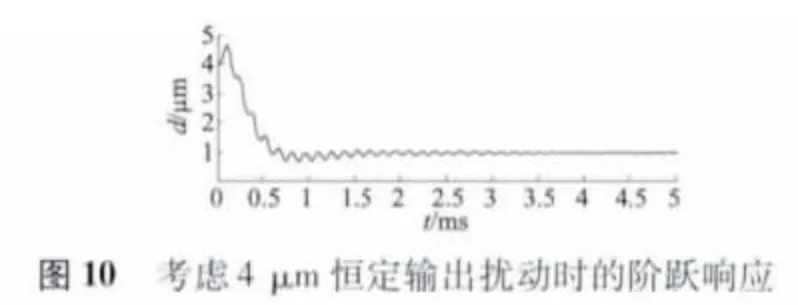
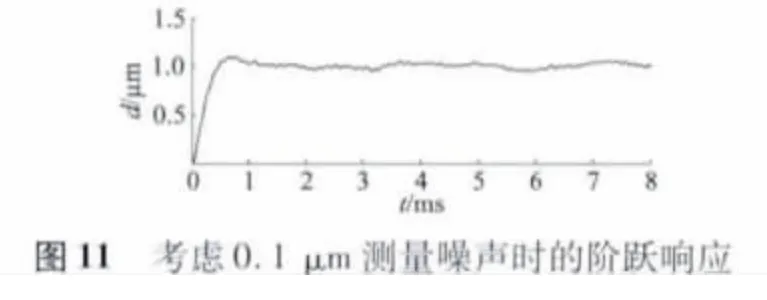
不考虑传感器噪声和扰动的阶跃信号性能如图9 所示，从图9 中可以看出，音圈电机在0．001 s 内达到稳定值，超调小于5%，满足性能指标要求。考虑4 μm 的恒定输出扰动，阶跃信号性能如图10 所示，控制系统对扰动仍有很好的抑制作用;考虑均方根0．1 μm 的传感器噪声，阶跃信号性能如图11 所示，输出在0．001 s 之后误差在5% 以内，满足了阶跃跟踪性能。

3 结 语

柔性模态使PD 控制器发生溢出，与陷波控制器联合控制可以满足镇定时间要求，但不满足超调的要求，本文设计了超前滞后补偿器，与PD 和陷波滤波器联合控制，阶跃信号的超调小于5%，镇定时间小于0．001 s，当存在输出恒值扰动及传感器噪声时，控制器仍然能够保持性能。

［1］ Roger W．Future hard disk drive systems［J］．Journal of Magnetism and Magnetic Materials，2009，321:555－561．

［2］ Venkataramanana V，Ben M C，Tong H L，et al．A new approach to the design of mode switching control in hard disk drive servo systems［J］．Control Engineering Practice，2002，10:925－939．

［3］ Wua S，Tomizuka M．An iterative learning control design for self －servowriting in hard disk drives［J］．Mechatronics，2010，20:53 －58．

［4］ Katsuhiko Ogata．Modern control engineering［M］．3rd ed．New Jersey:Prentice Hall，1997．

［5］ Franklin G，Powell J，Emami－Naeini A．Feedback control of dynamic systems［M］．6th ed．New Jersey:Prentice Hall，2009．