SH波入射下半空间垂直界面附近对称圆孔的动应力分析
杨 杰
(上海电机学院 机械学院, 上海 200245)
SH波入射下半空间垂直界面附近对称圆孔的动应力分析
杨 杰
(上海电机学院 机械学院, 上海 200245)
采用复变函数和“镜像”的方法,对双相介质半空间垂直界面附近含有对称圆形弹性孔洞,在稳态入射SH波作用下的动应力情况进行分析。首先,采用“镜像”的方法,构造问题所需的Green函数和散射波场表达式;其次,采用界面“契合”的技术,建立含有无穷未知力的第一类Fredholm积分方程组,并通过有效截断求解该方程组;最后,给出圆形孔洞周边的动应力集中系数的具体算例分析。结果显示,波数比和圆孔到垂直边界的距离均对孔洞周边动应力集中系数有一定程度的影响。
SH波; 垂直界面; 圆形孔洞; 镜像; 动应力集中系数
随着科学技术的快速发展和新型材料的广泛使用,将不可避免地在材料上开孔、加入转角等以满足功能上的需求。然而,由于几何不连续性,在动载荷作用下这些介质缺陷将产生应力集中现象,进而影响材料的宏观力学性能,故对于在动荷载作用下应力集中问题的研究一直是力学研究人员探讨的热点问题之一[1-3],其中,采用弹性波散射理论对介质缺陷附近的动应力集中情况的研究已经有相对成熟的理论和方法。20世纪70年代,Lee[4]等采用波函数展开方法,对均匀各向同性半空间中含有洞室对SH波的散射响应进行了研究。1991年,刘殿魁[5]等提出复变函数方法,对无限半空间凹陷地形对SH波的散射问题进行了进一步的研究和讨论。2003年,梁建文[6]等采用Fourier-Bessel级数展开方法,对地下隧道在稳态SV波入射下的地表反应问题进行了研究。2007年,梁建文[7]等对Wolf理论进行拓展,解决了弹性层状半空间对SH波的散射问题。2010年,Lee[8]等采用多极Trefttz方法,对薄板中含有多个圆形孔对弹性波的散射问题进行了研究。以上这些研究方法的提出及应用,为弹性波散射理论问题的研究提供了理论基础。由于SH波相对SV波、P波等对应问题的求解要简单得多,故近年来对介质中各种缺陷对SH波的散射问题研究比较常见[9-11]。然而,对于复杂边界介质中含有各种缺陷在SH波作用下的散射问题研究成果并不多见。2006年以后,史文谱[12-13]等采用复变函数和Fourier级数展开方法,对直角域中含有各种缺陷的问题进行了研究。
本文主要采用复变函数和“镜像”的方法,对双相介质半空间垂直界面附近含有对称圆形弹性孔洞在稳态入射SH波作用下的动应力情况进行了分析,其属于具有复杂边界的界面动力学研究范畴。该问题求解的难点在于Green函数以及散射波场位移表达式的构造,由于圆形孔洞产生的散射波将会在半空间自由表面和双相介质垂直界面之间发生多次的反射,故直接构造满足边界条件的散射波场表达式变得尤其困难。本文的创新点在于提出“镜像”的方法,同时结合复变函数方法,构造出满足控制方程和边界条件的Green函数、散射波场表达式的解析解答。最后给出具体算例,讨论了波数比、圆形孔洞与垂直界面之间的距离对孔边动应力集中系数的影响。
1 理论模型
无限半空间介质由双相介质垂直界面分为左右两部分,稳态SH波由左侧空间入射,同时在左右两侧分别含有一个圆形弹性孔洞缺陷,其理论模型如图1所示。其中,SH波的入射角度记作α0;介质Ⅰ、Ⅱ的弹性模量和密度分别设为μ1、μ2和ρ1、ρ2;圆形孔洞半径设为R,其圆心到半空间水平表面与垂直界面的距离分别设为h和d。同时建立如图所示坐标系x1O1y1,x′O′y′,x″O″y″,x2O2y2,它们之间的关系如下:z1=z″+d,z′=z″-ih,z2=z″-d。
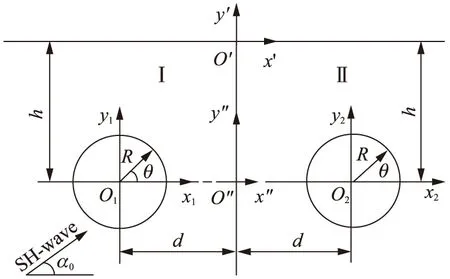
图1 SH波作用下双相介质半空间理论模型Fig.1 Theoretical model of bi-material half impacted by SH waves
2 控制方程和边界条件

(1)
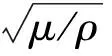
在极坐标系下,与式(1)对应的应力表达式为
(2)
在直角坐标系下,与式(1)对应的应力表达式为
(3)
对于问题的求解,首先采用“契合”[14]的方法,将双相介质半空间沿着垂直界面“剖开”,则半空间将被拆分为两个含有圆形孔洞的1/4空间。同时,需要在剖分面的左右两侧施加大小相等、方向相反的未知力f1和f2来满足原来垂直界面处位移和应力的连续性。契合模型如图2所示。可以看出,求解垂直界面处的未知反力是解答本文问题的主要任务之一。因此,本文采用Green函数方法解答此问题。

图2 契合模型Fig.2 Model of conjunction
2.1Green函数
含有圆形弹性孔洞的1/4空间,其垂直边界承受时间谐和的出平面点源荷载作用时位移函数的基本解答作为本文所需的Green函数。理论模型如图3所示。

图3 点源荷载作用下1/4空间理论模型Fig.3 Theoretical model of quarter space impacted by point source loads
Green函数满足式(1)所示的控制方程,而问题的边界条件如下:
(4)
在圆形孔洞周边满足应力自由条件,即
τr1z1|r1=R=0
(5)
Green函数可以看成点源函数单独作用1/4空间时产生的位移函数G(i)和由1/4空间中圆形孔洞对点源作用产生的散射位移函数G(s)的叠加。利用“虚设点源”的方法,位移函数G(i)的表达式为
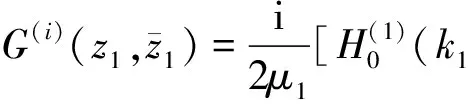

(6)
式中,

H(·)为Hankel函数。
在点源函数的作用下,由圆形孔洞所激发的散射波将会在1/4空间两个边界和孔洞之间发生多次的反射和散射效应,直接构造满足式(1)和式(4)的散射波场位移表达式是很困难的。因此,本文提出“镜像”的方法构造散射波场位移表达式,其具体思路如图4所示。

图4 “镜像”模型Fig.4 Model of image
以两个边界分别为对称面,将1/4空间问题转化为全空间问题,则散射波场位移表达式构造如下:
(7)
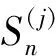
2.2定解积分方程组
稳态SH波入射下,双相介质半空间中入射波场位移表达式W(i)、反射波场W(r)以及折射波场位移表达式W(f)可以分别表示如下:

(8)
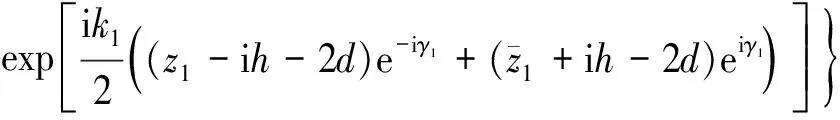
(9)

(10)
式中,W0、W1和W2分别是入射波、反射波和折射波的位移幅值,三者之间的关系如下:


同样地,根据“镜像”思想,散射波场位移表达式可以构造如下:
(11)

根据“契合”模型在双相介质界面处位移和应力的连续性,可以得到如下表达式:
(12)
式中,W(sΙ)和W(sΠ)分别为介质Ⅰ和介质Ⅱ中的散射波在剖分面处产生的位移;W(f1)和W(f2)分别为f1和f2在剖分面处产生的位移。利用
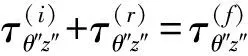
式(12)可以化为
(13)
根据Green函数具体表达式和式(13),定解积分方程组可以表示如下:

(14)

3 动应力集中系数
半空间垂直界面附近对称圆形孔洞在SH波作用下的动力特性分析的主要任务之一就是对圆孔周边动应力集中系数的求解[15]。在介质Ⅰ中,沿圆形孔洞周边的环向动应力集中系数的表达式为


(15)

通常,动应力集中系数表达式可以写成
(16)
式中,τ0=μ1k1W0为半空间入射应力的最大幅值。
4 算例分析与讨论
在具体算例中,给出图1所示模型介质Ⅰ中圆形弹性孔洞周边的动应力集中系数DSCF的分布情况。其中SH波入射波的位移幅值W0=1,介质Ⅰ和Ⅱ的弹性模量比值和波数比值分别为μ*=μ2/μ1和k*=k2/k1。
(1) 图5所示为SH波水平入射时,圆形孔边动应力集中系数DSCF随波数比k*的变化分布情况。取无量纲参数h/R=12.0,d/R=12.0。由图5(a)和(b)可以看出: 当SH波以低频入射时,孔边DSCF值随波数比k*的增加而变小,最大值发生在靠近半空间水平表面附近。由此说明,当SH波由相对较硬介质进入到相对较软介质中(k*gt;1.0)时,孔边DSCF值会变小,这正是由于软介质吸收更多能量造成的。由图5(c)和(d)可以看出,当SH波入射频率增加时,孔边DSCF值分布变化比较复杂,同时,DSCF数值随着波数比k*的增加有整体变大趋势。对比SH低频入射和高频入射两种情况,孔边DSCF最大值减小约21.60%。
(2) 图6所示SH波水平入射时,圆孔周边一点(θ=90°)DSCF随距离d/R的变化分布情况。取无量纲参数h/R=12.0。由图6(a)可以看出:“准静态”情况下(k1R=0.1),孔边一点DSCF值随距离d/R的增加而变化并不明显,同时曲线分布呈现波动性变化。当k*=1.0时,曲线近似为一条直线,此结果与文献[16]一致。然而,随着入射波数的增大,孔边一点DSCF曲线波动幅度加大,同时当距离d/Rgt;30附近,曲线有衰减趋势。由此说明,圆孔距离双相介质界面较远时,其对孔边DSCF的影响近似可以被忽略。

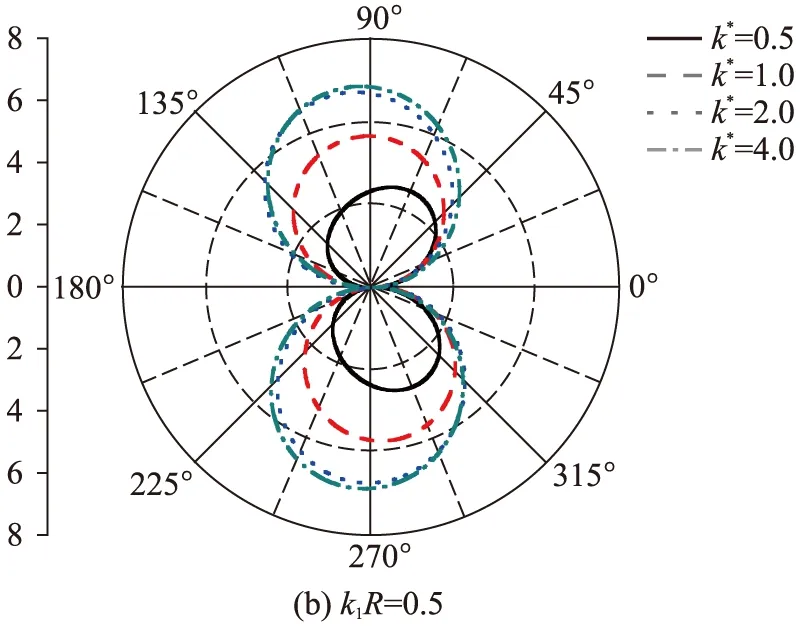


图5 SH波水平入射时,孔边DSCF的分布情况
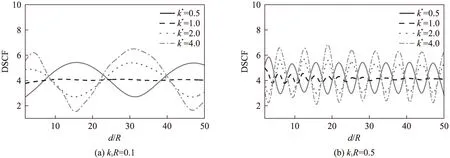

图6 SH波水平入射时,孔边一点DSCF的分布情况(θ=90°)Fig.6 Distribution of DSCF on a point of circular hole edge when SH waves are incident horizontally
5 结 语
本文主要采用复变函数和“镜像”的方法,求解了双相介质半空间垂直界面附近含有对称圆形弹性孔洞对稳态入射SH波的散射问题,同时,对孔边的动应力分布情况进行了分析讨论。从具体算例可以看出,不同的介质波数和孔洞到垂直边界的距离远近等因素都会对孔边的动应力集中系数的分布有一定影响。因此,在相应问题的研究中应予以重视。同时,本文算例分析结果可以为设计和工程实践等提供理论参考。
[1] 王 铎,汪越胜.界面动力学研究近况[J].上海力学,1993,14(4): 1-15.
[2] Pao Y H.Elastic waves in solids.ASME Journal of Applied Mechanics,1983,50(4): 1152-1164.
[3] Golub M V,Zhang Chuanzeng,Wang Yuesheng.SH-wave propagation and scatteing in periodically layered composites with a damaged layer[J].Journal of Sound and Vibration,2012,331(8): 1829-1843.
[4] Lee V M,Trifunac M D.Response of tunnels to incident SH-wave. Journal of Engineering Mechanics,1979,105(1): 643-659.
[5] Liu D K,Han F.Scattering of plane SH-waves by a cylindrical canyon of arbitrary shape.Int J Solid Dynamics and Earthquake Engineering,1991,10(5): 249-255.
[6] Liang Jianwen,Zhang Hao,Lee V W.A series solu-tion for surface motion amplification due to underground twin tunnels: incident SV waves[J].Earthquake Engineering and Engineering vibration,2003,2(2): 289-298.
[7] Lee W M,Chen J T.Scattering of flexural wave in thin plate with multiple circular holes by using the multipole trefttz method.International Journal of Solids and Structures,2010,47(9): 1118-1129.
[8] 梁建文,巴振宁.弹性层状半空间中沉积谷地对入射平面SH波的放大作用.地震工程与工程振动,2007,27(3): 1-9.
[9] Tsaur D H,Chang K H,Hsu M S.An analytical approach for the scattering of SH waves by a symmetrical V-shaped canyon: deep case[J].Geophysical Journal International,2010,183(3): 1501-1511.
[10] Xia T,Sun M,Hua W.Multiple scattering of plane SH wave by double-row of elastic pile as barries for vibration isolation[J].World Information on Earthquake Engineering,2011,27(1): 142-147.
[11] Chen J T,Lee J W,Shyu W S.SH-wave scattering by a semi-elliptical hill using a null-field boundary integral equation method and a hybrid method[J].Geophysical Journal International,2012,188(1): 177-194.
[12] Shi Wenpu,Liu Diankui,Song Yongtao.Scattering of circular cavity in right-angle plane space to steady SH-wave.Applied Mathematics and Mechanics,2006,27(12): 1619-1626.
[13] 史文谱,刘殿魁,宋永涛.直角平面区域内固定圆形刚性夹杂问题的Green函数解.固体力学学报,2006,27(2): 207-212.
[14] 刘殿魁,林 宏.SH波对双相介质界面附近圆形孔洞的散射[J].固体力学学报,2003,24(2): 197-204.
[15] 鲍亦应,毛昭宙,刘殿魁.弹性波的衍射与动应力集中[M].苏先樾,译.北京: 科学出版社,1993: 3-24.
[16] 林 宏,刘殿魁.半无限空间中圆形孔洞周围SH波的散射[J].地震工程与工程振动,2002,22(2): 9-16.
Dynamic Stress Analysis for Symmetrical Circular Holes Near Vertical Interface Impacted by SH Waves in Bi-material Half Space
YANGJie
(School of Mechanical Engineering, Shanghai Dianji University, Shanghai 200245, China)
A dynamic stress analysis for symmetrical circular holes near a vertical interface in a bi-material half space is performed using a methods of complex function and image. Expressions of Green’s functions and scattering waves are obtained with the aid of an image method. A series of Fredholm integral equations containing unknown forces are derived using an interface conjunction. The equations are solved using an effective truncation. Numerical examples for dynamic stress concentration around the edge of the circular hole are given. Numerical results demonstrate that the distribution of the dynamic stress concentration factor is influenced to some degree by the wave number ratio and distance between the circular hole and the vertical interface.
SH waves; vertical interface; circular hole; image; dynamic stress concentration factor
2095-0020(2013)05 -0262-06
O 347.4; O 348
A
2013-07-16
国家自然科学基金项目资助(10972064);上海电机学院重点学科资助(12xk501)
杨 杰(1985-),女,讲师,博士,主要研究方向为波动理论及应用,E-mail: yangj@sdju.edu.cn

