高超声速滑翔飞行峰点高度确定方法

吕石, 唐硕, 闫晓东

(1.西北工业大学 航天学院, 陕西 西安 710072; 2.航天飞行动力学国家重点实验室, 陕西 西安 710072)

高超声速滑翔飞行峰点高度确定方法

吕石1,2, 唐硕1,2, 闫晓东1,2

(1.西北工业大学 航天学院, 陕西 西安 710072; 2.航天飞行动力学国家重点实验室, 陕西 西安 710072)

针对快速准确获取高超声速滑翔峰点高度的问题,提出了一种在给定初始速度大小的情况下峰点高度计算的迭代算法。考虑将动压和过载约束条件统一到热流率约束条件上,首先在常数速度条件下估算了峰点高度,然后依据峰点高度容许误差迭代计算了峰点高度的修正值,最后通过算例进行了验证。仿真结果表明,该算法计算速度快、精度高,具有同时处理三种约束条件的通用性。

峰点高度; 高超声速滑翔飞行器; 迭代算法

0 引言

一般的高超声速滑翔飞行器(HGV)均采用助推火箭发射,并在达到滑翔条件时与助推火箭分离,进行无动力滑翔飞行。在无动力滑翔过程中,HGV要满足各种弹道约束,主要有热流率、过载以及动压约束。这三种约束条件在滑翔过程中也可以通过滑翔飞行走廊进行描述[1]。HGV在无动力滑翔飞行的最高点处具有的能量可以通过速度和高度的二维空间进行描述。但是,在一定初始速度下,为了满足三种过程约束,滑翔飞行最大高度(即峰点)不能太大[2-3]。若峰点过高,在滑翔初始段高度会迅速降低,将以较大的速度进入稠密大气层,使得热流率、过载和动压不满足约束。此外,飞行峰点高度决定了HGV与助推器的分离条件,所以如何快速准确地确定峰点飞行高度对于HGV的分离条件研究以及弹道设计具有重要意义。高超声速技术验证飞行器HTV-2的第二次飞行试验中,在滑翔段开始不久就与地面失去了联系,据事后分析认为可能是由于与助推器分离高度较高导致滑翔段初始飞行过程中HTV-2的表面温度过高,动压太大,最后导致热防护结构破坏,所以研究HGV飞行峰点高度具有重要意义。

由于在滑翔段飞行过程中HGV的飞行状态变化较为剧烈,同时飞行的状态不易通过解析方法直接精确预测,因此,峰点高度很难通过解析方法直接精确得到。文献[4]讨论了通过响应面法和牛顿法等搜索算法确定峰点高度,但是响应面法需要构造近似模型[5],牛顿法需要计算和储存海森矩阵,当海森矩阵不是正定时会导致搜索任务失败[5]。

本文针对HGV滑翔段飞行过程中,满足热流率、过载以及动压约束条件的峰点高度确定,提出了一种无需构造近似模型和储存海森矩阵的快速精确的迭代算法,此外,算法将分析满足三种约束条件的处理方式统一到满足热流率约束条件的分析方法上,使其对三种约束条件的处理具有通用性。

1 动力学模型

典型的HGV飞行剖面如图 1所示。AC段表示整个滑翔段弹道,A点表示滑翔段的峰点,B点表示HGV滑翔飞行过程中弹道倾角首次等于零的状态,AB段称为滑翔过程的初始下降段。该段飞行初期飞行器气动力较小,飞行器会快速下降进入稠密大气层,B点的热流率和动压可能是滑翔段飞行过程中的极值点,与本文将研究的内容密切相关。

图1 HGV滑翔段的典型飞行剖面示意图Fig.1 Typical lateral gliding flight curve of HGV

考虑地球曲率,不考虑地球自转,假设HGV倾斜角大小保持为零,在弹道坐标系中纵向质点动力学和运动学方程[6]可以描述为:

(1)

(2)

(3)

2 峰点高度确定方法

文献[3]指出,当飞行器CAV-L[6]在A点初始速度较大时,其滑翔段的热流率峰值一般出现在B点附近。基于此特性,本文研究的迭代算法首先需要估算满足三种约束条件的峰点高度初值;然后确定迭代计算过程中初始高度的修正量;最后根据计算结果容许误差要求得到峰点高度。

2.1 峰点高度的估算

根据CAV-L的初始下降段的飞行特点,文献[2-3]对滑翔段弹道进行了仿真,从仿真结果可知,在给定的初始速度条件下,飞行器在初始下降段飞行过程中的速度变化量比峰点处的速度小很多,因此,可以通过初始下降段的速度常值假设来获取峰点高度的初始估计值。

令a1=-gcosθ+V2cosθ/(H+Re),则式(1)可转化为:

(4)

同样,将式(3)变为:

V=(dH/dt)/sinθ

(5)

在初始下降段飞行过程中,飞行器速度保持常值,即V=V0,那么a1变化较小,同样可以用常值表示,即等于飞行器初始状态对应的值a0。

将式(4)两端同时除以V02并且代入式(5),两端同时积分可得:

(6)

飞行器在初始下降段飞行过程中,A点的弹道倾角为零,同时B点处的弹道倾角也接近于零,故式(6)等号左半部分积分结果近似为零,从而变换等式右端可以得到:

(7)

采用大气密度公式[7]为:

(8)

(9)

在初始下降段飞行过程中,由于HGV的最大热流率、过载以及动压通常接近于B点,在飞行器到达B点附近时,飞行器应该满足热流率峰值条件、过载峰值条件以及动压峰值条件。

热流率峰值条件为:

(10)

式中,RN为飞行器端头半径;C1为常值;Vc=

过载峰值条件为:

(11)

动压峰值条件为:

(12)

则热流率峰值对应的最低点大气密度为:

(13)

过载峰值对应的最低点大气密度为:

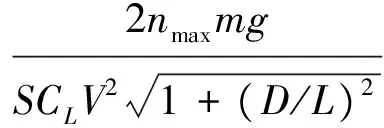
(14)

动压约束值对应的最低点大气密度为:

ρmax(q)=2qmax/V2

(15)

要保证初始下降段飞行过程满足以上三个约束条件,则需要选择三者中最小的大气密度来获得初始下降段的最低点高度,即

ρmax=min[ρmax(Q),ρmax(n),ρmax(q)]

(16)

因此满足约束的最低点高度为:

(17)

取Hf=Hmin,结合式(9)可以得出初始高度的解析表达式为:

(18)

当最低点高度高于35 km时,ze-βH0/(βa0)对H0的大小影响已很小,因此,在初步确定最高点的过程中可以忽略ze-βH0/(βa0)对H0计算的影响,所以,式(18)可以简化为:

(19)

根据三种约束条件和HGV在峰点处的速度,就能够通过式(19)估算出HGV滑翔段飞行峰点高度。

2.2 高度修正量的计算

峰点高度估算方法是建立在HGV初始下降段速度常值的假设基础上,而弹道积分过程中,速度大小会发生变化。但是,基于H0的峰点高度基准,在初始下降段飞行过程中,若峰点高度大小增加范围较小时,高度的增加量对最低点处速度大小影响较小[8],因此,若峰点高度的变化量在一个较小的区间内,可以假设终端速度为常量。

又由:

(20)

在整个初始下降段飞行过程中,由于大气阻力作用,将导致Qmax0

若使Qmax1=Qmax,则预测最低点的大气密度为:

(21)

式中,Hmin1为预测最低点的高度。

根据最低点速度常值假设,结合式(5)、式(11)、式(12)、式(20)和式(21)可知:

(22)

式中,nmax0为第一次弹道积分的过载峰值;nmax1为预测下一次弹道积分的过载峰值;qmax0为第一次弹道积分的动压峰值;qmax1为预测下一次弹道积分的动压峰值。

由式(10)～式(12)可知,动压和过载的修正值可以通过转化为热流率的修正方式获得,可取

(23)

式中,nmaxi为第i次弹道积分的过载峰值;qmaxi为第i次弹道积分的动压峰值。

当过载或动压约束条件不满足时,可以将通过修正热流率峰值约束条件进行迭代计算,即

(24)

对比式(20)和式(21)可以得出:

Hmin1=Hmin0-2 ln(Qmax/Qmax0)/β

(25)

(26)

式中,aver0为首次弹道积分获得的最大热流率处HGV铅垂方向上的加速度;aver1为预测下一次迭代计算的最大热流率处HGV铅垂方向上的加速度。

当初始高度增加ΔH时,则式(7)将改写为:

a0(H0+ΔH-Hmin1)=

(27)

忽略初始下降段起始阶段的气动力,积分式(27),结合式(25)并化简得:

ΔH≈-(aver0+aver1)ln(Qmax/Qmax0)/(βa0)

(28)

预测下一次计算峰点高度为H1=H0+ΔH,再对弹道进行积分计算,求取下降过程中的热流率峰值。

则第i次(i=1,2,…)迭代计算的峰点高度为:

Hi=Hi-1+ΔH

(29)

式中,aver(i-1)为第i-1次弹道积分最大热流率处飞行器铅垂方向上的加速度;aver(i)为预测的第i次弹道积分最大热流率处飞行器铅垂方向上的加速度;Qmax(i-1)为第i-1次弹道积分过程中的热流率峰值。

在满足Qmax(i)≤Qmax的条件下,峰点高度的迭代计算容许误差为:

σ%=|Hmax(i)-Hmax(i-1)|/Hmax(i-1)×100%

(30)

2.3 迭代计算流程图

在给定速度初值条件下,计算满足热流率、过载及动压约束的峰点高度迭代流程图如图 2所示。

图2 迭代计算流程图Fig.2 Flow chart for iterative calculation

3 算例

以通用飞行器CAV-L为仿真对象,可以对算法计算速度、精度以及处理三种约束条件的通用性进行验证。在初始下降段飞行过程中,飞行器的约束值为Qmax=1 000 kW/m2,nmax=4,qmax=400 kPa,飞行器端头半径为0.1 m,迎角为常值20°[7],升力和阻力系数变化较小,因此CL取定值0.6,CD取定值0.35。

3.1 计算速度和计算精度验证

若初始速度为6 500 m/s,在初始下降段中主要将三种约束条件统一到热流率约束条件。选择迭代计算峰点高度精度为0.5%,计算结果如表 1所示。

表1 不同迭代次数的计算结果Table 1 Results of the different iterations

在表 1中,Hi表示第i次迭代的初始高度,Qmax(i)表示第i次迭代的热流率峰值。由结果可知,迭代第3次结束时,算法的精度就已得到保证,若需要更高的精度,增加迭代次数就能满足条件。因此,算法的快速性和准确性得到了较好的验证。

3.2 通用性验证

选择不同的初始速度,在初始下降段飞行过程中可能出现不同的约束条件决定峰点高度,通过4次迭代计算所获得的峰点高度和热流率、过载以及动压峰值如表 2所示。

表2 不同初始速度条件下飞行器峰点高度的计算结果Table 2 Calculating results of peak altitude on the condition of different initial velocities

由表 2可知,当初始速度不同时,峰点高度将取决于不同的约束条件,在表中,当初始速度大于6 000 m/s时,峰点高度由热流率约束条件决定;当初始速度小于5 800 m/s时,峰点高度由过载约束条件决定。本文的算法在迭代计算中将三种约束条件统一到热流率约束条件上,通过转换可直接采用统一的峰点高度估算和修正公式,通过表2仿真计算结果较好地验证了迭代算法的通用性。

4 结束语

通过仿真结果验证,本文提出的算法不仅计算精度高,计算速度快,而且对于多约束条件的处理方法具有较好的通用性。算法不仅能为HGV滑翔弹道设计的总体参数选择提供参考,而且也能为滑翔段的热防护系统以及结构系统设计提供技术支撑。下一步的工作是在气动力系数为常值的假设基础上,需要对更为复杂的气动模型情况进行研究,推导出更为理想的迭代修正计算模型。

[1] Shen Zuojun,Lu Ping.Onboard generation of three-dimensional constrained entry trajectories[J].Journal of Guidance,Control,and Dynamics,2003,26(1):110-121.

[2] 雍恩米,唐国金,陈磊.高超声速无动力远程滑翔飞行器多约束条件下的轨迹快速生成[J].宇航学报,2008,29(1):48-49.

[3] 王智.高超声速滑翔飞行器再入制导研究[D].西安:西北工业大学,2012.

[4] 康炳南.通用航空器轨迹优化设计研究[D].西安:西北工业大学,2010.

[5] Simpson T W,Peplinski J D,Koch P N.On the use of statistics in design and the implications for deterministic computer experiments[R].Sacramento,California:ASME Design Engineering Technical Conferences,1997.

[6] 吴了泥,黄一敏,贺成龙.基于动压剖面的再入弹道解析解[J].弹箭与制导学报,2009,29(6):173-177.

[7] 张毅,肖龙旭,王顺宏.弹道导弹弹道学[M].长沙:国防科学技术大学出版社,2005:245.

[8] 雍恩米.高超声速滑翔式再入飞行器轨迹优化与制导方法研究[D].长沙:国防科学技术大学,2008.

(编辑：方春玲)

Themethodtodefinethealtitudeofhypersonicglidingpeak

LÜ Shi1,2, TANG Shuo1,2, YAN Xiao-dong1,2

(1.College of Astronautics, NWPU, Xi’an 710072, China; 2.National Key Laboratory of Aerospace Flight Dynamics, Xi’an 710072, China)

Under the condition that the initial velocity is given, an iterative algorithm is provided to rapidly calculate the exact hypersonic gliding altitude. Considering that the dynamic pressure and the load constraints are unified to the heating rate constraints, we firstly estimate the altitude of the peak at the assumption that velocity is a constant, and then calculate the corrected value of peak altitude according to the altitude tolerance. Eventually, a numerical example is simulated to demonstrate the validation of the proposed algorithm and the result shows that it calculates quickly and exactly, and has the ability to deal with these three constraints simultaneously.

altitude of peak; hypersonic gliding vehicle; iterative algorithm

V412

A

1002-0853(2013)04-0349-05

2012-11-05;

2013-04-03; < class="emphasis_bold">网络出版时间

时间:2013-06-06 12:25

吕石(1988-)，男，四川南充人，硕士研究生，研究方向为飞行器设计。