越肩发射前战斗机攻击轨迹研究

李浩亮, 张斌, 左星星

(空军工程大学 航空航天工程学院, 陕西 西安 710038)

越肩发射前战斗机攻击轨迹研究

李浩亮, 张斌, 左星星

(空军工程大学 航空航天工程学院, 陕西 西安 710038)

越肩发射(OTS)可以增大导弹的截获区。战斗机攻击尾后目标时,为了达到导弹的最佳发射点,提出了一种基于勒让德伪谱法(LPM)攻击轨迹规划方法,实时规划战斗机的攻击轨迹,及时调整飞机状态。首先通过数据链获取目标的运动参数;分析了采用越肩发射方式的攻击轨迹规划问题,建立了攻击轨迹规划最优控制模型;引入勒让德伪谱法将控制模型离散为非线性模型;最后利用snopt工具箱进行了仿真验证。仿真结果表明,该方法可以为战斗机规划一条既能准确发射导弹又满足机动性要求的攻击轨迹。

越肩发射; 轨迹规划; 勒让德伪谱法; 最优控制

0 引言

越肩发射能力是下一代空空导弹必须具备的一个重要特性,导弹的攻击范围将扩大到以战斗机为中心的360°空间内。为了提高越肩发射导弹的命中概率,除了大力提高导弹的性能外,还可以通过其他方法。文献[1]采用本机智能机动策略增大越肩发射截获区的方式,将越肩发射截获区增大了122%;文献[2]首先利用LPM具有解算精度高、计算速度快等优点求解最优航迹控制问题。本文用LPM求解采用越肩发射方式战斗机最佳的攻击轨迹控制，为战斗机选择一条最优攻击轨迹。在考虑尾后目标机动的情况下建立轨迹规划最优控制模型,通过LPM将最优控制问题转化为非线性规划问题,最后进行了仿真验证。

1 基本理论分析

LPM是数值解法中的一种直接配点法,其原理是先求解Legendre多项式一阶导数,将其映射到时间区间上,作为插值节点,将节点处的状态变量和控制变量作为参数,用拉格朗日插值多项式拟合轨迹上各时刻状态变量和控制变量,将动态最优控制问题转化为静态参数优化(NLP)问题[3]。

2 目标运动参数的获取

由于战斗机体积的限制,现在还不能为战斗机安装后视雷达,虽然三代机一般都装有后视传感器,但也只能很粗略地估算出尾后敌机的大致方位。为了计算出战斗机的最优攻击轨迹,需要知道尾后目标精确的运动参数,这就需要通过数据链从第三方探测器(预警机或地面站)获取目标参数。

数据链的功能是向战斗机F提供目标的北、东、地位置坐标xT,yT,zT;速度VT;相对北向航向角φT。飞机的运动参数可以由机上传感器获得,分别为xF,yF,zF,VF,φF。则目标相对于战斗机的距离矢量为:

De=(xT-xF,yT-yF,zT-zF)

将距离矢量转换到飞机坐标系中可得:

Df=Tf,eDe

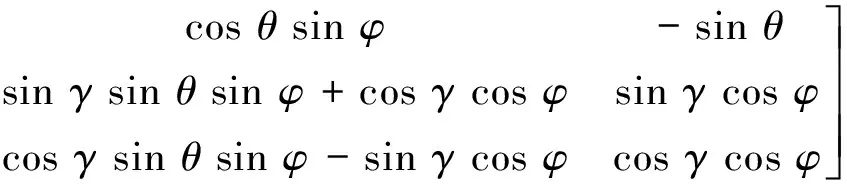
式中，各参数定义见文献[4]。

目标相对战斗机的航向:Δφ=φF-φT。确定了目标相对战斗机的准确位置和目标的运动方向,火控计算机就可以在导弹的全向截获区内选择一条最佳的攻击轨迹,并适时给出导弹发射的指令,这样既能保证导弹以最大概率命中目标,又能保证战斗机尽快脱离敌机导弹的攻击区。典型的导弹全向截获区如图1[5]所示。

图1 越肩发射导弹的全向截获区Fig.1 All-aspect capture zone of OTS missile

3 战斗机攻击轨迹模型建立

3.1 战斗机模型及无量纲化处理

本文采用第三代战斗机的六自由度模型,结合目标的运动参数和导弹的性能参数,通过火控计算机解算实时获取战斗机所需要的控制信息。

使用越肩发射方式实时规划攻击轨迹时,引入无量纲化概念,对战斗机模型进行无量纲化处理,这样能够更加有效地提高计算速度和精度,经过无量纲化处理后的战斗机模型为:

(1)

战斗机要做机动,就要有控制量。本文选取推力比P、迎角α、横滚角γ作为控制量u=[P,α,γ]T,这3个量就可以保证战斗机在三自由度空间内运动。选取战斗机在地理坐标系中的位置(x,y,z)、速度V、轨迹倾斜角γgj、轨迹方位角χ作为状态量x=[x,y,z,V,γgj,χ]T。其余参数说明见文献[6]。战斗机在正常飞行时,控制量和部分状态量应满足:

(2)

3.2 战斗机攻击轨迹目标模型建立

为了使导弹在最短时间内转弯,同时考虑到战斗机自身的操控性能,建立如下目标函数模型,并进行无量纲化处理:

(3)

3.3 最优控制模型建立

根据式(1)～式(3),为获得满足战斗机飞行性能和越肩发射条件的最优控制信息,将攻击轨迹规划问题转化为最优控制问题:

(4)

4 基于LPM的最优控制模型离散化

利用LPM解决动态最优控制问题,首先将动态最优控制问题转化为静态参数优化问题(即非线性规划问题),然后进行寻优求解。

4.1 区间映射

将函数的勒让德多项式在[-1,1]内展开,勒让德零点的范围即为[-1,1]。因此利用LPM时需要将式(4)的限制区间映射到[-1,1]区间内,其映射模型为:

(5)

通过式(5),可将式(4)转换为:

(6)

4.2 勒让德离散理论

对于N阶勒让德多项式LN(τ)有:

LN(τ)=

(7)

取勒让德零点τk(k=1,2,…,N-1),令τ0=-1,τN=1,取拉格朗日插值基函数:

(8)

可得:

(9)

因此,对于任意函数F(τ),τ∈[-1,1],其N阶勒让德插值多项式为:

φj(τ)

(10)

由式(9)可知:

FN(τk)=F(τk) (k=0,1,…,N)

(11)

(1)微分离散化

对式(10)求导,可得其在点τk处的导数:

(12)

其中:

(2)积分离散化

(13)

其中:

ωk=2/{N(N+1)[LN(τk)]2} (k=0,1,…,N)

4.3 最优控制模型离散化

通过分析,利用上面的公式,可将最优控制模型式(6)中控制量、状态量变化为:

(14)

由式(11)可知:

ak=u(τk)=uN(τk),bk=x(τk)=xN(τk)

(15)

最后将最优控制模型离散为:

(16)

5 仿真分析

战斗机攻击轨迹规划是一个大型非线性规划问题,本文使用Matlab的snopt工具箱解算非线性模型,可得到对应时刻的控制信息,通过处理可得到战斗机沿攻击轨迹飞行时所需的控制量,飞行员根据控制量操控战斗机飞行完成越肩发射。

假设战斗机初始位置:xF0=100 km,yF0=20 km,zF0=4 km;初始控制量:P0=0.3,α0=3°,γ0=1°;初始状态量:V0=260 m/s,γgi0=0°,χ0=100°;战斗机雷达散射面积:δmin=0.40 m2,δmax=2.15 m2;目标初始位置:xT0=150 km,yT0=10 km,zT0=4.8 km;初始状态为:VT=300 m/s,φT=90°;且目标指向战斗机机动飞行。

限制条件:200 m/s≤V≤400 m/s;-40°≤γgj≤40°;-180°≤χ≤180°;0≤P≤1，P为推力比(即推力与最大推力的比值);-2°≤α≤30°;-70°≤γ≤70°。仿真终止条件:武器发射高度h=5.0 km;γgjF=0°;|αF|≤15°;|γF|≤30°;时域长度T=20 s;

N=5。

图2～图4为火控计算机解算的战斗机攻击轨迹的控制量变化,飞行员根据这些信息操控飞机飞行。从曲线变化可以看出,实时解算出的战斗机最优攻击轨迹控制量均满足给定的限制条件。

图2 战斗机推力变化Fig.2 Curve of thrust

图3 战斗机迎角变化Fig.3 Curve of attack of angle

图4 战斗机滚转角变化Fig.4 Curve of roll angle

图5～图7为飞行员根据控制信息操控战斗机飞行得出的状态量,即飞行参数,可知当t=45 s时,战斗机发射导弹攻击目标;在t<45 s时间内,火控计算机在充分考虑后半球威胁、战斗机性能和导弹攻击区动态变化的基础上,实时地规划战斗机攻击轨迹,飞行员根据控制信息调整战斗机姿态,最后根据攻击指令,发射导弹,图中状态量指标均满足限制条件和最后攻击条件。其攻击轨迹如图8所示。

图5 战斗机速度变化Fig.5 Curve of speed

图6 攻击轨迹方位角变化Fig.6 Curve of track azimuth

图7 攻击轨迹倾斜角变化Fig.7 Curve of track bank angle

图8 战斗机的攻击轨迹Fig.8 Curve of attacking trajectory

由图8还可以看出,战斗机采用越肩发射方式攻击目标,不再需要将目标置于攻击前半球,因此本身并不需要做过大的机动,导弹发射后战斗机即可机动脱离,各状态量也趋于平缓。

6 结束语

本文分析采用越肩发射方式战斗机攻击轨迹规划过程,建立了攻击轨迹最优控制模型。利用勒让德伪谱法将复杂的最优控制问题转化为NLP问题,将搜索空间限制在有限时域内,保证了精度。通过仿真分析肯定了战斗机具备越肩发射能力的优越

性,而火控系统能为战斗机选择一条攻击轨迹，既能保证击毁敌机又能保障我机安全,使越肩发射具备更高的可靠性。

[1] 高劲松,邹庆元,陈哨东,等.采用本机智能机动策略增大越肩发射截获区[J].系统仿真学报,2007,19(13):2948-2950.

[2] Fahroo F,Ross I M.Costate estimation by a Legendre pseudospectral method[J].Journal of Guidance,Control,and Dynamics,2001,24(2):270-277.

[3] Paul W.Aircraft trajectory planning for terrain following incorporating actuator constraints[J].Journal of Aircraft,2005,42(5):1358-1362.

[4] 周志刚.航空综合火力控制原理[M].北京:国防工业出版社,2008:28-29.

[5] 姜欢,刘彦,邢晓岚,等.空空导弹越肩发射全向攻击区的计算[J].飞行力学,2007,25(3):26-29.

[6] Anisi D A.On-line trajectory planning for aerial vehicles:a safe approach with guaranteed task completion[R].AIAA-2006-6107,2006.

(编辑：方春玲)

Fighterplane’sattackingtrackprogrammingofover-the-shoulder

LI Hao-liang, ZHANG Bin, ZUO Xing-xing

(Aeronautics and Astronautics Engineering College, Air Force Engineering University, Xi’an 710038, China)

The over-the-shoulder(OTS) can enlarge the capture zone of missile. When attacking the target behind the fighter, a method of attacking track programming of fighter plane based on Legendre pseudospectral method(LPM) is proposed to reach the best emitting point, programming attacking track in real time, regulating the state of fighter. Firstly, obtain the parameter of the target through data link; analyze attacking track programming using OTS, building optimal control model of attacking track programming; scattering the control model into nonlinear model with the method of LPM. Finally, simulation is done based on snopt tools, the result shows that the computer can program an attacking trajectory which can accurately fire the missile and meet the requirements of fighter’s maneuverability.

over-the-shoulder; track programming; LPM; optimal control

V249

A

1002-0853(2013)04-0308-05

2012-11-14;

2013-03-21; < class="emphasis_bold">网络出版时间

时间:2013-06-06 13:21

航空科学基金资助(20095196012)

李浩亮(1989-),男,河南郑州人,硕士研究生,研究方向为航空火力指挥与电子综合。