相位匹配双阵元去噪算法的IP设计

王 晨，吴 鹏，张海龙

（沈阳师范大学 科信软件学院，沈阳 110034）

0 引 言

随着科学技术的不断发展，目前的电子系统功能强大结构复杂。由于系统存在复杂的结构，开发系统的时候一般将系统分解成多个层次，每个层次内部又由多个模块组成，在实际的开发过程中软IP和硬IP都可以作为开发过程中用到的组件，可以将其放入资源库中以备系统需要时调用［1－3］。以集成平台为基础的设计方法是一种稳定的IP框架设计方法，本文采用的是AlteraQuartus II设计平台，对相位匹配双阵元去噪算法进行IP核的设计。

1 相位匹配双阵元算法步骤分析

相位匹配双阵元算法是采用双传感器来接收空间中的信号，利用双阵元间的信号相位差来同步信号，然后抵消掉噪声，达到去除噪声提取信号的目的［4－5］。对于双阵元获取信号的数学表达式为

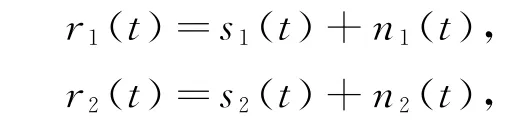
式中：r1（t）和r2（t）表示阵元实际接收到的信号，它是真实信号与噪声的和信号，是已知的信号，s1（t）和s2（t）是需要检测还原的信号即期望信号，而n1（t）和n2（t）是各向同性的随机噪声。由于双阵元间的距离很近，信号采集的时候又是同一时刻，所以可以认为n1（t）≈n2（t）＝n（t），这样就可以得到这样的数学表达式

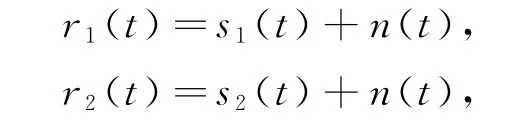
两式子两边做傅立叶变换可以得到如下形式：

其中：R1（ω）是r1（t）的傅立叶变换，S1（ω）是s1（t）的傅立叶变换，N（ω）是N（t）的傅立叶变换，其他类同。为了研究问题方便，将该表达式采用极坐标形式的频域表示：

其中：φ1和φ2、α1和α2、β分别为接收到实际信号、期望信号和噪声信号的相位角，分别是ω的函数，分别为接收到实际信号、期望信号和噪声信号谱的幅值。这里的相位角是接收到实际信号、期望信号和噪声信号傅立叶变换后虚部与实部比的反正切值。

由于阵元间存在距离，双阵元接收信号的相位是有差异的，接下来是计算相位差，相位差是由于波达时间不一样造成的，计算出波达时间的差，如果双阵元间距离为d，原始信号s（t）与二元阵的法线的夹角为θ，对于远场信号而言，波前到达的时间是不一样的，时间差用式表示，c为波速。所以相位差为信号角频率与时间差的乘积。于是可以得到那么傅立叶变换后的极坐标方程就可以写成如下形式［6－7］：

这样方程就可解了，对方程求解，信号是未知数，得到下式：

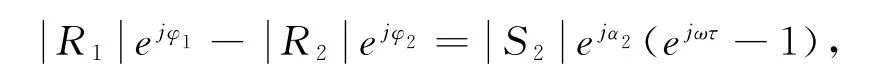
对等号两边写成频域的复数形式得到下式：

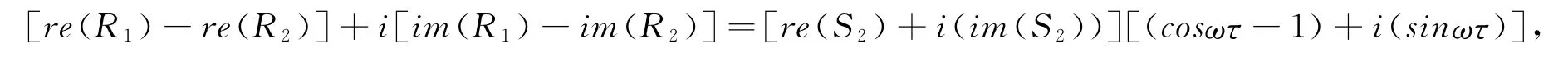
式中：re（＊）表示取复数的实部，im（＊）表示取复数的虚部，ω为待测信号的角频率，由复数相等的概念得知等号两边的实部和虚部分别相等，因此得到如下方程组

对方程组求解得到

将上面的步骤归纳起来可以用图1表示。

图1 双阵元相位匹配计算步骤

从图1可以得出双阵元相位匹配的计算步骤，首先是阵列中的双阵元在同一时刻进行信号的采集，由于信号存在相差，所以要对每个阵元采集的信号进行傅立叶变换，变换后将信号相位对齐，得到计算表达式（1）与式（2），由接收信号的实部和虚部就可以计算出期望信号的实部和虚部，再经过逆傅立叶变换得到时域期望信号。这个过程的计算步骤是在获取信号之后，对获取信号做傅立叶变换，得到获取信号的傅立叶变换的实部和虚部，再由获取信号的实部和虚部计算出期望信号的波形。

2 位匹配双阵元算法IP核结构设计

按照相位匹配双阵元算法的内容，IP核的设计从功能上分为输入、处理、输出和控制4个部分。其中输入部分就是信号采样的过程，采样数据存储在存储器中，处理部分就是将存储器中的采样信号读取出来进行处理，处理过程包括双阵元采集的两路信号进行傅立叶变换，变换后获取实部和虚部，计算出期望信号的实部和虚部，进行逆傅立叶变换，最终还原出期望信号。输出部分是将处理部分处理的结果输出，实际上输出的信号同样存储在输出存储器中，控制部分的作用是通过控制信号协调其他各个部分有序的工作。

在IP核设计结构中，需要特殊说明的部分是控制部分，首先该部分是IP核设计的核心，其次该部分控制着整个数据的流向，其作用是让各个部分协调的工作。控制部分控制处理部分将输入寄存器的数据取出，而输入寄存器的采样数据还需要二进制倒置，这是因为采用了快速傅立叶变换对于基2蝶形算法的需要，这就要在处理部分进行运算之前将输入部分的输入数据进行二进制倒置排序，排序后的数据才可以被处理部分使用。

在处理部分进行傅立叶运算的时候还有一个旋转因子需要给出［8－9］，而每一次给出的的值并不相同，旋转因子的值都需要存储在寄存器中，准备为每次计算使用，它需要的控制信号和信息都由控制部分产生。

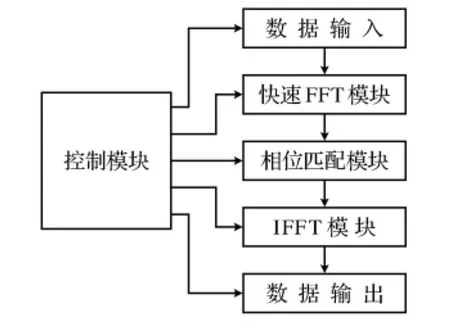
图2 IP核整体结构图

根据这4个部分的描述给出整体IP各个模块的之间的结构图2。

从图2可以得到IP核的整体结构设计为6个模块，它们分别是控制模块、数据输入模块、快速傅立叶变换模块、相位匹配模块、逆傅立叶变换模块和数据输出模块。其中控制模块是协调其他模块顺序工作，数据输入模块存储了输入数据，将这些数据提供给快速傅立叶变换模块，快速傅立叶变换模块进行傅立叶变换，将变换后的数据提交给相位匹配模块，相位匹配模块处理信号，计算出期望信号的实部与虚部，将数据交给逆傅立叶变换模块进行逆傅立叶变换，再将变换后的时域信号存入数据输出模块中。

数据输入模块实际上是用RAM来实现的，其功能就是存储采样后的数据，内部结构简单。快速傅立叶变换模块的结构相对复杂，其结构由图3给出。

图3 FFT整体结构图

在图3中看到的该FFT分成了8个部分，这几个部分协调工作，控制部分将A／D转换后的信号数据存放到RAM，把按顺序排好的输入数据一条条读出来，输入到二进制倒置模块，进行二进制倒置，倒置后的数据按照位置直接存入到二进制倒置RAM中。ROM中存入的是旋转因子，具体的数值是由快速傅立叶变换的点数决定的，此设计中是一个固定的值，取512点的快速傅立叶变换，因此ROM中的数据个数为21＋22＋…＋29的和，它们是已经计算好的固定不变的值，所以存储在ROM中。快速傅立叶变换使用傅立叶变换公式对二进制倒置数据与旋转因子进行层层迭代，迭代过程的中间运算数据放入临时数据存储器中，实际上临时数据存储器有一个特点，存储空间被一分为二，目的是将基2变换的数据按奇偶分类存放，便于数据的提取和计算。最后将计算的结果放入输出寄存器也就是图3的快速傅立叶变换后的数据RAM。

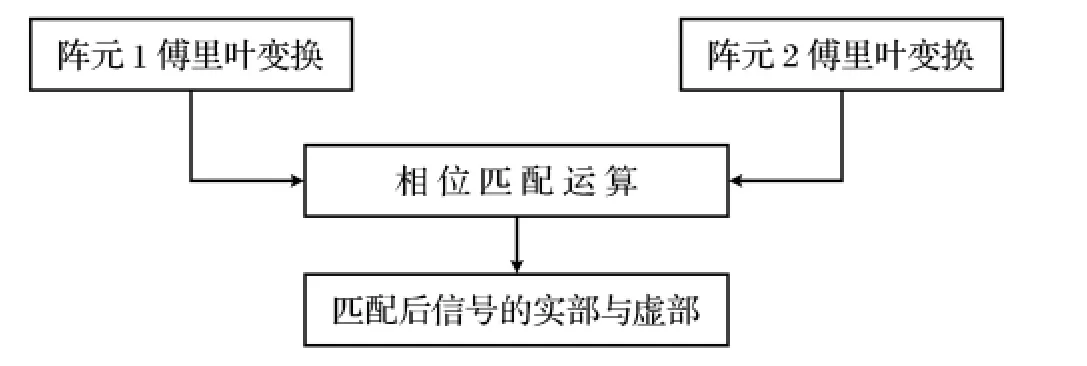
图4 相位匹配模块结构图

相位匹配模块将傅立叶变换后的数据进行匹配运算，其结构如图4所示。

从图4中看到相位匹配算法是将阵元1与阵元2对接收信号傅立叶变换的结果应用到表达式（1）和（2）中，得出期望信号的实部和虚部。图5是FFT模块的顶层原理图，由ram模块、exchange模块、rom模块和fft模块构成。其中fft模块控制其他几个模块的动作，使得其他模块协调的处理数据。首先fft模块通过读地址线与读允许信号控制ram（inst1），将其中的数据读到exchange模块，再通过时钟和使能信号线控制exchange模块进行二进制倒序，通过写控制信号线将处理好的数据存储到另一个ram（inst3）模块中，然后利用使能和地址信号控制rom模块输出旋转因子，同时利用读信号和地址信号控制ram（inst3）模块将数据读入到fft模块，进行基2的快速傅立叶变换运算，将最终运算结果的实部和虚部输出。

图5 FFT模块原理图

图6是FFT模块的仿真。该仿真采用频率是50Hz和100Hz的正弦波的叠加波形作为输入信号，输入的点数为1 024点，然后加入随机噪声，使信噪比为5dB，对未加入噪声的信号和加入噪声的信号进行傅立叶变换，从仿真图上可以看到，非加噪信号经过傅立叶处理后，信号变得非常清晰，加噪声信号经过FFT输出后仍然可以清晰的看到信号的存在，所以对信号的检测结果是很清晰的，在对加噪信号进行傅立叶处理后仍然可以看到在不同的频率上的一些振幅的无规则起伏，这就是噪声的能量在不同频率上的分布情况。

图6 FFT模块功能仿真

图7的快速傅立叶变换的输出做了取模处理，在Modelsim仿真中做了模拟量无符号整型处理。

为了更好的说明快速傅立叶变换的处理过程，在图7中对快速傅立叶处理后的数据进行获取实部和虚部处理，再通过模拟仿真显示出快速傅立叶变换的图形特征。

图8为快速傅立叶变换的时序仿真，仿真结果经过了去刺处理，效果很好，虽然有少量的毛刺存在，但对处理并没有太大的影响。

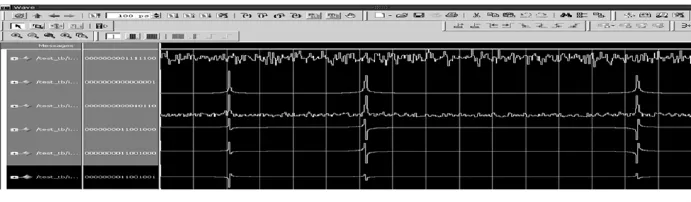
图7 FFT输出功能仿真

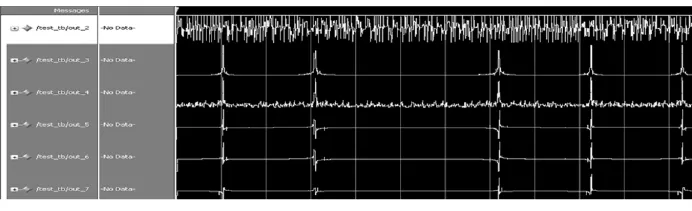
图8 FFT输出时序仿真

3 相位匹配双阵元去噪算法IP核仿真

相位匹配双阵元去噪算法实际上是从传感器上接收信号，对同一个信号进行两路的傅立叶变换，然后消去噪声还原出信号。在IP核的结构上可以分为两路傅立叶变换模块，双阵元相位匹配模块和逆傅立叶变换模块，而这几个模块可以采用流水线方式进行工作。实际上将该算法按照功能分成了3个功能模块，每个模块可以独立运行，各个模块之间又有输出输入的关系，这样就可以形成并行操作和流水线方式的工作，图9为各个模块间的原理图。

图9 双阵元相位匹配算法原理图

从图9可以看到双阵元相位匹配模块是主控模块启动到了控制模块的作用，完成相位匹配算法，同时向其他模块发送控制信号，协调各个模块间的工作。输入是2路傅立叶变换后的实部和虚部，输出有控制输出和数据输出，控制输出含有傅立叶变换允许输出（enfft），傅立叶变换读允许输出（enfftr）。分别控制2个输入模块fft1和fft2，数据输出模块是计算后得到期望信号的实部和虚部，输出到逆傅立叶变换模块，经逆傅立叶变换后输出时域数据。

同样从图9可以得到处理过程的并行关系，首先两路信号的傅立叶变换处理可以同时进行，所说的同时是指可以一起进行的并行操作。它们的处理结果输送给双阵元相位匹配处理模块，当双阵元相位匹配处理模块进行工作时，傅立叶变换模块又可以与并行操作，当双阵元相位匹配处理模块将数据处理完后启动逆傅立叶变换模块，这时3个功能模块就可以采用并行的流水线方式进行工作。

图10是双阵元相位匹配算法的功能仿真图，其反映了算法固化于硬件后，由硬件处理信号的结果。

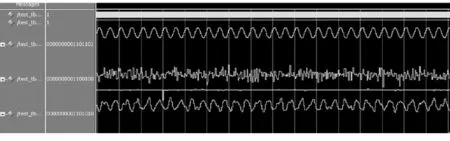
图10 双阵元相位匹配算法的功能仿真

在图10中采用100Hz频率的正弦波，加入－1dB的信噪比噪声，采样点数为10K，在该图中从上到下分别显示了原始信号，原始信号加入噪声，经过双阵元相位匹配算法处理后的功能仿真图。可以看到基本上可以恢复原信号的特征。

由于达到一个十分完好的时序仿真有很多的约束条件，首先在时钟跳变到来时数据是否已经准备好，其次在时钟跳变后对信号进行操作，信号的不变性是否满足，也就是信号的保持时间是否足够，再有信号到达指定逻辑并达到指定电平的延时是否充分，还有时钟的偏移与抖动等误差，这些都使得系统工作起来不稳定，产生的干扰对系统的性能影响很大。

对于高频信号由于布线中的电容的存在，这样就存在着信号的串扰，串扰问题对信号的最终处理都会产生不良的影响。同时由于高频的存在，时钟频率也会很高，这样在单个时钟周期就越小，就要求信号的传输速度要很快，除了传输速度，信号的稳定速度和撤销速度都要求很高，图11是对图10的时序仿真。

图11 双阵元相位匹配算法的时序仿真

从图11可以看到由于实际信号在FPGA器件中通过逻辑单元连线时，一定存在延时，延时的大小不仅和连线的长短和逻辑单元的数目有关，而且也和器件的制造工艺、工作环境等有关。因此，信号在器件中传输的时候，所需要的时间是不能精确估计的，当多路信号同时发生跳变的瞬间，就产生了“竞争冒险”。这时，往往会出现一些不正确的尖峰信号，这些尖峰信号就是“毛刺”。另外，由于FPGA以及其他的CPLD器件内部的分布电容和电感对电路中的毛刺基本没有什么过滤作用，因此这些毛刺信号就会被“保留”并传递到后一级，从而使得毛刺问题更加突出。可见，即使是在最简单的逻辑运算中，如果出现多路信号同时跳变的情况，在通过内部走线之后，就一定会产生毛刺［10－11］。而现在使用在数字电路设计以及数字信号处理中的信号往往是由时钟控制的，多数据输入的复杂运算系统，甚至每个数据都由相当多的位数组成。这时，每一级的毛刺都会对结果有严重的影响，对于多级的设计，那么毛刺累加后会影响整个设计的可靠性和精确性。

去除毛刺的方法有很多种，其目的都是使数据稳定的时候再进行处理，这样就减小的毛刺产生的几率，本文不做过多的处理。

4 结 论

本文给出了相位匹配双阵元算法IP核的设计方法。将算法进行了分层分析，对各个层次之间模块的先序与并行关系给出了说明，同时对各个层次的模块设计给出了剖析和具体的实现过程。对IP核内部的傅里叶变换模块进行了功能和时序仿真，验证了模块的设计合理性，对IP核整体进行了功能仿真和时序仿真，其仿真结果与理论值相符，验证了IP核设计的正确性。

［1］吴松龄.IP核技术在航天系统的发展与展望［J］.航天标准化，2012（2）：1－3.

［2］崔旭晶，马平全.基于SOPC的触控屏控制器IP核设计与实现［J］.电子工程设计，2012，20（14）：166－169.

［3］刘文超，黄汉华，唐文龙.基于SoPC的红外解码IP核设计与实现［J］.现代电子技术，2012，35（12）：4－6.

［4］吴鹏，李晶皎，王爱侠，等.相位匹配噪声估计的高阶谱去噪方法［J］.小型微型计算机系统，2010，31（12）：2381－2384.

［5］吴鹏，王爱侠，李晶皎.信号相位匹配噪声估计的小波去噪方法［J］.计算机科学，2010，37（7）：285－287.

［6］吴鹏.线性调频信号的相位匹配去噪方法［J］.沈阳师范大学学报：自然科学版，2009，27（2）：206－208.

［7］于湘珍，朱维杰，张龙军.利用信号相位匹配原理抵消相干干扰的性能分析［J］.空军工程大学学报，2008，9（3）：58－62.

［8］WU Peng，LI Jingjiao.The noise removal on rebound signal of linear fequency［C］∥Proceedings 2009 9th internatianal conference on hybrid intelligent systems HIS，2009：7－9.

［9］PEI S C，DING J J.Relations between fractional operationsand time－frequency distributions，and their applications［J］.IEEE Transon SP，2001，49（8）：1638－1655.

［10］吴正国，夏立，尹为民.现代信号处理技术［M］.武汉：武汉大学出版社，2003：15－75.

［11］康磊，宋彩利，李润洲.数字电路设计及Verilog HDL实现［M］.西安：西安电子科技大学出版社，2010：385－395.