Delay-dependent absolute stability analysis of improved Lurie control system with multiple delays
, , ,
(1.School of Mathematics and System Science,Shenyang Normal University,Shenyang 110034,China;2.Math department,Shenyang Guangquan Middle School,Shenyang 110141,China)
0 Introduction
It is well known that time delay is often an significant source for instability in various engineering systems[1-14].The stability problem of Lurie control system with time-delay has been studied by many researchers[11-14].
In this paper,we study the stability problem for Lurie control system with multiple delays,respectively.Based on the division of the delay,The system matrixBi(i=1,2,…,m)are decomposed.an suitable of Lyapunov functional is proposed to study this class of system.Some improved delay-dependent Lyapunov functionals are derived by employing an integral-inequality.An example is presented to illustrate the effectiveness for some existing results.
1 Problem statement
Consider the Lurie control system with multiple time delays of the form

wherex(t)∈Rnis state vector;A,Bi(i=1,2,…,m)∈Rn×n,D,C∈Rn×mare consent matrices;hi≥0(i=1,2,…,m)are time delays.φ(t)is a continuous vector valued initial condition.The nonlinearitiesfj(·)(i=1,2,…,m)satisfy the finite sector condition

In order to receive the main results,which begin with the following lemma
Lemma[2]Given any constant appropriately dimensioned matricesR,N,X,and scalarh>0 and vector valued functionsf(x)andηsuch that the following integration is well defined,then
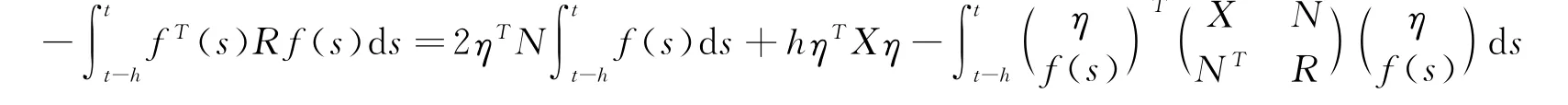
2 Stability analysis
In order to improve the bound of the discrete-delayhi,let us decompose the matrixBiasBi=Bi1+Bi2(i=1,2,…,m),whereBi1,Bi2(i=1,2,…,m)are constant matrice.Then the original system∑can be represented in the form of a descriptor system with discrete and distributed delays

namel

with the initial conditon∑.
LetD(xt)be a new operator,we have

In order to guarantee that the difference operatorD(xt):C[-max{τi},0]→Rngiven by(4)is stable(i.e.difference equationD(xt)=0is asymptotically).
TheoremGiven positive scalarshi,system ∑ with nonlinearity located in the finite sector[0,K]is absolutely stable if there exist positive definite matricesP>0,Qi1>0,Qi2>0,Zi1>0,Zi2>0,Ki>0(i=1,2,…,m),diagonal matrixR=diag{r1,r2,…,rm}≥0,a scalarε>0and appropriately dimensioned matricesMij=…]T,i=1,2,…,m;j=1,2,…,N,satisfying


ProofFor∑ with nonlinearity located in the sector[0,K],condition(2)is equivalent to

Let us choose the following Lyapunov functional candidate for the system∑,

whereP>0,Qi1>0,Qi2>0,Zi1>0,Zi2>0,Ki>0(i=1,2,…,m)and diagonal matrixR=diag{r1,r2,…,rm}≥0are to be determined.
Then,taking the derivative ofV(t)with respect to along the solution of system ∑,at the same time,employing the lemma,schur complete and other mathematical technology,This theorem can be proved.The process can be omitted.
WhenD≡0,system ∑can reduce to the following linear system with multiple delays

Take the Lyapunov functional asV(t)=V1(t)+V2(t)+V3(t)+V5(t),whereV1(t),V2(t),V3(t)andV5(t)are defined in(6)~(10).
system ∑′is asymptotically stable.We can use theorom to prore this.
3 Illustrative example
ExampleConsider the system (1)with

This example was given in[10-14],The maximum value ofhmaxfor absolute stability of system(1)form is shown in table 1.Now we use the criterion in this paper to study the problem.Let us decompose matrixB1asB1=B11+B12as well as it did in[14],where

Solving LMI(5),table 1shows that the absolute stability criterion in this paper gives a much less conservative result than these in Refs.[10-14].

Table 1 Maximum upper bound of h for different Methods
4 Conclusion
The stability of Lurie control systems with multiple time-delays is investigated.By dividing the delay interval into n segments and choosing proper Lyapunov functional,the delay-dependent absolutely stable condition for Lurie control systems with multiple time-delay is received.The numerical example has shown significant improvement over some existing results.
[1]JACK H.Theory of Functional Differential Equation[M].New York:Spring,1977.
[2]HE Yong,WANG Qingguo,XIE Lihua,et al.Further improvemen of free-weighting matrices technique for systems with timevarying delay[J].Automat Control,2007,52(2):293-299.
[3]HE Yong,WU Min,SHE Jinhua.Parameter-dependent Lyapunov functional for stability of time-delay systems with polytopic type uncertainties[J].Automat Control,2004,49(5):828-832.
[4]WU Min,HE Yong,SHE Jinhua.New delay-dependent stability criteria and stabilizing method for neutral systems[J].Automat Control,2004,49(12):2266-2271.
[5]TIAN Junkang,ZHONG Shouming,XIONG Lianglin.Delay-dependent absolute stability of Lurie control systems with multiple time-delays[J].Appl Math Comput,2007,188(1):397-384.
[6]GAO Jie,XU Zhaodi.Guaranteed cost control of uncertain linear systems with both state and input delays[J].Journal of Shenyang Normal University Natural Science Edition,2009,27(4):408-412.
[7]CAO Jiuwen,ZHONG Shouming,HU Yuanyuan.Delay-dependent condition for absolute stability of Lurie control systems with multiple time delays and nonlinearities[J].J Math Anal Appl,2008,338(1):497-504.
[8]CAO Jiuwen,ZHONG Shouming.New delay-dependent condition for absolute stability of Lurie control systems with multiple timedelays and nonlinearities[J].Appl Math Comput,2007,194(1):250-258.
[9]QIU Fang,ZHANG Quanxin.Absolute stability analysis of Lurie control system with multiple delays:An integral-equality approach[J].Nonlinear Anal,2011,12(3):1475-1484.
[10]MIAN Xiaohong.Delay dependent conditions for absolute stability of Lurie type control systems[J].Acta Automat Sinica,1999,25(4):564-566.
[11]XU Bingji,LIAO Xiaoxin.Absolute stability criteria of delay-dependent for Lurie control systems[J].Acta Automat Sinica,2002,28(2):317-320.
[12]CHEN Dongyan,LIU Weihua.Delay-dependent robust stability for Lurie control systems with multiple time delays[J].Contr Theor Appl,2005,22(3):499-502.
[13]YANG Bin,CHEN Mianyun.Delay-dependent criterion for absolute stability of Lurie type control systems with time delays[J].Contr Theor Appl,2001,18(6):929-931.
[14]TIAN Junkang,ZHONG Shouming,XIONG Lianglin.Delay-dependent absolute stability of Lurie control systems with multiple time-delays[J].Appl Math Comput,2007,188(1):379-384.

