基于粒子群算法的重力张量反演研究

孙中科，朱自强，鲁光银，曹书锦

（中南大学 地球科学与信息物理工程学院，湖南 长沙 410083）

0 前言

在地球物理勘探中，常规的重力勘探仪器只能测量到重力位的垂向一阶导数，而重力梯度测量仪能够测量重力位的二阶导数，即重力梯度张量分量中独立的五个分量［1］。由于重力张量拥有的各种优异特征，国外对重力梯度张量特征的研究已经进入到较深的层次［2～5］。Vasco［6］建立了一组长方体模型，在下底埋深不同的条件下，对重力张量的三个对角线元素（Vxx，Vyy，Vzz）的反演结果特征进行了分析；Zhdanov［7］基于三维正则化条件下的收敛技术对重力梯度的全部张量数据做了反演。这种方法的特点是在正演拟合过程中，采用的是同体积同质心的球作为基本剖分单元，一定程度上简化了反演过程中的正演迭代计算。在对重力张量实测数据的去噪方面，Julio［8］首次提出将一维自适应引入小波滤波技术，这种方法在保留局部尖峰信号的同时，可以滤掉高频噪声；While［9］通过频谱分析方法，得到了重力张量的二维功率及其法则，该法则可用于判断所测得的重力梯度张量异常数据是否由地质原因引起；Kevin L.Mickus［10］通过对数据进行快速傅立叶变换（FFT），对垂向重力数据进行推导得到了全部的重力梯度张量数据。在此基础上，在重力梯度张量解释方面已有成功应用实例的还有功率谱反演方法［11］和欧拉褶积法［12］等。与国外相比，国内研究重力梯度张量的水平还处于比较落后的阶段，且国内对重力梯度的研究主要集中在单独计算某一个单独的梯度张量分量上，在确定场源边界上应用较多［13，14］，而在张量意义上的应用却很少。魏伟［15］给出了一种能够对断裂的重力异常数据进行改进的梯度解释方法；赵德军［16］对水平重力梯度分量的边值问题的级数解进行了推导；李姗姗［17］给出了基于重力矢量的Neumann边值问题和Dirichlet边值问题的解；刘尚余［18］在对卫星重力梯度数据处理的过程中引入了快速傅里叶变换。总的来说，国内重力张量的研究还出于起步阶段，但已经展现出良好的发展势头。

粒子群优化算法（简称PSO）是1995年Kenndey和Eberhart［19］提出的一种基于群体智能的优化算法。粒子群优化算法的特点是利用个体在解空间中的随机速度来改变个体，其解群相对进化代数而言，标尺暗处更强的随机性，其计算复杂度比其它算法低，搜索速度更快。吴招才等［20］将PSO算法应用于板状体磁异常的反演，并与遗传算法（GA）进行了比对；邱宁等［21］将混沌思想应用于PSO算法，利用混沌扰动的方法来解决PSO算法中的局部极值问题，并对磁法数据进行了反演，取得了一定的效果。

1 正演基础

重力梯度张量被定义为重力位［22］在各个方向的二阶导数。在笛卡尔坐标系条件下，假设重力位为V，则重力梯度张量可用一个3×3的矩阵来表示：

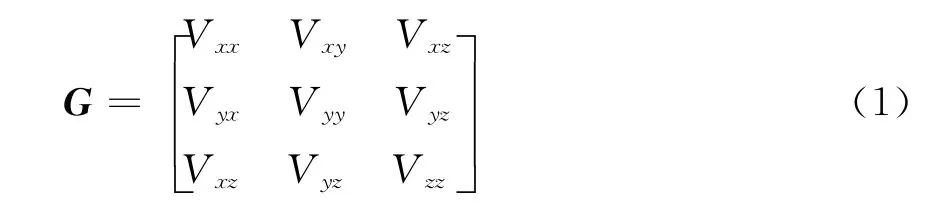
在无源空间内，引力的散度和旋度都为零，重力梯度张量矩阵为对称矩阵，所以有：Vxx＋Vyy＋Vzz＝0，Vxy＝Vyx，Vxz＝Vzx，Vzy＝Vyz，可以看出，重力梯度的九个张量中只有五个是独立的。重力梯度的国际标准单位为1／s2，但这个单位过于大，通常使用厄缶（E）作为重力梯度张量的量纲，1E＝1mGal／（10km）。

作者在本文中，将目标体划分为许多小的长方体，计算每个长方体的张量后叠加，长方体模型如图1所示。在图1中，（ζ1，η1，ξ1）、（ζ2，η2，ξ2）分别为长方体角点坐标；（x，y，z）为测点坐标。

布格重力异常及重力各个张量分量计算公式如下［23、24］：

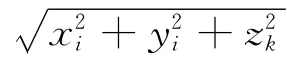
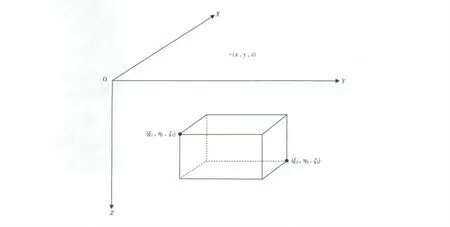
图1 长方体正演模型Fig.1 The forward model of rectangular parallelepiped

2 粒子群优化算法

粒子群优化算法［21］（PSO）来源于对鸟群有序且不可预测的运动特点进行抽象化，将群体中的每一个个体都看作搜索空间（解空间）中某一个粒子，分别代表着反演问题的每一个可行解，每一个粒子具有速度和位置两个基本属性。每个粒子都依据自身及周围粒子的迭代经验进行更新，即每一个粒子都通过评价自身最优解和群体的最优，来不断对自己的速度和位置进行改正，粒子的优劣程度（与反演模型的拟合程度）是通过对粒子所对应的适应度函数值确定的。粒子群算法求解过程不需要导数信息，只要给出的问题能够求出适应度函数值，就能够通过粒子自身的迭代进行求解，粒子群优化算法基本的迭代公式如下：

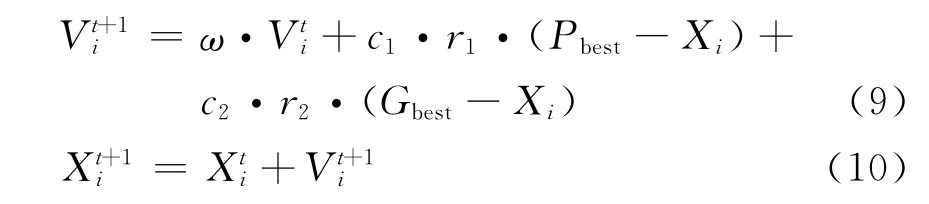
其中 t是迭代次数；i是粒子在群体中的编号。

为迭代第t次时候粒子i的速度。

式（12）为粒子迭代第t次时候编号为i粒子所在位置；Pbest是粒子i的个体最优位置；Gbest是解空间中全部粒子的最佳位置；r1和r2为［0，1］区间内均匀且独立分布的任意数；c1和c2为迭代过程的学习因子，用来控制每次粒子更新时的步长；ω为惯性权重因子，用来控制粒子继承上一代粒子特征的大小。式（9）是根据粒子自身位置、历史最优和全局最优位置来计算获得的最新速度。在迭代过程中，每一个粒子的速度都被限制在［－vmax，vmax］范围内，用以控制粒子的极值不能超出解空间。然后群体根据式（10）飞行到新的位置。具体流程如下［25］：

（1）初始化参数，包括惯性因子ω、学习因子c1和c2。

（2）随机产生M个粒子的种群，在允许范围内随机设置粒子的初始位置和速度。评价每一个粒子的适应值，由目标函数计算每一个粒子的适应度值并评价其优劣。

（3）粒子在解空间搜索，对每一个粒子，其本身的最优解记为Pbest。

（4）整个种群目前搜索到的最优解称为全局最优解记为Gbest。

（5）每个粒子根据式（9）、式（10）来更新自身的速度和位置，并把速度限制在［－vmax，vmax］范围内。

（6）检查终止条件（达到设定迭代次数或最优解满足条件），如果满足则终止迭代输出结果，否则返回步骤（3）。

3 重力张量粒子群优化反演

3.1 反演理论

地球物理反演问题可以表示为式（13）。

Gαβ＝Sαβ，σ （13）将Sαβ看作映射算子（即雅可比矩阵），σ为待测模型的密度参数，那么反演问题就是求已知观测数据Gαβ下通过S－1αβ求反演模型σ的一种运算。在重力张量单分量反演中，分别对式（13）中的模型观测数据和雅可比矩阵取相应的分量值即可。在包含全部张量的联合反演中，我们选取其中五个独立的分量（Vxx，Vxy，Vyy，Vxz，Vyz），令

式中 G为五个独立分量的观测值构成的矩阵；S为相应的几何函数构成的矩阵。分别用式（14）、式（15）代替式（13）中的两个矩阵，就得到重力全张量联合反演的关系式。

3.2 目标函数

反演过程可以归结为使如下最小二乘目标函数趋于极小：

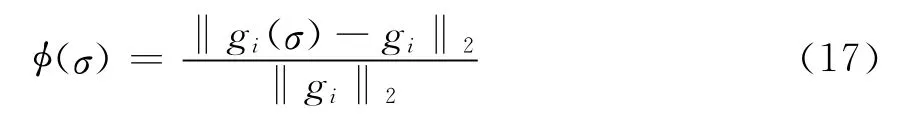
式中 gi（i＝1，2，…，n）为n个离散反演模型的观测值；gi（σ）（i＝1，2，…，n）为模型σ的理论正演场值在与gi点对应的n个离散采样值；σ为反演迭代中的模型参数。

3.3 模型试算

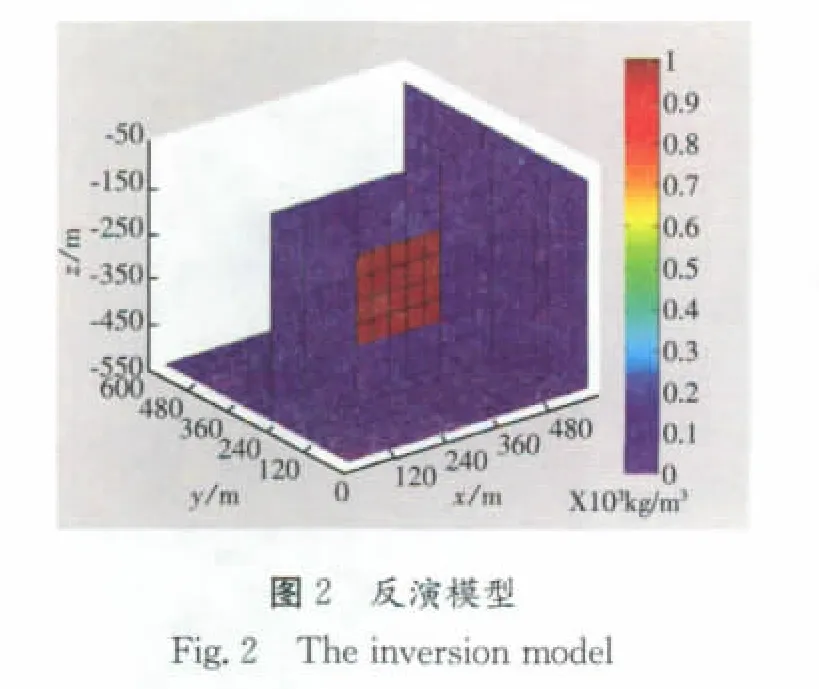
为了验证该算法的正确性，本文作者设计了如下目标体：将场源所在空间划分成15×15×10个基本物性单元，每个基本单元在x、y方向上的长度都为40m，z方向上设为为50m，目标体模型为一个大小为200×200×200的正方体，其顶面埋深为200m，剩余密度设定为1×103kg／m3，其余点的密度为“0”。地表的测网共有15×15＝225个测点，沿x、y方向的点距都为40m。

反演参数设置如下：惯性权重因子ω取阻尼惯性权重，为（0，1）之间的某个数，在反演中可以变化；学习因子c1＝c2＝2；初始种群数设置为模型单元个数的二倍；初始解的取值范围皆为（0，1）内的随机数；反演中将粒子速度限制在（0，1）范围内；迭代次数都设为500次。

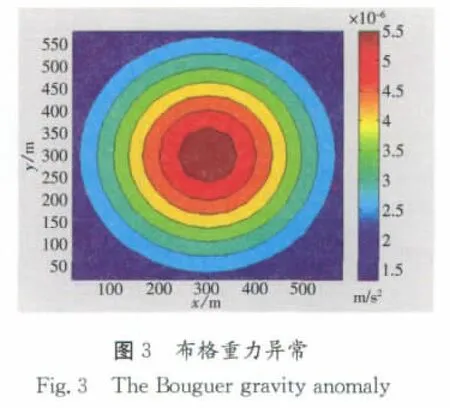
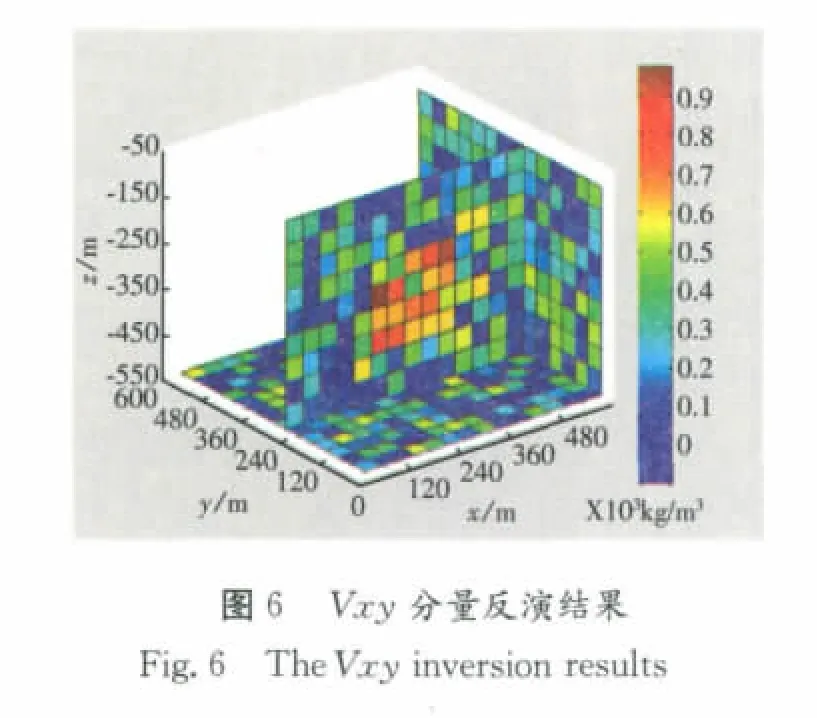
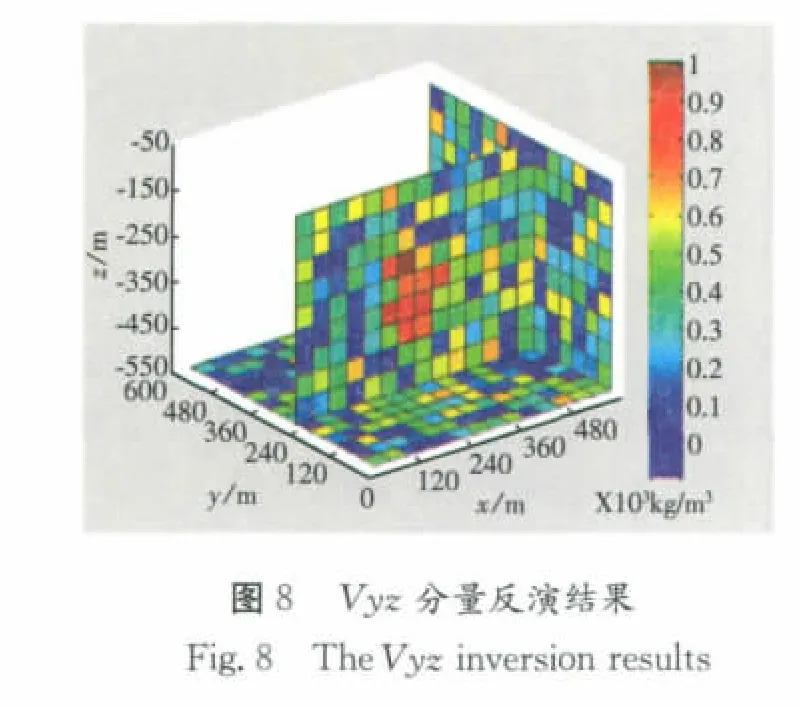
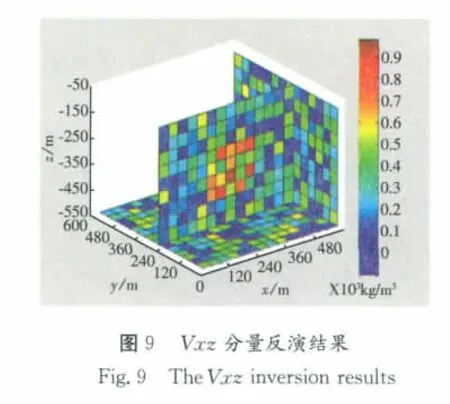
对该目标体分别对各个张量单分量、布格重力异常和全张量进行反演，反演耗时约460s～490s（因初始解是随机设置的，同一张量反演的耗时也会因为初始解设置的差别而略有不同），反演结果见图2至图5、及下页图6～图9，并对比其效果。

从各个分量反演结果图分析可以得到如下结论：

（1）Vxx、Vxy和Vxz分量反演结果都能够大致体现出目标体的范围，但总体上反演得到的密度值偏小，Vxy反演结果在形态上更接近初始模型。

（2）Vyy分量反演的效果较好，在密度值上较接近原始模型，但在形态上比初始模型稍大。

（3）Vyz反演结果物性值分布较集中，值也和初始模型最为接近，但基本上看不出初始模型的分布形态。

（4）Vzz的反演效果最差。

从下页图10分析得到，布格重力异常反演结果能够大致表现出目标体的位置，但密度值略小且不集中。

图11（见下页）为全张量反演结果切片图，可以看出全张量反演结果的密度值要略小，但仍较准确地体现出了异常体的密度，其几何形态特征也与反演模型较接近，目标体所在位置也得到了较好的体现。因此可以认为，全张量反演综合了各个张量分量反演的优点。

4 结语

重力张量各个不同分量在反演过程中表现出对目标体不同敏感度，如目标体埋深、物性参数、目标形态等。而全张量反演能够包含更多的场源信息，相对于单分量反演和布格重力异常反演，其反演结果有着更高的分辨率，且在识别场源特征方面有着更好的表现。

［1］L MARTIN.Advances and challenges in the development and deployment of gravity gradiometer systems［C］.EGM 2007International Workshop：Innovation in EM，Grav and Mag Methods：a new Perspective for Exploration.Capri，Italy，2007.

［2］MURPHY C A.Interpreting FTG gravity data using horizontal Tensor components［C］.EGM 2007International Workshop－Innovation in EM，Grav and Mag methods：new Perspective for Exploration，Ca－pri，Italy，2007.

［3］ALEXANDER DROUJININE，ALEXANDERR VASILEVSKY，RUSS EVANS.Feasibility of using full tensor gradient（FTG）data for detectionof local lateral density contrasts during reservoir monitoring［J］.Geophys，2007 （169）：795.

［4］XIONG LI，MICHEL CHOUTEAU.Three－Dimensional gravity modeling in all space［J］.Surveys in Geophysics，1998，19（4）：339.

［5］HINOJOSA J，K MICHUS.Hilbert transform of gravity gradient profiles：Special cases of the general gravity－gradient tensor in the Fourier transform domain［J］.Geophysics，2002：67.

［6］D W VASCO，C TAYLOR，Inversion of airborne gravity gradient data，southwestern Oklahoma［J］.Geophysics，1991，156（1）：90.

［7］MICHAEL S，ZHDANOV，ROBERT ELLIS，et al.Three－dimensional regularized focusing inversion of gravity gradient tensor component data［J］.Geophysics，2004，69（4）：925.

［8］JULIO CESAR SOARES DE OLIVEIRA LYRIO，LUIS TENORIO，YAOGUO LI，Efficient automatic denoising of gravity gradiometry data［J］.Geophysics，2004，69（3）：772.

［9］JAMES WHILE，ANDREW JACKSON，DIRK SMIT，et al.Spectral analysis of gravity gradiometry profiles［J］.Geophysics，2006，171（1）：11.

［10］KEVIN L.MICKUS，JUAN HOMERO HINOJOSA.The complete gravity gradient tensor derived from the vertical component of gravity：a Fourier transform technique［J］.Journal of Applied Geophysics：2001（46）：159.

［11］GARCIA－ABDESLEM J.Inversion of the power spectrum from gravity anomalies of prismatic bodies［J］.Geophysics，1995（60）：1698.

［12］CHANGYOU ZHANG， MARTIN F， MUSHAYANDEBVU，et al.Euler deconvolution of gravity tensor gradient data［J］.Geophysics，2000，65（2）：512.

［13］余钦范，楼海.水平梯度法提取重磁源边界位置［J］.物探化探计算技术，1994，16（4）：363.

［14］王想，李桐林.Tilt梯度及其水平导数提取重磁源边界位置［J］.地球物理学进展，2004，19（3）：625.

［15］魏伟，刘天佑.梯度法解释复杂二维断裂重力异常［J］.物探与化探，2005，29（8）：347.

［16］赵德军，袁可佳.重力梯度张量计算重力场元［J］.2005，25（6）：12.

［17］李姗姗，吴晓平，吴星.重力矢量及张量信息在地球重力场中的应用［J］.测绘学院学报，2005，22（6）：94.

［18］刘尚余，周方.快速傅里叶变换在卫星重力梯度测量中的应用［J］.华南理工大学学报：自然科学版，1997，25（7）：40.

［19］KENNDY J，EBERHART R C.Particle swarm optimization［C］.Proc IEEE Int Conf on Neural Networks，Perth，W A，Australia，1995.

［20］吴招才，刘天佑.板状体磁异常数据反演的PSO算法［J］.物探与化探，2009，33（2）：194.

［21］邱宁，刘庆生，曾佐勋，等.基于混沌－粒子群优化的磁法数据非线性反演方法［J］.地球物理学进展，2010，25（6）：2150.

［22］FEDI M，FERRANTI L.Florio G，Giori I.Understanding the structural setting in the Southern Apennines（Italy）：insight from Gravity Gradient Tensor［J］.Tectonophysics，2005（397）：21.

［23］曾思红.重力梯度张量正演研究及边界提取［D］.长沙：中南大学，2010.

［24］郭文斌.重力梯度张量的拟BP神经网络反演［D］.长沙：中南大学，2011.

［25］李刚毅，蔡涵鹏.基于粒子群优化算法的波阻抗反演研究［J］.勘探地球物理进展，2008，31（3）：187.