基于OpenCL的显卡加速射线能谱数据处理

刘 端，葛良全，张庆贤，谷 懿

（成都理工大学，成都 610059）

0 前言

现代仪器谱解析，由原来的特征峰解析趋向于全谱解析，多采用矩阵运算实现。因此计算机的数据处理能力和计算时间，是仪器谱解析的重要指标。为了提高仪器谱解析的效率，一般需要对算法进行精简。但是在数学基础上，精简量非常的有限，以矩阵运算的复杂度为例，其精简程度有限［5］而且实际在计算机上的执行效率也不高。另外一种方法，就是提高计算机的计算能力。目前计算机多采用双核或者四核CPU，其数据计算能力大大加强。同时在系统中拥有用于图像处理的GPU，其具有并行计算的特征［3］。但是目前进行核数据处理软件中，多数仍然采用串行单线程为主，没有完全发挥多数据处理器计算机的计算能力。

在计算能力不断提高的计算机系统中，除了传统的计算设备CPU外，其它的设备如GPU、DSP也逐渐进入通用计算行列。由于GPU同CPU相比较，具有其独特的数据并行计算能力，GPU目前已经在科学计算领域扮演着越来越重要的角色。但不同厂家不同型号的设备的差异性，给开发增加了不少难度，由此出现了一些GPGPU开发环境，如OpenCL、CDUA和DirectCompute等，相比于其它两个OpenCL支持设备最为广泛。OpenCL（Open Computing Language，开放运算语言）是一个面向异构系统通用目的并行编程的开放式的免费标准，它规定了一套标准的应用程序接口API，可适用于不同设备［4］。目前常见的如Intel公司的多核CPU、NVIDIA公司的显卡、AMD公司的多核CPU和显卡都可支持［4］。

极大似然估计的仪器谱解析方法是在文献［1］中使用的。极大似然估计方法用来对NaI（Tl）探测的谱线进行解析，通过对合成谱线的解析，说明该方法可以有效地分解能量差为2／3FHWM的重叠峰。但该方法计算量较大，需要经过5 000次以上的迭代计算才能得到结果，对于1 024道的谱线解析将耗时几十分钟，从而不能达到实际应用的目的。作者在本文使用OpenCL在NVIDIA公司的Quadro FX 2700M显卡，以开发并行化的极大似然估计算法为例，提高算法的运行效率，减少算法的执行时间，介绍并行计算在核数据处理中的应用。

1 OpenCL的计算模型构架

OpenCL是面向异构平台的编程标准，将各种计算设备（如CPU、GPU、DSP）组织为统一的平台，并提供完整的并行编程框架。OpenCL程序运行分为Host端与计算设备，Host端程序主要负责管理协调各个不同的计算设备；计算设备上运行的程序称为kernel。通常多个相似的kernel组成一个工作空间，由同一个计算设备并行执行，其中每个kernel称为work－item。每个工作空间由NDRange进行索引（如图1所示），work－item又被分给不同work－group进行管理。同一个work－group中的work－item都由同一个计算单元执行。在同一个work－group中，可以使用其内部高速的loacl memory进行数据共享和线程同步操作，但是不同work－group中的work－item，只能通过速度较慢的global memory共享数据并且不能进行线程同步。

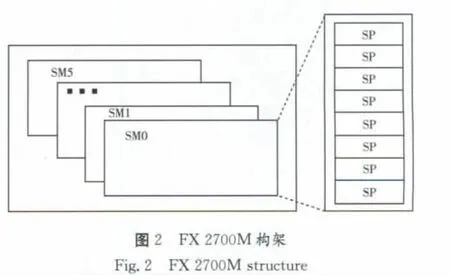
作者在本文使用的是NVIDIA Quadro FX 2700M显卡，其主要计算构架如图2所示，在图2中的SM（Stream Multiprocessor流多处理器），即前文提到的计算单元。该显卡有六个SM，每个SM拥有八个SP（Stream Processor流处理器。OpenCL的work－item运行在SP上，而同一work－group中的work－item运行于同一SM。FX 2700M显卡共拥有四十八个SP（即通常所说的48核），其核心频率为1 350MHz，理论浮点计算能力为190.8GFLOPS（十亿次浮点运算每秒）。

2 计算实现

极大依然法［1］的计算主要是对一方程组采用Richardson－Lucky（R－L）迭代公式进行求解，表达式为：

该计算主要是求式（1）右边的与x相乘的式子的值：

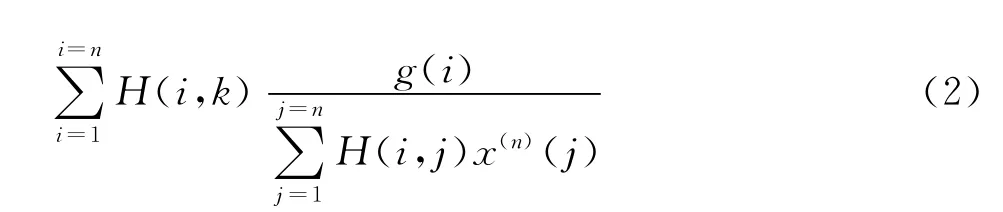
则t（n）（i）＝g（i）／u（n）（i）。

式（2）计算过程如下：

步骤①先求u（n）＝Hx（n）；步骤②再由t（n）（i）＝g（i）／u（n）（i）求t（n）；步骤③再求 HTt（n）得到结果。

此过程中有两次矩阵与向量的乘法运算，此运算的实现是关键。

3 OpenCL内核程序的实现

矩阵与向量乘法式（3）对于每行值的计算，具有计算过程一致、结果相互不影响的特点，因此可以将其并行执行。1 024道的数据可以分给1 024个线程分别进行计算。

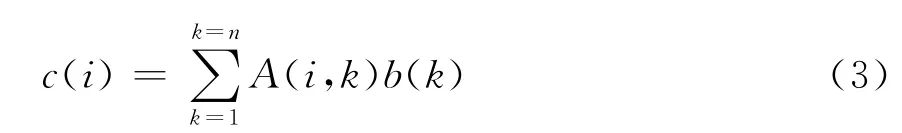
FX 2700M显卡中单个SM虽然拥有八个SP，但对数据的并行访问是十六个work－item一起同时进行。基于对内存访问速度的考虑，最佳的访问方式为每个work－group所含的work－item为十六的整数倍。由于每道的计算都要用到t（n），对于同一work－group内的计算，可将t（n）存入快速的local memory，让同一 work－group内的work－item共享访问以减少数据读入次数。因此应提高每个work－group的work－item拥有量，但是work－group数量减少会影响计算单元的使用效率。作者在本文将1 024个work－item分为十六个work－group，每个work－group含有六十四个work－item。

OpenCL内核kernel程序可以用OpenCL C语言编写。

t（n）的计算代码：

由于要合并访问global memory中数据需要把矩阵H按列存储，可共享的向量x读入快速local memory。

HTt（n）计算代码：

同理，此次需要计算的矩阵为HT需要将其按列存储，即H按行存储。由于H拥有按列存储和按行存储两种模式，所以在计算之前将其分别存储为两个矩阵。

进一步观察H的值发现，其每列数据都是随着离矩阵对角线距离的增加而逐渐减小，在距离大于一定值过后可以忽略不计。矩阵数据集中在矩阵对角线两侧，可将H当作带状矩阵处理，以降低计算量。

4 计算效果比较

本测试机器配置为CPU Intel Core 2T9600 2.8GHz，其理论浮点计算能力为22.4GFLOPS，内存4G，显卡为Quadro FX 2700M，显存512M，理论浮点计算能力为190.8GFLOPS。处理1024道谱线耗时见表1。

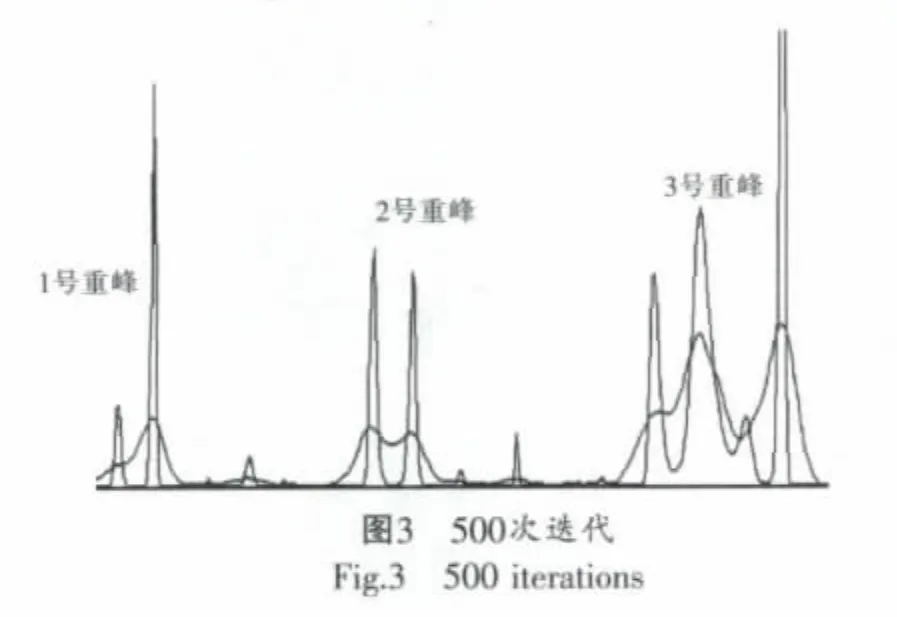
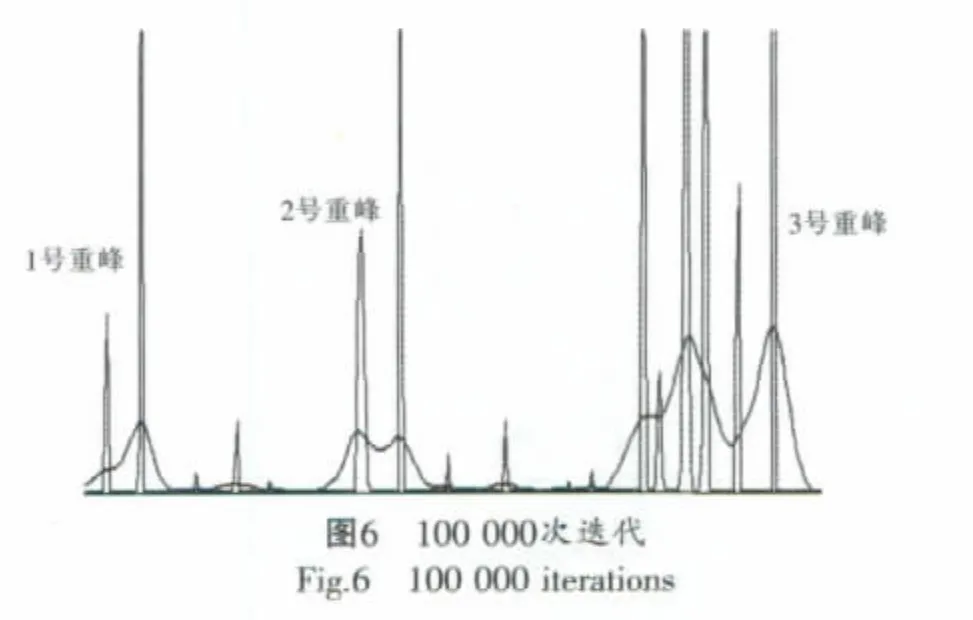
运用该程序对一仪器谱就行处理。谱线总道数为1 024，其中314至634道有三处重峰。见下页，图3至图6是对重峰的分离效果。

由图3至图6可知，1号重峰500次便可分离，2号重峰1 000次就可分离，但是3号要100 000次才可分离，若用CPU程序要耗时近20min，而GPU只用了不到7s。

表1 计算耗时比较（单位：s）Tab.1 Computation time comparison（uint：s）

5 结论

作者在本文通过OpenCL利用GPU的强大的并行计算能力和优化算法，降低了仪器谱全谱解析所耗时间，同单纯的采用CPU计算相比，能够有效地缩短计算时间。对同一谱线测试表明，采用GPU并行计算，其计算时间减少为采用单纯CPU计算的1%。GPU并行计算，对核能谱进行全谱解析具有其自身的优势，增加了该方法的实际可行性。

［1］张庆贤，葛良全，谷懿，等.基于极大似然估计的NaI（Tl）晶体仪器谱解析方法研究［J］.核技术，2011（8）：11.

［2］张庆贤.航空γ能谱特征和仪器谱解析方法研究［D］.成都：成都理工大学，2010.

［3］张舒，褚艳利.GPU高性能运算之CUDA［M］.北京：中国水利水电出版社，2009.

［4］AAFTAB MUNSHI.The OpenCL Specification［M］.Khronos OpenCL Working Group，2011.

［5］COPPERSMITH D，WINOGRAD S.Matrix multiplication via arithmetic progressions［M］.Symbolic Compute，1990.

［6］丁洪林.核辐射探测器［M］.哈尔滨：哈尔滨工程大学出版社，2010.

［7］裴少英，王南萍.航空γ能谱全谱数据的高斯分解方法［J］.科技导报，2006（11）：11.

［8］IAEA.Airborne gamma ray spectrometer surveying［R］.IAEA Technical Reports，2003.

［9］ICRU.International Commission on Radiological U－nits and Measurements［R］.ICRU report 53，Bethesda，Maryland：U.S.A，1994.

［10］DUBOIS G，DE CORT M.Mapping 137Cs deposition：data validation methods and data interpretation［J］.Journal of Environmental Radioactivity，2001，53（3）：271.

［11］李惕碚，吴枚.高能天文中成像和解谱的直接方法［J］.天体物理学报，1993（3）：215.

［12］李惕碚.能不能用低分辨仪器实现高分辨观测［J］.大自然探索，1999（1）：45.

［13］庞巨丰.γ能谱数据分析［M］.西安：陕西科学技术出版社，1993.

［14］王振国.基于极大似然原理的天然图像盲恢复与重建［D］.郑州：解放军信息工程大学，2006.

［15］张贤达.矩阵分析与应用［M］.北京：清华大学出版社，2004.