大直径灌注桩低应变检测中纵波速测不准问题的研究

胡新发，柳建新

（中南大学 地球科学与信息物理工程学院，长沙 410083）

0 前言

反射波法用于基桩的低应变完整性检测，其理论依据是一维波动方程，波在横截面上是同幅值、同相位的。而在实际上，波在桩中的传播是三维的，当力棒在桩头激振时，将产生纵波、横波及瑞利波，其在桩头附近产生多次反射，形成干扰，影响接收波形的质量。为此，前人已做了大量的工作，寻求消除这种干扰的理想途径。如：Liao and Roesset［1、2］通过比较三维模拟的结果与一维的桩顶响应，认为三维效应受频率，特别是高频的影响；陈凡等［3］将桩顶信号的振荡归结为桩顶部的横波和瑞利波的多次反射，认为将传感器安装在离桩轴心2／3R（R为桩的半径）处时，振荡最小，并将这一结论作为传感器安装要求写进了《建筑基桩检测技术规范》（JGJ106－2003）［4］；Chow et al.［5］研 究 认为，要使首波的反相部份最小，传感器与激振点的距离必须大于1／2R ；Seidel and Tan［6、7］研究了消除瑞利波的影响的方法；Chai［8］等认为首波特征波长小于二倍桩径时，桩中的波表现出明显的三维特征；当桩身深度缺陷大于两倍桩径，首波特征波长大于四倍桩径时，传感器位于0.6倍桩半径时，可以简单地用一维波动理论来解释反射波。但前人的这些研究，尚没有涉及三维效应对反射波检测波速的影响。作者在本文通过对纵波波速测不准的原因的研究，提出了考虑时间延滞后的波速计算公式，并用于工程实践，效果显著。

1 纵波波速测不准问题

1.1 两个现场实验

首先列举两个不同桩径、桩长现场实验。

1.1.1 实验一简述

实验对象：永州市冷水滩区珊瑚商住楼A栋3＃桩。

（1）桩参数。

桩型：人工挖孔灌注桩。

桩径：1.0m。

桩长：5.3m。

持力层性质：灰岩，强度标准值61.2MPa。

混凝土强度等级：C25。

龄期：7天。

（2）检测设备及设置。

动测仪型号：RS－1616K（P）。

传感器：为武汉岩海公司生产的高阻尼速度计，灵敏度为230mv／（cm·s－1），两只。

仪器设置：使用其浅层地震菜单，传感器接E1、E2通道，通道触发模式。

传感器布置：两传感器间距约28cm，2＃传感器距桩边17cm。

传感器耦合方式：黄油。

采样间隔：24μs，为仪器该模式下能设置的最小采样间隔。

锤击点：位于桩中心，与1＃传感器相距10cm。激振方式：用尼龙头锤敲击。

现场实验一如图1所示。实测波形见图2。两根曲线的特征数据见下页表1。

由表1可知，两曲线的起跳时间相差0.15ms，计算表面波的波速为1 867m／s。首波峰时相差0.36ms。但桩底反射波波峰时差仅为0.02ms。按首波峰与桩底反射波峰计算，1＃曲线计算桩的纵波波速为：3 323m／s；2＃曲线计算桩的纵波波速为：3 655m／s。由此可见，传感器安装位置影响到计算桩的纵波波速。另外，从波的幅值来看，两只传感器接收到的首波幅值相差近一倍，而桩底反射波幅值相差很小，不足1%。

1.1.2 实验二简述

实验对象：永州市冷水滩区湘江国际景苑50＃桩

（1）桩参数。

桩型：旋挖灌注桩。

桩径：实测桩直径1.30m。

桩长：9.5m。

持力层性质：炭质灰岩，强度标准值为30.7MPa。

混凝土强度等级：C35。

龄期：＞100天。

（2）检测设备及设置。

动测仪型号：RS－1616K（P）。

传感器：为武汉岩海公司生产的高阻尼速度计，灵敏度为230mv／（cm·s－1），两只。

仪器设置：使用其浅层地震菜单，传感器接E1、E2通道，通道触发模式。

传感器布置：两传感器间距约28cm，2＃传感器距桩边为20cm。

传感器耦合方式：黄油。

采样间隔：24μs，为仪器该模式下能设置的最小采样间隔。

锤击点：位于桩中心，与1＃传感器相距17cm。

激振方式：用尼龙头锤敲击。

传感器安装位置及桩中心激振点均已磨平整。

实验现场二如下页图3所示。实测波形见下页图4。两根曲线的特征数据见下页表2。

由表2可知，两曲线的起跳时间相差0.15ms，计算表面波的波速为1 867m／s。首波峰时相差0.32ms。但桩底反射波波峰同时到达。按首波峰与桩底反射波峰计算，1＃曲线计算桩的纵波波速为：3 878m／s；2＃曲线计算桩的纵波波速为：4 166m／s。同样可见，传感器安装位置影响到计算桩的纵波波速。另外，从波的幅值来看，两只传感器接收到的首波幅值相差近一倍，而桩底反射波幅值几乎相同。

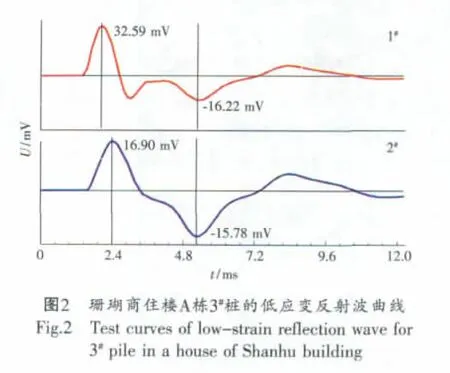
表1 3＃桩的反射波曲线的特征数据Tab.1 The characteristic data of reflection wave curves for 3＃ pile

表2 50＃桩的反射波曲线的特征数据Tab.2 The characteristic data of reflection wave curves for 50＃ pile

1.2 理论分析

在低应变反射波检测中，由手锤或力棒激励产生的类似钟形（高斯曲线）的脉冲，脉冲宽度Tp（时间）约在0.5ms～1ms之间。混凝土的波速c约4 000m／s，脉冲的特征波长为ˉλ＝Tp·c＝（2～4）m，一般比桩的直径（0.8m～1.5m）大。

当力棒作用于桩的中心激发信号时，将产生向四周传播的体波（压缩波和剪切波）及瑞利波。压缩波（P波）、剪切波（S波）及瑞利波（R波）的传播速度分别为［9］：

纵波波速：

横波波速：

表面波波速：

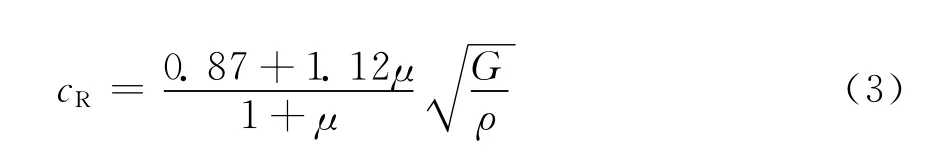
其中 E为混凝土的弹性模量；G为混凝土的剪切模量；μ为混凝土的泊松比，一般可取0.2；ρ为 混凝土的质量密度。

由初始激励所激发的应力波中，瑞利波占有大部份能量，剪切波次之，压缩波所携带的能量最小。各波以敲击点为圆心，以不同的速度传向桩顶面周边过程中，能量都将衰减，但衰减速率以瑞利波最慢。若记敲击点处产生最大峰值的时刻为t0，对于圆形混凝土桩，在距圆心（敲击点）为r的圆周上速度达到最大值的时刻基本满足［9］式（4）。

这样在实际测试中，距圆心敲击点不同的距离r上波的峰值不同，到达的时间有先后。但是，桩底反射回桩顶时刻（2L／c）速度峰值不仅同幅，而且是同一时刻。究其原因是由于桩长比桩径大很多，波被传到桩的下部时，可视波阵面为一平面，当由桩底反射回桩顶时，使桩顶面同时接收反射信号，且幅度相等。

在实际工程桩测试时，锤击点总是与传感器有一定距离，测到的入射速度峰值总比激发点处的速度峰时间滞后。按入射峰－桩底反射峰确定的一维纵波波速比真实的高；反之，若已知正确的波速，则确定的缺陷位置比实际的浅。滞后时间与传感器与激发点间的距离成正比，在大直径灌注桩的检测中，滞后明显。

这种滞后，对检测波速的影响表现在两个方面。

（1）对于相同的桩长，桩径越大，波速偏高越多。如：对于桩长为10m的大直径桩，桩径由0.8m逐渐变化到2.8m，波速由偏高2.46%逐渐变化到偏高9.17%，如图5（a）所示；对于桩长为20m的大直径桩，桩径由0.8m逐渐变化到2.8m，波 速 由 偏 高 1.21% 逐 渐 变 化 到 偏 高4.38%，如图5（b）所示。

（2）对于相同的桩径，桩长越短，波速偏高越多，如：对于桩径为1.0m的大直径桩，桩长由5m逐渐变化到20m，波速由偏高6.38%下降到1.52%，如图6（a）所示；对于桩径为1.5m的大直径桩，桩长由5m逐渐变化到20m，波速由偏高9.89%下降到2.30%，如图6（b）所示。

需指出的是，图5与图6中的偏离是按（JGJ106－2003）规范要求，锤击点位于桩的中心，传感器安放于离桩中心（＝）处（见下页图7），并设定μ＝0.2时计算得到的。

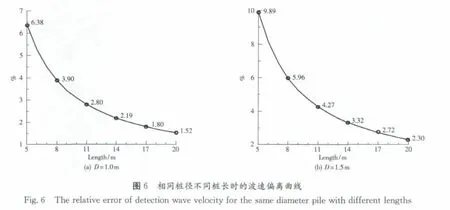
图7 传感器安装点、锤击激振点布置示意图Fig.7 Schematic of the locations of sensor and excitation point

为了消除曲线首波时间滞后引起的速度偏差，需建立考虑时间滞后的纵波波速公式。

2 考虑时间滞后的纵波波速计算公式

2.1 考虑时间滞后的完整桩纵波波速计算公式

取式（2）与式（1）的比值

又由式（2）与式（3）可得式（6）。

将式（5）代入式（6）中得到式（7）。

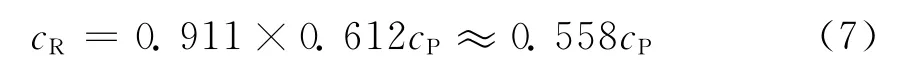
滞后时间可由式（7）求出式（8）。

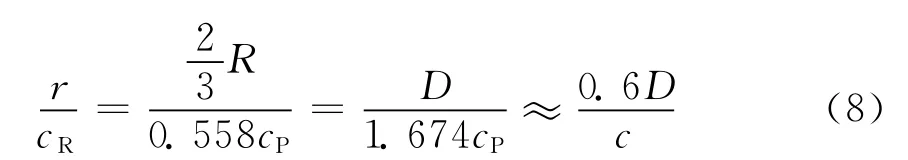
对于完整桩，如下页图8所示。

桩身混凝土纵波波速为

由式（9）可得式（10）。

式（10）即为所求的考虑滞后时间的混凝土纵波波速公式。

进一步，若已知混凝土的纵波波速，桩长可按式（11）计算：

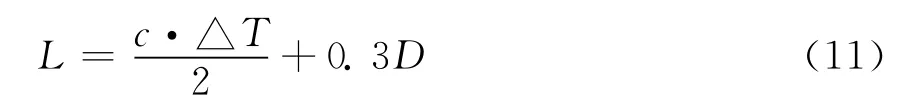
在图8中，△T＝4.810ms，D＝0.8m，按式（10）计算，混凝土的纵波波速为：3 642m／s。按（JGJ106－2003）规范计算的混凝土纵波波速（3 743m／s）比实际波速高了2.8%。

2.2 考虑时间滞后的缺陷位置计算公式

规范JGJ106－2003中桩身缺陷位置采用式（12）计算：

式中 x为桩身缺陷至传感器安装点的距离；△tx为速度波第一峰与缺陷反射波峰间的时间差（见下页图9）；c为受检桩的桩身波速，无法确定时用cm值替代。

如前述，传感器安装点的首波（入射峰）肯定比锤击点处滞后，考虑到表面波（R波）比剪切波（S波）低，比纵波（P波）低得多，特别对大直径桩，这种从锤击点起由近及远的时间线性滞后明显增加。而波从缺陷以一维平面应力波反射回桩顶时，引起桩顶面各点的纵向运动在同一时刻都是相同的，不存在由近及远的时间滞后。所以，按首波波峰与桩底反射波峰确定的波速比实际的高，确定的缺陷位置比实际的浅。

式中 c按式（10）计算。

2.3 桩身下部缺陷平均波速计算公式

对于大直径灌注桩下部易出现混凝土缺陷的情况，当锤击点位于桩的中心，传感器安装在离桩中心2／3半径处时，缺陷段的平均波速cd可用式（14）确定：

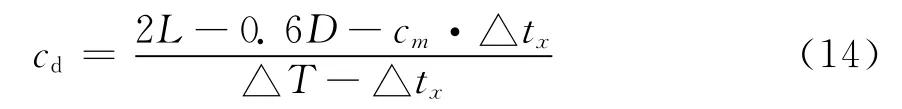
若考虑时间滞后，式（12）修正变为式（13）。

式中 L为桩长（m）；D为桩径（m）；cm为桩身完整段的混凝土波速，可用桩身完整性为Ⅰ类桩的平均波速代替（m／s）；△tx为首波波峰与缺陷反射波峰间的时间差（s）；△T为首波波峰与桩底反射波峰间的时间差（s）。

3 工程实例

零陵学院逸夫楼为框架结构，采用人工挖孔灌注桩基础，地基土地层自上而下为粘性土、白云质灰岩，地下水丰富。桩端持力层为中～微风化白云质灰岩。经动测发现，E－48＃桩桩身存在严重的缺陷，桩底也有强烈的同相反射，存在明显的异常，见图10。该桩桩长为7.20m，桩径为800mm，桩身缺陷反射时间 △t1＝3.05ms，桩底反射时间△t2＝3.87ms，正常Ⅰ类桩混凝土波速为3 880m／s。采用式（14）计算缺陷至桩底段的平均波速cd＝2 544m／s，说明混凝土质量差，缺陷至桩底段的长度计算为1.04m，上部完整段桩长为6.16m。该工程同类型桩的动刚度为1.25×106kN／m～1.60×106kN／m ，但该桩的动刚度仅为5.54×105kN／m，明显低于正常值。经钻芯法验证，芯样照片见下页图11。该桩桩长为7.20m，在6.30m～6.70m之间的芯样松散，缺陷深度与计算值相符，可进一步计算出6.30m～6.70m段的平均波速为1 423m／s，说明混凝土极松散；在7.20m～7.50m之间岩石极破碎，并且泥质充填。该桩的桩身完整性为Ⅳ类，桩端岩石极破碎，持力层性质不满足要求，判定该桩不合格。

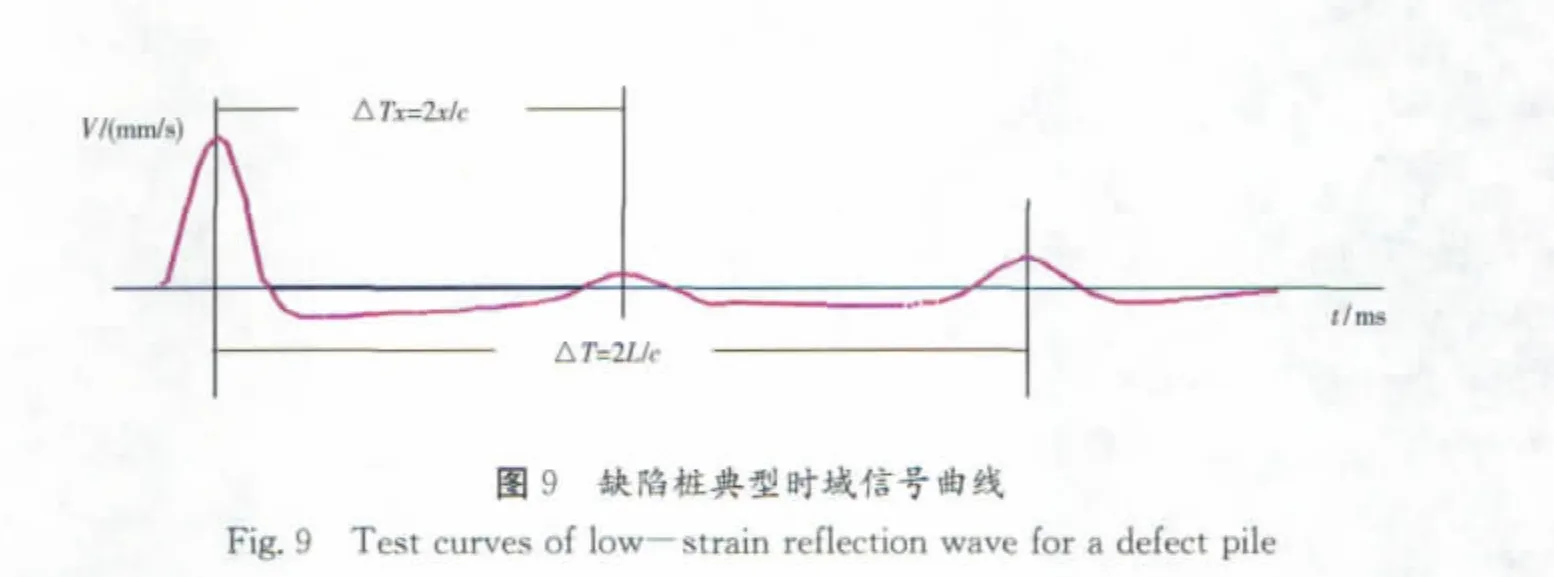
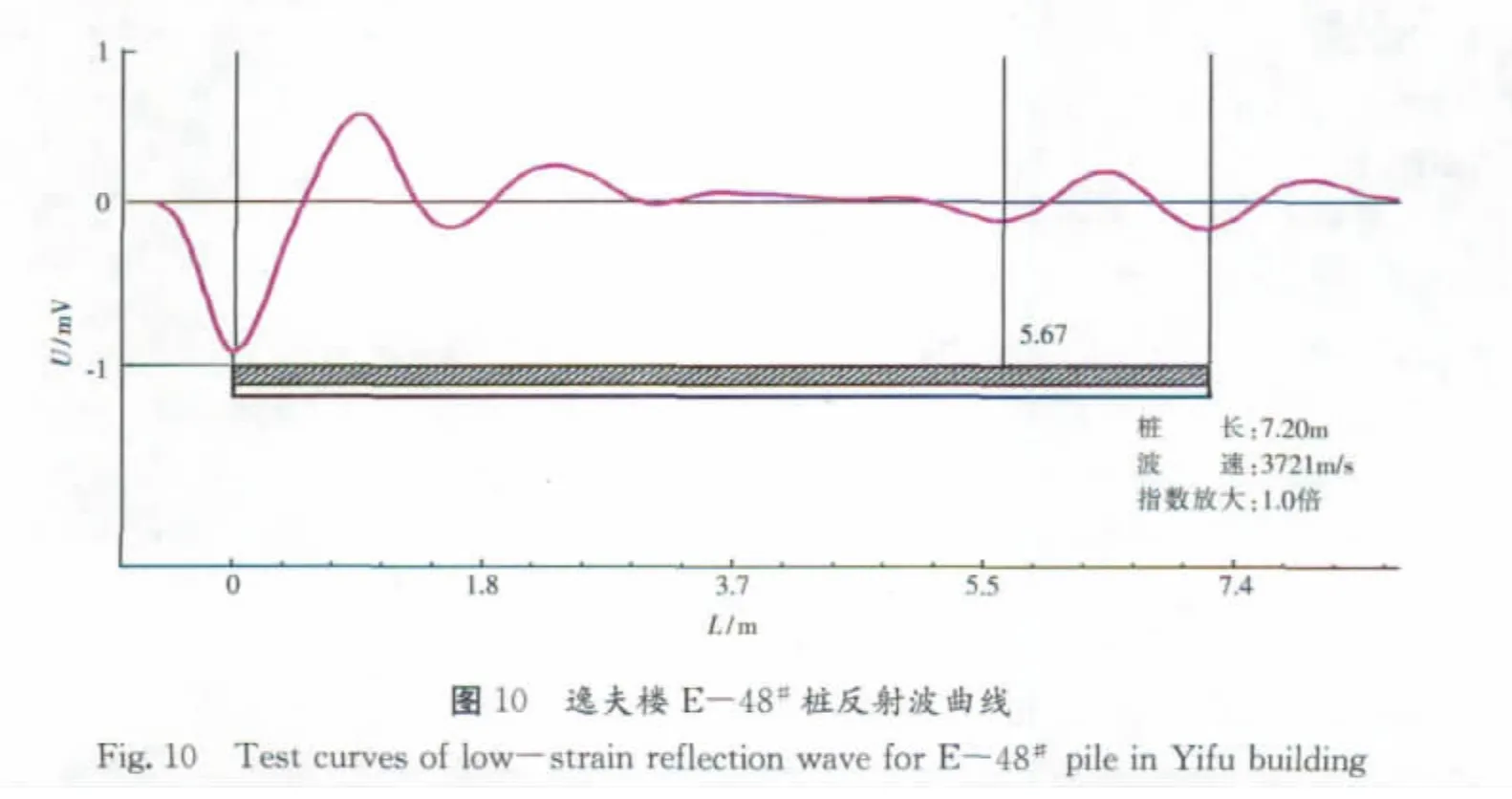
图11 逸夫楼E－48＃桩钻芯检测芯样Fig.11 Core samples for E－48＃pile in Yifu building

如果按规范（JGJ106－2003）给出的公式（12）计算，c为3 721m／s，缺陷位置x为5.67m，与实际位置相差较远。若按缺陷段长度为1.53m，纵波走时按0.82ms计算，缺陷段的平均波速将达3 732m／s，比桩身的平均波速高，明显违背常理。

5 结语

（1）作者在本文通过两个实验，说明了传感器安装位置不同，计算的纵波速不同。分析了大直径桩反射波法检测桩身完整性时纵波波速测不准的原因，即传感器安装点的首波（入射峰）肯定比锤击点处滞后。而波从缺陷以一维平面应力波反射回桩顶时，引起桩顶面各点的纵向运动在同一时刻都是相同的，不存在由近及远的时间滞后。所以，按首波波峰与桩底反射波峰确定的波速比实际的高，确定的缺陷位置比实际的浅。

（2）作者通对分析计算目前检测波速偏离实际波速的程度与桩长、桩径的关系，得到如下结论：①对于相同的桩长，桩径越大，波速偏高越多；②对于相同的桩径，桩长越短，波速偏高越多。

（3）作者提出了考虑时间滞后的桩身纵波波速计算公式、桩身缺陷位置的计算公式，以及桩身下部缺陷段的平均波速计算公式，可用于大直径桩的常规检测和加固效果的检测［10］，经工程实例证实，结果可靠。

（4）在现场检测时，需严格按规范要求布置传感器和激发点。否则，检测波速会出现小的偏差。

（5）采用本文作者提出的计算公式，对基桩检测完整性定量分析也是很有益的，对提高基桩低应变检测水平无疑能起到积极地推动作用。

［1］LIAO S.T，ROESSET J.M.Dynamic response of intact piles to impulse loads.In［J］.J.Numer.Ana－lyt.Meth.Geomech.，1997（21）：255.

［2］LIAO S.T，ROESSET J.M.Identification of defects in piles through dynamic testing［J］.Int.J.Numer.Anal.Methods Geomech.，1997（21）：277.

［3］陈凡，王仁军.尺寸效应对基桩低应变完整性检测的影响［J］.岩土工程学报，1998，20（5）：95.

［4］中华人民共和国行业标准编写组.JGJ 106–2003建筑基桩检测技术规范［S］.北京：中国建筑工业出版社，2003.

［5］CHOW Y.K，PHOON K.K，CHOW W.F，et al.Low strain integrity testing of piles：Three dimensional effects［J］.J.Geotech.Geoenviron.Eng.，2003，129（11）：1057

［6］SEIDEL J.P，TAN S.K.Elimination of the Rayleigh wave effect on low strain integrity test results＿part 1：Experimental investigation［J］.Proc.，7th Int.Conf.on the Application of Stress Wave Theory to Piles，Institution of Engineers Malaysia，Petaling Jeya，Malaysia，2004：179

［7］SEIDEL J.P，TAN S.K.Elimination of the Rayleigh wave effect on low strain integrity test results＿part 2：Rayleigh wave elimination technique［J］.Proc.，7th Int.Conf.on the Application of Stress Wave Theory to Piles，Institution of Engineers Malaysia，Petaling Jeya，Malaysia，2004：187

［8］HUA YOU CHAI，KOK KWANG PHOON，F.ASCE，et al.Effects of the source on wave propagation in pile integrity testing［J］.Journal of Geotechnical and Geoenvironmental Engineering.ASCE，2010，136（9）：1200

［9］陈凡，徐天平，陈久照，等.基桩质量检测技术［M］.北京：中国建筑工业出版社，2003.

［10］胡新发，柳建新.山地和岩溶地区端承桩质量检测与加固技术研究［J］.岩土力学，2011，32（S2）：686.