旋转加速度计重力梯度仪数据处理方法

钱学武　 蔡体菁

(东南大学仪器科学与工程学院, 南京 210096)



旋转加速度计重力梯度仪数据处理方法

钱学武 蔡体菁

(东南大学仪器科学与工程学院, 南京 210096)

为了有效去除旋转加速度计重力梯度仪输出信号中的各种干扰噪声,提出了一种提取重力梯度信号的有效方法．首先对重力梯度仪输出信号进行故障诊断,然后采用基于Chebyshev最佳一致逼近法设计的带通滤波器对故障诊断后的信号进行滤波,并对滤波后的重力梯度信号进行梯度解调,最后采用dmey小波基函数强制阈值方法对解调后的重力梯度信息做进一步去噪处理．在重力梯度半物理仿真平台上进行了仿真试验测试,结果表明,所提方法可以有效降低有用信号均方差,不会造成数据丢失和信号偏移,提高了重力梯度测量精度．

重力梯度仪;旋转加速度计;梯度解调;带通滤波;小波去噪

高精度重力梯度测量对于空间科学、地球科学、地质科学、能源勘探、惯性导航等领域的研究具有重要意义[1-4]．目前,重力梯度仪主要有旋转加速度计重力梯度仪、超导重力梯度仪、冷原子重力梯度仪、静电重力梯度仪,以及基于微机械加工(MEMS)技术的重力梯度仪等,其中旋转加速度计重力梯度仪是目前唯一成功用于机载/船载动基座上的重力梯度测量仪器[5-8]．

旋转加速度计重力梯度仪由多种机械装置组成,加速度计性能、加速度计安装精度、旋转机构稳定性、温控性能、平台稳定性、电路系统稳定性等因素都会对重力梯度信号造成严重影响[9-10],这些因素会使重力梯度仪输出信号包含各种噪声,降低了测量精度,因此研究重力梯度信号处理方法愈显重要．国外学者已对航空重力梯度仪数据处理方法进行了相关研究[11-13],但都是采用基于计算机模拟仿真的处理方法,可信度不高．由于传统数字滤波器具有平滑效应,会对重力梯度信息起到平滑作用,并且无法滤除重力梯度同频带内的噪声,相比而言,小波分析提供了一种自适应时域和频域同时局部化的多分辨率分析方法,可以很好地体现出信号的非平稳特性,为信号处理提供了一种全新途径[14-16]．本文针对重力梯度信号特点,提出了一种基于小波分析的去除重力梯度干扰噪声方法,仿真实验结果表明该处理方法可以有效去除重力梯度信号中的干扰噪声,提高了重力梯度测量精度．

1　重力梯度信号处理方法

在实际重力梯度测量过程中,由于仪器性能和外部环境的干扰,重力梯度仪输出信号中往往含有多种较大幅度干扰噪声,并且存在数据丢失或数据错误等情况．针对重力梯度信号特点,本文提出一种重力梯度信号有效处理方法:首先对重力梯度仪输出信号进行故障诊断处理,消除故障数据点；然后采用数字带通滤波器对故障诊断处理后的重力梯度信号进行滤波处理并进行重力梯度解调；最后采用小波分解方法对含噪重力梯度信息进行去噪处理,得到高精度重力梯度信息．重力梯度信号处理过程如图1所示．

图1　重力梯度信号处理框图

1.1FIR数字带通滤波器

重力梯度信号信噪比非常低,为了去除噪声获得有用信号,需要设计合适的带通滤波器．现有的数字滤波器设计方法中,在保证滤波器所有性能指标满足的前提下,采用Chebyshev最佳一致逼近方法设计的数字滤波器阶数最小．理论上,FIR滤波器的通带带宽越窄,阶数越高,滤波效果越好,但滤波器阶数太高会出现滤波效果不明显,甚至出现滤波不稳定现象．滤波器阶数可根据Kaiser[17]提出的经验公式进行近似估计:

(1)

式中,N为滤波器阶数;过渡带带宽Δf=(ωs-ωp)/(2π),ωp和ωs分别为滤波器通带和阻带截止角频率;δp和δs分别为滤波器通带和阻带的纹波峰值．本文采用Remez算法设计滤波器,根据重力梯度信号特征,并反复进行实验测试验证,最终得到一组滤波效果较好的带通滤波器参数．本文选取的滤波器参数为:中心频率为0.5Hz,通带带宽为0.02Hz,过渡带带宽为0.01Hz,滤波器阶数为800．

1.2重力梯度解调

旋转加速度计重力梯度仪理想输出信号表达式为

Eout=2RKKI[(Γyy-Γxx)sin2ωt+2Γxycos2ωt]

(2)

式中,Eout为重力梯度仪输出信号;R为加速度计质量中心到GGI圆盘中心的距离;K为重力梯度信号放大增益;KI为加速度计标度因数;ω为GGI圆盘旋转角频率;Γyy,Γxx和Γxy分别为相应方向上的重力梯度张量元素．只要对式(2)在2ω频率上进行幅值解调就可以得到重力梯度分量Γyy-Γxx和Γxy,解调公式为

(3)

式中, T为重力梯度仪圆盘旋转周期．

1.3小波去噪

小波分析属于时频分析的一种,它能够同时给出信号的时域和频域特征,有效区分出信号中的突变成分和干扰噪声,从而实现信号分离和降噪．设重力梯度信号为Γ(t),被噪声污染的重力梯度信号为G(t),重力梯度信号模型可表示为

G(t)=Γ(t)+e(t)

(4)

(5)

式中,j,k分别为离散化的缩放因子和平移因子;ψ(t)为小波基函数;ψ*(t)为ψ(t)的共轭．利用式(5)可得到信号G(t)在第j尺度上的小波系数．采用Mallat算法对信号G(t)进行小波分解和信号重构．

重力梯度信号本质上是一种非平稳低频随机信号,经过小波分解后,在某个分解尺度上的小波系数具有较大幅值,而噪声频带比重力梯度信号频带大得多．针对这种情况,在重力梯度数据去噪阶段采用强制阈值去噪方法．该方法仅对某个尺度下的低频系数进行小波变换来重建信号,直接舍弃其他尺度上的系数分量,从而达到信号降噪的目的．在强制阈值滤波过程中,采用dmey小波基函数,这是由于该小波基具有很好的正则性、紧支撑性和平滑性,并且适合重力梯度信号的特点．对重力梯度信号进行10层分解,经过比较相邻层信号与真实信号的变化趋势发现,第6层低频信号与真实信号比较接近,其他层与真实信号相差较大,故选择第6层低频信号作为重力梯度信息的最终处理结果．

2　半物理仿真实验与结果分析

根据旋转加速度计重力梯度仪工作原理,采用高性能计算机、可编程高精度电流源、低噪声电流放大器、低噪声电压放大器、多路切换开关和高精度数字电压表等高精密仪器组建了重力梯度半物理仿真系统[18]．利用该仿真系统可以完成信号产生、信号放大、信号滤波、重力梯度解调等仿真实验．仿真系统采用LabVIEW软件开发．重力梯度半物理仿真系统实物图如图2所示．

图2　重力梯度半物理仿真系统实物图

采用高密度的钨合金均质圆球作为重力梯度引力装置,利用所开发的重力梯度半物理仿真系统对重力梯度信号进行仿真测试. 实验参数如下:圆球密度为18 000kg/m3,质量为1 000kg,圆球质心坐标为(0.8,0,0)m,圆盘旋转周期为4s,加速度计对的基线距离为0.2m,加速度计标度因数为10mA/g,信号放大增益为5×106,信号采样频率为10Hz．根据万有引力定律，可以计算出在上述参数下圆球引起的重力梯度分量理论值分别为Γyy-Γxx=-393E,Γxy=0E．将从旋转加速度计重力梯度仪样机上采集到的原始加速度计数据作为重力梯度半物理仿真系统信号源,对重力梯度半物理仿真系统输出信号进行数据采集和数据故障诊断处理,然后采用带通滤波器对故障诊断后的重力梯度信号进行滤波．滤波前后的重力梯度信号时域波形如图3所示,对应的频谱如图4所示．

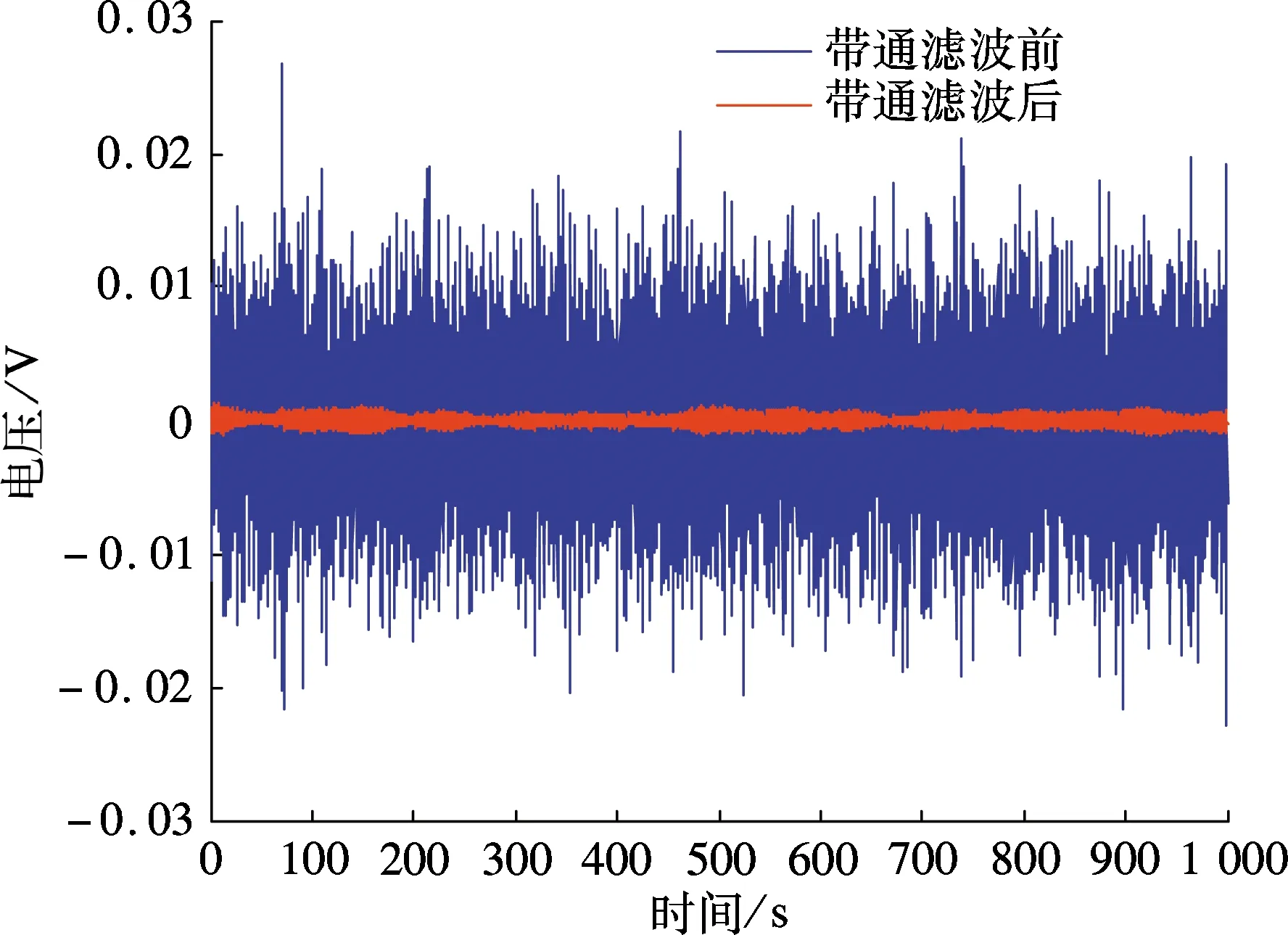
图3　重力梯度信号滤波前后信号波形

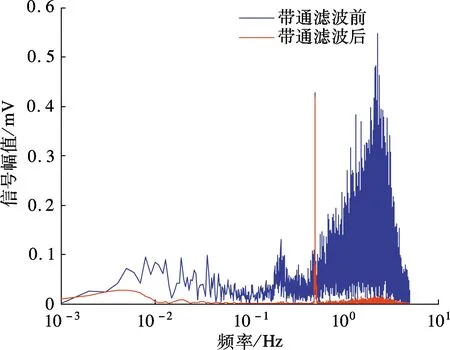
图4　重力梯度信号滤波前后信号频谱

从图3可看出,重力梯度信号全部被噪声淹没,完全看不到重力梯度信号,滤波后的信号幅值大幅降低．从图4可看出,0.5Hz的重力梯度信号较为明显,除0.5Hz外的低高频干扰谐波幅度较大,而带通滤波后的重力梯度信号频谱只含有0.5Hz窄带信号和通带带宽内残留的少量噪声信号,0.5Hz外的高幅值低高频噪声基本被滤除．利用式(3)对带通滤波后的重力梯度信号进行梯度解调,然后对解调得到的重力梯度信息进行100s平滑滤波、200s平滑滤波和小波强制阈值去噪处理,不同处理方法的结果如表1所示,波形对比如图5所示．

从表1和图5可看出,采用平滑滤波处理方法

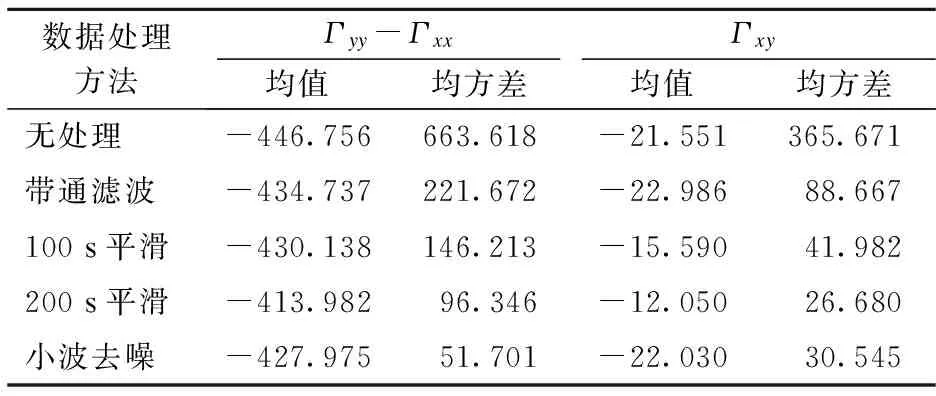
表1　重力梯度不同处理方法结果对比　E

(b) 重力梯度分量Γxy

虽然可以有效去除噪声,但随着平滑时间的延长,重力梯度信息丢失越多,且平滑滤波后的均值发生了明显偏移．而采用小波去噪方法不会出现数据丢失和均值偏移现象,并且可以明显降低重力梯度信息均方差．同时还发现,重力梯度分量Γyy- Γxx和Γxy均值分别约为-430和-22E,而理论值分别为-393和0E,重力梯度测量值与理论值相差较大,这主要是由于在0.5Hz上存在信号串扰.造成信号串扰的原因很多,可通过采用重力梯度标定方法进行重力梯度补偿解决．

3　结语

本文针对重力梯度信号特点,提出了一种去除重力梯度干扰噪声的有效处理方法.首先对重力梯度信号进行故障诊断处理,然后采用带通滤波器对故障诊断后的信号进行滤波,此滤波方法可以把重力梯度信号频率外的低高频干扰噪声滤除,提高了重力梯度信号信噪比;接着对滤波后的重力梯度信号进行梯度解调;最后采用小波去噪方法对解调结果做进一步处理．为了验证所提处理方法的有效性,在重力梯度半物理仿真系统上进行了仿真实验测试．仿真结果表明,小波去噪方法可以显著提高重力梯度测量精度,并且不会造成数据丢失和信号偏移,为实现高精度重力梯度测量提供了一种方法．

References)

[1]Difrancesco D. Advances and challenges in the development and deployment of gravity gradiometer systems[C/OL]//EGM2007InternationalWorkshop. Capri, Italy, 2007. http://www.earthdoc.org/publication/publicationdetails/?publication=41199.

[2]Roberts D, Chowdhury P R, Lowe S J, et al. Airborne gravity gradiometer surveying of petroleum systems under Lake Tanganyika, Tanzania[C]//ASEG-PESA2015. Perth, Australia, 2015:1-5. DOI:10.1071/aseg2015ab161.

[3]Christensen A N, Galder C V, Dransfield M. Improved resolution of fixed-wing airborne gravity gradiometer surveys[C]//2014SEGAnnualMeeting. Denver, Colorado, USA, 2014: 1319-1323. DOI: 10.1190/segam2014-0713.1.

[4]DiFrancesco D, Meyer T, Christensen A, et al. Gravity gradiometry—Today and tomorrow[C]//11thSAGABiennialTechnicalMeetingandExhibition. Swaziland, 2009: 80-83.

[5]Hodges G, Dransfield M H, Shei T C. The Falcon airborne gravity gradiometer for engineering applications[C]//SymposiumontheApplicationofGeophysicstoEngineeringandEnvironmentalProblems2010. Keystone, Colorado, USA, 2010: 443-447. DOI:10.4133/1.3445467.

[6]Christensen A N, Hodges G. HeliFALCON®airborne gravity gradiometer data acquisition in rugged terrain[C]//Proceedingsofthe11thSEGJInternationalSymposium. Yokohama, Japan, 2013:140-145. DOI:10.1190/segj112013-036.

[7]Difrancesco D, Grierson A, Kaputa D, et al. Gravity gradiometer systems—Advances and challenges[J].GeophysicalProspecting, 2009, 57(4): 615-623.

[8]Dransfield M H, Christensen A N. Performance of airborne gravity gradiometers[J].TheLeadingEdge, 2013, 32(8):908-922. DOI:10.1190/tle32080908.1.

[9]Jekeli C. The gravity gradiometer survey system (GGSS)[J].EosTransactionsAmericanGeophysicalUnion, 1988, 69(8):105, 116-117.

[10]Jekeli C. Statistical analysis of moving-base gravimetry and gravity gradiometry[R]. Columbus,Ohio,USA: Geodetic and GeoInfomation Science, The Ohio State University, 2003.

[11]Cesar J, Lyrio S O. Wavelet denoising of gravity gradiometry data[C]//SEGInternationalExpositionand71stAnnualMeeting. San Antonio, USA, 2001:1474-1477. DOI:10.1190/1.1816384.

[12]Carlos D U, Braga M A, Galbiatti H F, et al. Airborne gravity gradiometry-data processing and interpretation [J].RevistaBrasileiraDeGeofǐsica, 2013, 31(3):427-453.

[13]Christensen A N, Dransfield M H, Galder C V. Noise and repeatability of airborne gravity gradiometry [J].FirstBreak, 2015, 33:55-63.

[14]Barnes G, Lumley J. Processing gravity gradient data [J].Geophysics, 2011, 76(2):133-147.

[15]Jekeli C, Abt T L. The statistical performance of the matched filter for anomaly detection using gravity gradients[R]. Columbus, Ohio, USA: Division of Geodetic Science, Ohio State University, 2010.

[16]de Oliveira Lyrio J C S, Tenorio L, Li Y, et al. Efficient automatic denoising of gravity gradiometry data[J].Geophysics, 2004, 69(3):772-782. DOI:10.1190/1.1759463.

[17]Kaiser J F. Nonrecursive digital filter design using the Io-sinh window function[C]//IEEEInternationalSymposiumonCircuits&Systems. San Francisco, CA, USA, 1974:20-23.

[18]蔡体菁,钱学武,丁昊.旋转加速度计重力梯度仪重力梯度信号仿真[J].物探与化探,2015,39(S1):76-79.

Cai Tijing, Qian Xuewu, Ding Hao. Signal simulation of gravity gradiometer of rotating accelerometer[J].GeophysicalandGeochemicalExploration, 2015, 39(S1):76-79. (in Chinese)

DOI:10.3969/j.issn.1001-0505.2016.04.007

Data processing method for rotating accelerometer gravity gradiometer

Qian Xuewu Cai Tijing

(School of Instrument Science and Engineering, Southeast University, Nanjing 210096, China)

In order to remove the noise in the output signals of the rotating accelerometer gravity gradiometer instrument (GGI), an effective method for extracting the gravity gradient signal is presented. First, the fault diagnosis is carried out to preprocess the output signals of the GGI. Then a band-passing filter based on the Chebyshev optimal uniform approximation method is used to filtrate the diagnosed signals, and the output signals of the band-pass filter are demodulated in the next step. Finally, the gravity gradient is further denoised by the compulsory threshold method based on the demy wavelet function. The proposed method is tested on the gravity gradient hard-in-the-loop simulation platform. The simulation results show that the method can effectively reduce the mean square deviation of the useful signals and avoid data loss or signal offset. Therefore, the method can improve the precision of the gravity gradiometer.

gravity gradiometer; rotating accelerometer; gradient demodulation; band-passing filtering; wavelet de-noising

10.3969/j.issn.1001-0505.2016.04.006

2015-12-28.作者简介: 钱学武(1981—)，男，博士生；蔡体菁(联系人)，男，博士，教授，博士生导师，caitij@seu.edu.cn.

国家高技术研究发展计划(863计划)资助项目(2011AA060501).

10.3969/j.issn.1001-0505.2016.04.006.

U666.1

A

1001-0505(2016)04-0708-05

引用本文: 钱学武,蔡体菁.旋转加速度计重力梯度仪数据处理方法[J].东南大学学报(自然科学版),2016,46(4):708-712.