高斯公式在农林院校大学物理保守场中的推算
贾国荣
(山西农业大学 文理学院,山西 太谷030801)
数学是创立和发展物理学理论的主要工具,它的高度抽象性,使它能够概括物理世界的基本结构[1]。数学中的高斯公式是分析大学物理中矢场问题的重要工具[2]。电场中的高斯定理人人皆知,被广泛应用到求解具有高对称性的带电系周围的电场问题中[3],而与电场同属于保守场的万有引力场[4],其中,高斯定理在农林院校大学物理课程中并未提及。由此,本文从数学中高斯公式和保守场的定义谈起,推导出农林类大学物理中两个保守场:电场和万有引力场。把高斯公式推广到电场和万有引力场中,得出各自场中的高斯定理,并分别举例说明高斯定理的运用。
1 数学中高斯公式
高斯公式是数学中曲面积分的一个重要公式,它可以把高斯面上的第二型曲面积分转化为所围体的三重积分[5]。描述为:
设空间区域V的边界曲面S是光滑的或分片光滑的,函数 P(x,y,z),Q(x,y,z),R(x,y,z),在Q及S上具有一阶连续偏导数,S的方向为外法向,则
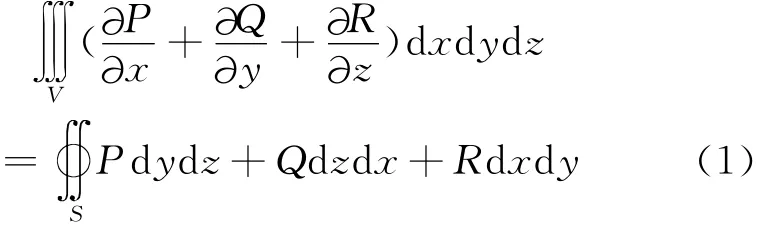
或

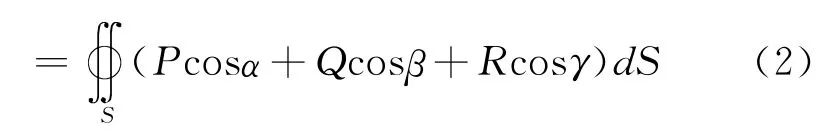
如果引入矢量函数,高斯公式又写为:

数学意义为:矢量场通过闭合曲面S的流量等于此闭合曲面所围体V上每一点的散度在体V上的三重积分。
2 保守场的推导
数学中,保守场的定义为:在矢量场α中,若曲线积分与路径无关,只与起点和终点有关,这种场称为保守场。矢量场α为保守场的充要条件是:▽×α=0
农林院校大学物理课程中,电场力做功和万有引力做功都与路径无关,即:
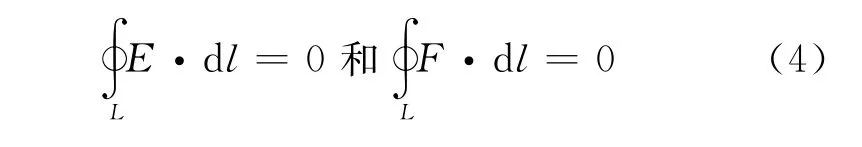
根据斯托克斯定理

得出:

由此从数学推导,可以知道电场和万有引力场都是保守场。
3 高斯公式在电场中的运用
把高斯公式运用到大学物理的电场中,就是电场高斯定理。电场通量(即:闭合曲面所围体V上每一点的散度在体V上的三重积分(即:为电荷体密度[4])。
它可以表述为:通过一个任意闭合曲面S的电通量Φe等于该面所包围的所有电量的代数和∑q除以ε0,与闭合面外的电荷无关。即:

在求解具有高对称性带电体系的电场分布时,电场高斯定理可以大大简化计算过程[6],还反映出电场的另一重要性质:静电场是有源场。正电荷是静电场的源头,向四周辐射电场。
例:求一个均匀带正电球体内外的电场强度分布,设球体带电总量为Q,球体半径为R,如图1。
如果用电场强度叠加原理,把带电体系分割成无穷多个电荷元,其中每个电荷元视为点电荷,对无穷多个电荷元产生的电场积分求和,势必涉及一个三重积分,显然,这在数学计算中是比较复杂的。
如果应用高斯定理,由于电荷Q均匀分布在球面上,其电场分布具有球对称性。在任何与带电球面同心的球壳上的各点,电场强度大小均应相等,方向沿各自的矢径方向。

图1 带电量为Q的球体 (虚线为高斯面)Fig.1 The Sphere Charged of Q(The Dotted Line for Gaussian Surface)
在球面外任取一点P,设想过P点做一个半径为r(r>R)的球面,称之为高斯面,因球面上各点的法线方向与场强方向一致,所以通过该球面的电通量为:
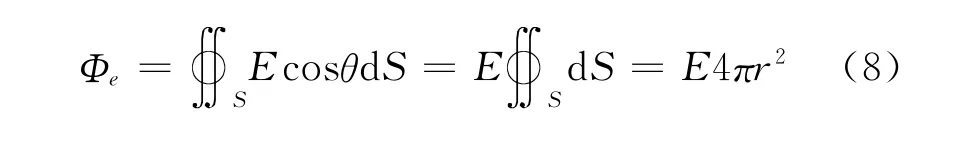
此时,该球面包围的电荷为:

根据高斯定理可得:
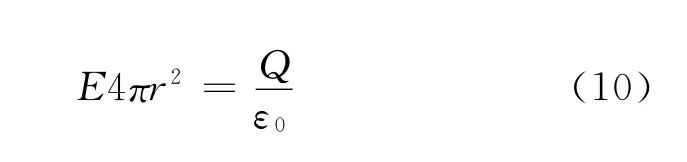
P点的电场强度为

对于球内任一点P′,同样过P′作一半径为r(r<R)的球形高斯面,通过该球面的电通量为:
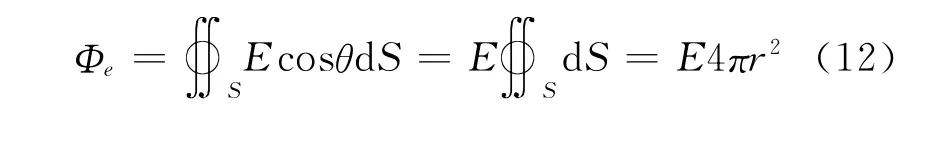
此时,该球面包围包围的电荷为:

由高斯定理可得:

此时必有:

4 高斯公式在万有引力场中的应用
万有引力场和静电场同属于保守场,可以设想万有引力场如同电场一样,是一种物理客观存在。质量为M的物体向四周辐射万有引力场,且万有引力定律F=GM1M2/r2与库仑定律F=Q1Q2/4πε0r2相似,都服从平方反比定律。其中,G和1/4πε0类似,为常数;质量M 和电量Q 类似。运用类比思想[7],把高斯公式应用到万有引力场得,万有引力场通量(Φf=∯SEg·d S),等于闭合曲面所围体V上每一点的散度在体V上的三重积分(-4πG∭ρd v,ρ为质量密度)。它可以表述为[8]:通过一个任意闭合曲面S的万有引力场通量Φf等于该面所包围的所有质量的代数和∑imi除以a0,负号表明万有引力场为汇聚场,穿入闭合曲面S。

电场高斯定理在求解具有高对称性带电体系的电场分布时有着十分重要的地位,同理,在求解具有高对称性质量体系的万有引力场分布时,用万有引力场中的高斯定理会大大简化求解过程[9]。
例:求均质细棒中垂面上的受到的引力场强度,设棒长为2l,如图2。

图2 质量均匀的细棒(圆柱体为高斯面)Fig.2 The Thin Rods With Unifor m Quality(The Cylinder for Gaussian Surface)
如果用万有引力定律计算,选细棒中点O为原点,取坐标轴z沿细棒向上,由于细棒具有轴对称性,取纸平面作代表[10],细棒的中垂面与纸面的交线为中垂线OP。
整个细棒可以分割成一对一对的线元,其中每对线元dz和dz′对于中垂线OP 对称,这一对线质元在中垂线上任一点P所产生的元引力场d Eg和d Eg′也对中垂线对称。他们在垂直于OP方向的分量互相抵消,从而合成矢量d Eg+d Eg′沿中垂线方向其大小为2d Egcosα,其中:

r表示距离OP,λ表示线质量密度,则λd z是总质量。
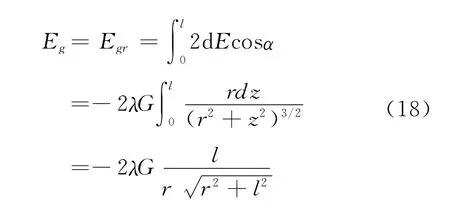
当细棒为无限长时,l→∞,这时的万有引力场强为:

如果用应用万有引力场中高斯定理,因该体系具有轴对称性,若以细棒为轴,在垂直于轴的平面内,同一圆周上的万有引力场大小处处相等,方向垂直于棒,向内汇聚。于是可选取以棒为轴,半径为r,长为l的封闭圆柱面为高斯面。圆柱的上、下两个底面,Eg与d S的方向垂直;侧面的Eg与d S的方向相反,所以通过封闭圆柱体的万有引力通量为:

根据高斯定理得:

得:
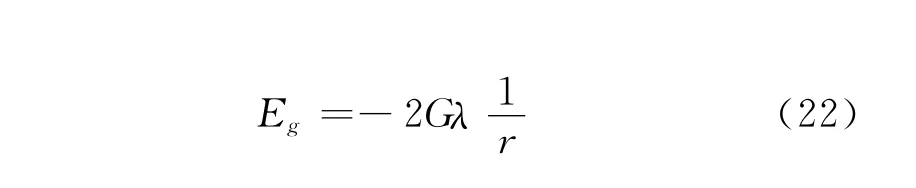
公式(19)与公式(22)是相等的,可以看出,比起用万用引力定律来说,用万有引力高斯定理求解问题比较简单,省去了很多积分过程,并且体现出万有引力场是保守场的性质。
5 结论
运用数学中保守场定义,推导出农林院校大学物理中两个保守场:电场和万有引力场,把高斯公式运用到这两个保守场中,得到人们比较熟悉的电场中的高斯定理,同时,把高斯公式运用到万有引力场中,结合类比思想,得到万有引力场中的高斯定理:

把万有引力场高斯定理运用到实际解题过程中,可以大大简化运算过程,用很好的运用价值。同时,也揭示了万有引力场如同电场一样,是有源场,质量为M的体系辐射万有引力场。
[1]陈修芳.从高斯公式到高斯定理[J].科学之友,2010,5:11-13.
[2]籍延坤.高斯定理的数学证明[J].大连铁道学院学报,2004,25(3)13-16.
[3]温耐,王伟峰.高斯定理在静电场中的应用问题[J].物理通报,2010(11):9-11.
[4]宋克慧,龙文海.关于保守场判据的一点注记[J].蒙自师专学报:自然科学版,1993,10(2):51-53.
[5]四川大学数学系高等数学教研室.高等数学[M].北京,高等教育出版社,1996:234-240.
[6]武秀荣,杨学工.大学物理[M].北京:中国农业出版社,2009:97-102.
[7]蔡香民.万有引力与高斯定理——类比在物理学中的作用[J].安徽师范大学学报:自然科学版,2006,25(2):147-150.
[8]陈学文,李彦敏.万有引力场强度与万有引力场的高斯定理[J].商丘师范学院学报:自然科学版,2005,2(5):161-163.
[9]陈国云,骆成洪,辛勇,等.高斯定理和环路定理在万有引力场中的推广[J].南昌大学学报:工科版,2008(12):354-358.
[10]赵凯华,陈熙谋.电磁学[M].北京:高等教育出版社,2003:13-16.

