玩转三角板——中考复习研讨“K字型全等到相似”的遐想

●

(柯城区石梁镇中学 浙江衢州 324000)

玩转三角板——中考复习研讨“K字型全等到相似”的遐想

●余利英

(柯城区石梁镇中学 浙江衢州 324000)

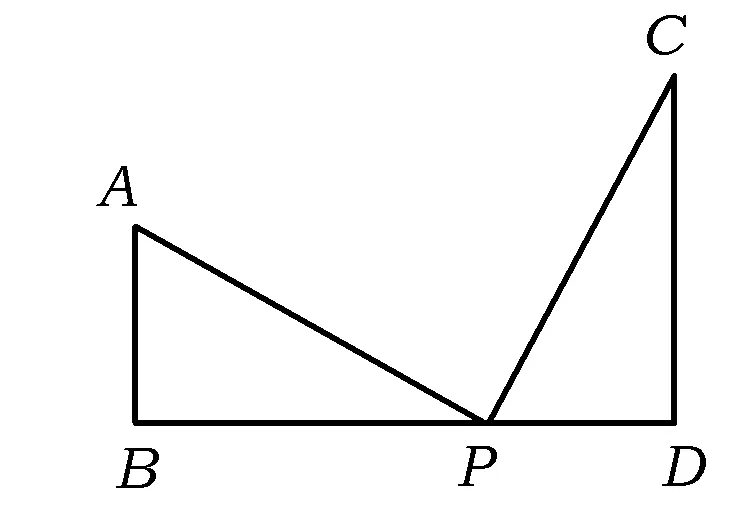
图1

浙教版八年级教材《数学》上册有一道习题如下：

题目如图1，AB⊥BD于点B，CD⊥BD于点D，P是BD上一点，且AP=PC，AP⊥PC,则△ABP≌△PDC，请说明理由.

2013年1月，浙江省衢州市的中考复习研讨课“一组直角三角形”以该题为起点，逐步展开并揭示出问题的基本图形—K字型基本图形.在中考第一轮复习课中，教师应从课本习题出发，让学生明白在中考复习中不能脱离课本，要重视课本中的例题和习题，并进行适当的变式拓展，以提高复习功效.

纵观历年中考，试题中出现的基本模型常与全等三角形、相似三角形、函数等知识相结合.这类试题能很好地考查学生分析、探究问题的能力，因而备受命题者的青睐，常将其设计成填空、选择、解答题.笔者从自身的教学经验出发，对这类问题进行了以下思考.

1 加强动手操作，构建基本模型

K字型全等三角形基本图形构成的条件是3组相等的角，1组相等的对应边，最终是引领学生得到的是其余2组对应边相等.条件与结论都非常简单，关键是如何让学生从复杂的题目背景下抽象出这类基本模型.因为学生都备有三角板、直尺等学具，这道课本习题可以用三角板来演示，让学生在动手操作中发现、并解决问题.操作学具既可以把抽象的知识变成眼前形象的几何图形，又可以很好地发展学生的思维能力，让学生深切感受到这个基本模型原来就在自己的手上.

例1如图2，把45°三角板直角顶点始终放在直尺的边上，如果转动这个三角板，哪些角的大小发生变化？这些变化的角之间是否存在等量关系？如果存在，请指出并说明理由.

设计意图学生直接动手操作，转动三角板，容易发现顶点C处的2个锐角大小改变，但始终保持互余的关系.发现并理解这一结论，为后面证明K字型全等奠定了坚实的基础.

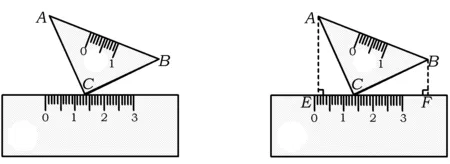
图2 图3

例2如图3，当45°的直角三角板的直角顶点在直尺边上时，如果过直角三角板的斜边的2个端点向直尺边所在的直线作垂线段，当转动三角板时，图3中有哪些线段的长度发生变化？在这些长度发生变化的线段中是否存在长度相等的线段？如果存在，请指出并说明理由.

设计意图发现图1中互余的2个角，为在长度发生变化的线段中寻找相等线段提供了方向，因为它们是K字型全等三角形的对应角.而说明理由的过程，就是对K字型全等三角形的一个认识过程.

揭示课题K字型全等三角形，从中抽象出K字型基本图形(横向的英文字母K)，如图4所示.

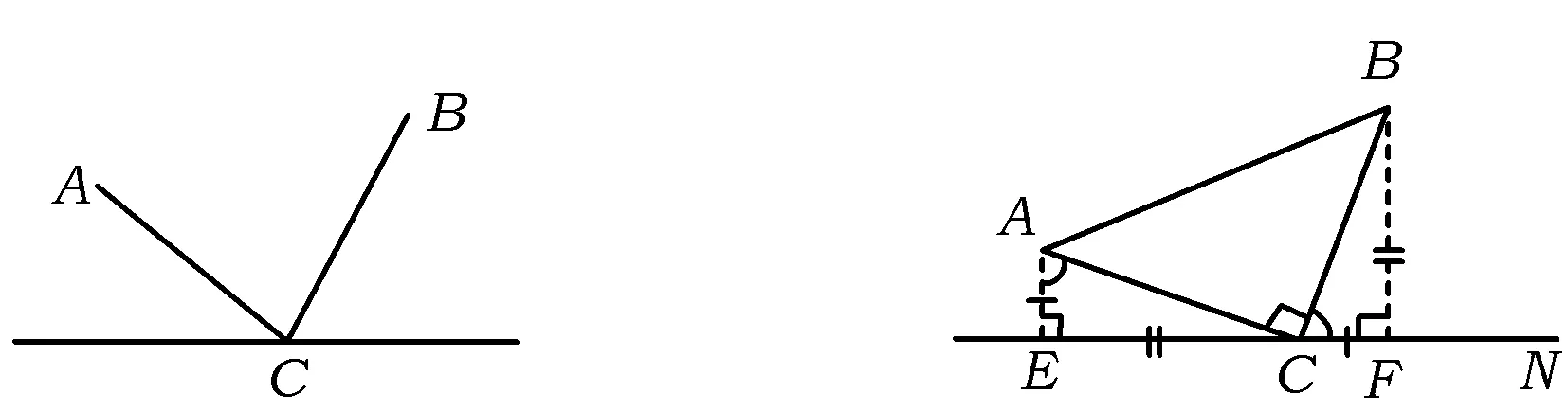
图4 图5

2 K字型全等

2.1 K字型全等图形的识记

条件如图5，∠AEC=∠ACB=∠BFC=90°,且这3个直角都在同一直线上；AC=BC.

结论△ACE≌△BCF，从而EC=BF，AE=CF.

练习1如图6，已知在△ABC中，∠ABC=90°，AB=BC，三角形的顶点在相互平行的3条直线l1，l2，l3上，且l1和l2之间的距离为2，l2和l3之间的距离为3，则AC的长是______，点B到边AC的距离是______.

(2009年浙江省丽水市数学中考试题)

图6 图7

设计意图如图7，因为∠ABC的直角顶点B在直线l3上，所以过点A,C向直线l3作垂线段，即可构造K字型全等基本图形，从而得到△ADB≌△EBC,故DB=CE=5,再利用勾股定理，问题得以解决.

2.2 K字型全等基本图形的变式

(1)变式1：中间的等腰直角三角形变换为正方形，如图8所示.

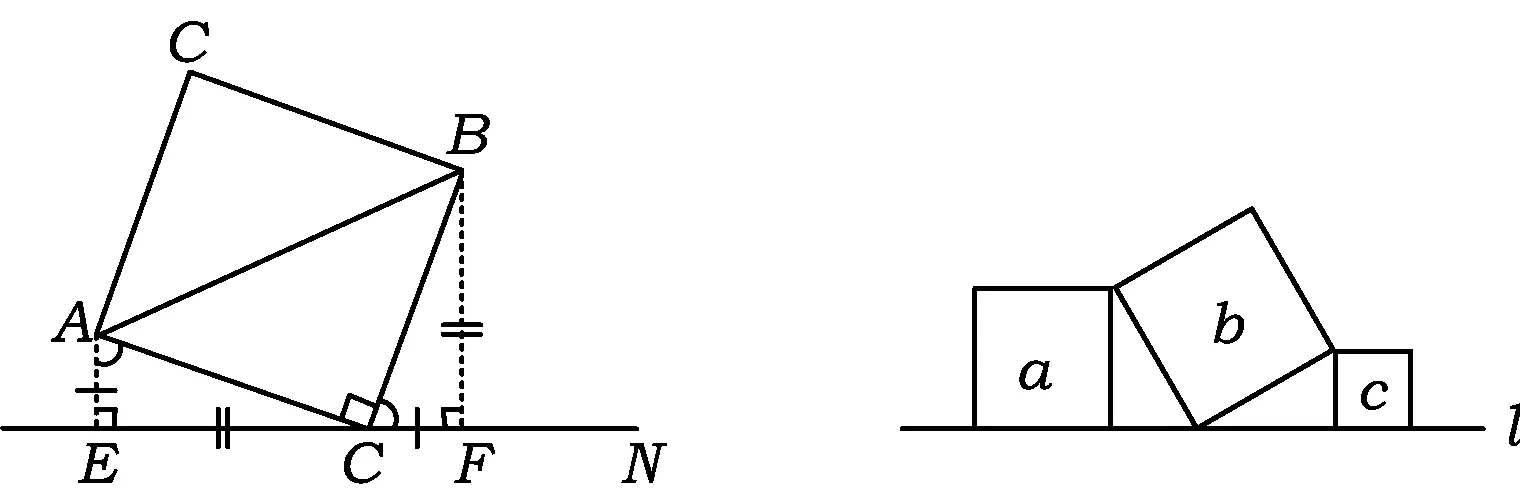
图8 图9

练习2如图9，直线l上有3个正方形a,b,c，若a,c的面积分别是5和11，则b的面积是______.

(2007年江苏省连云港市数学中考试题)

设计意图K字型基本图形处于中间位置的三角形可以是等腰直角三角形，也可以是正方形，它们的作用都是为2侧直角三角形全等提供了直角和一组相等的斜边.因此只要具备同一直线上的3个直角及一组相等的对应边，就能得到K字型全等基本图形.可见，从中找到K字型全等三角形是解答此题的关键.

(2)变式2：置K字型全等基本图形于直角坐标系中.

分析虽然∠ACB的直角顶点C在直线CN上，直接过点A,B向CN作垂线段构成K字型全等的基本图形(如图11)，不利于求点B的坐标.若先过点C作直线CL平行于x轴，再过点A,B作直线CL的垂线段(如图12)，构成K字型基本图形，对应边AK=CL,KC=BL，则与点A,B,C的坐标联系起来.又已知点A,B的坐标，构造如图12所示的K字型全等图形，很容易求出第3个顶点C的坐标.

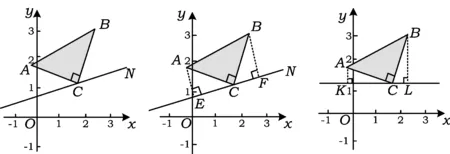
图10 图11 图12

设计意图把K字型基本图形放置于直角坐标系中，已知等腰直角三角形2个顶点的坐标，就可以求出第3个顶点的坐标.值得注意的是一线3个直角中的“一线”尽可能是水平线或竖直线，这样构建K字型全等图形后，联合三角形的顶点坐标，列方程求解即可.

练习题3如图13，已知在矩形ABCO中，O为坐标原点，点B的坐标为(8，6)，点A,C分别在坐标轴上，P是线段BC上的动点.设PC=m,点D在第一象限，且是直线y=2x+6，y=2x-6中某条直线上的一点.若△APD为等腰直角三角形，则点D的坐标为______.

(2010年浙江省义乌市数学中考试题)

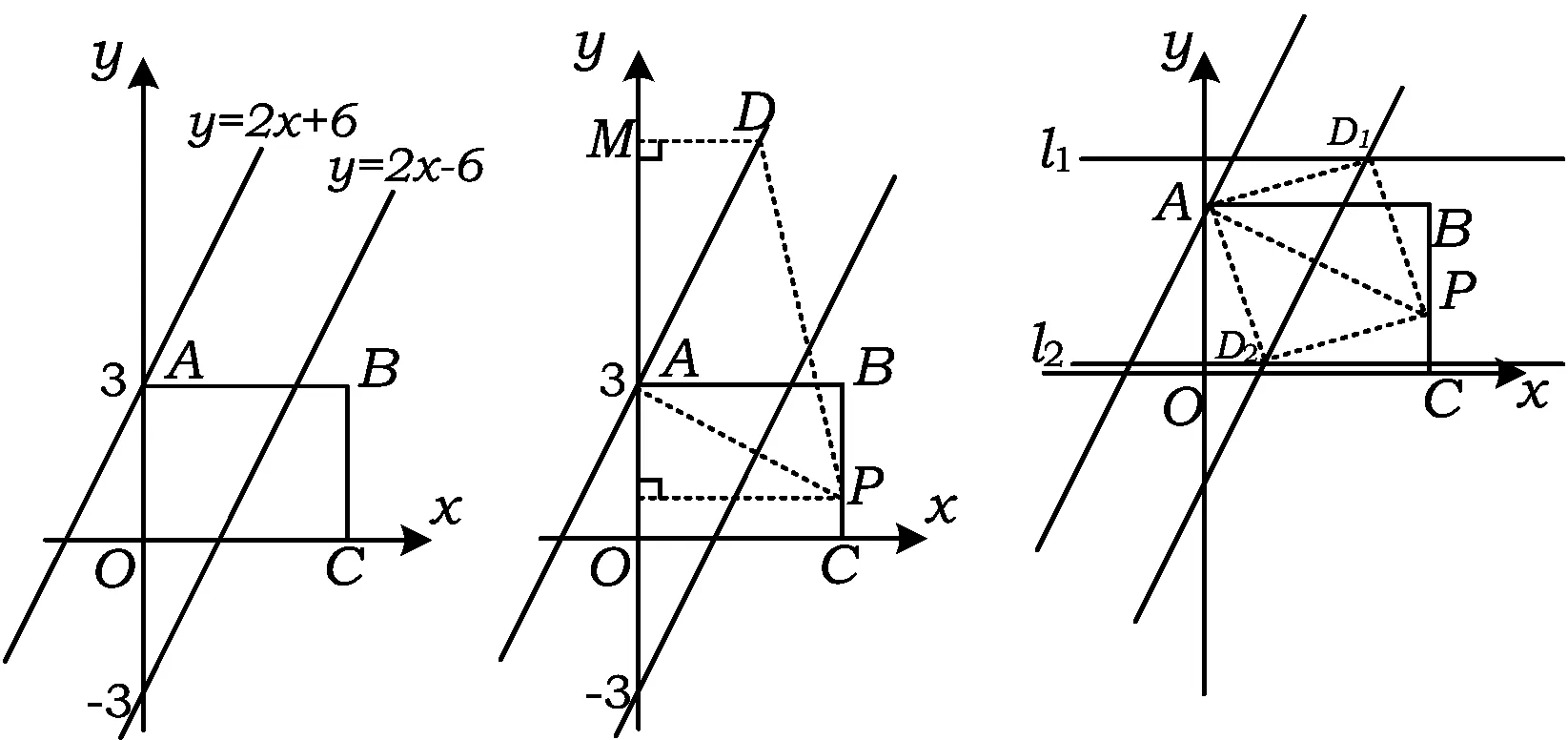
图13 图14 图15

设计意图如图14，∠DAP的直角顶点A在直线AD上，点A同时也在y轴上，为了方便求点D坐标，把“一线”选择为y轴，即过点D,P做y轴的垂线段，构成K字型全等基本图形.如图15，当点D在直线y=2x-6上时，选择过点D1的水平线l1来做为基本图形中的“一线”，构造K字型基本图形.通过此题多种情况的讨论，运用多种不同方法的构造K字型全等三角形，进一步增强学生构造K字型全等图形在综合题中的应用.

3 K字型相似

3.1 一线3个直角

如图16，将含30°角的直角三角板的直角顶点C落在直尺的边上，旋转三角板，并保证直角顶点C在直尺边上，在转动的过程中，直角顶点C的左、右2侧互余的那对锐角还存在吗？

如果从斜边的2个端点A,B向直尺的边所在的直线作垂线段，是否还存在一对相等的斜边？所构成的Rt△AEC与Rt△BFC还全等吗？如果不全等，它们又是什么关系？

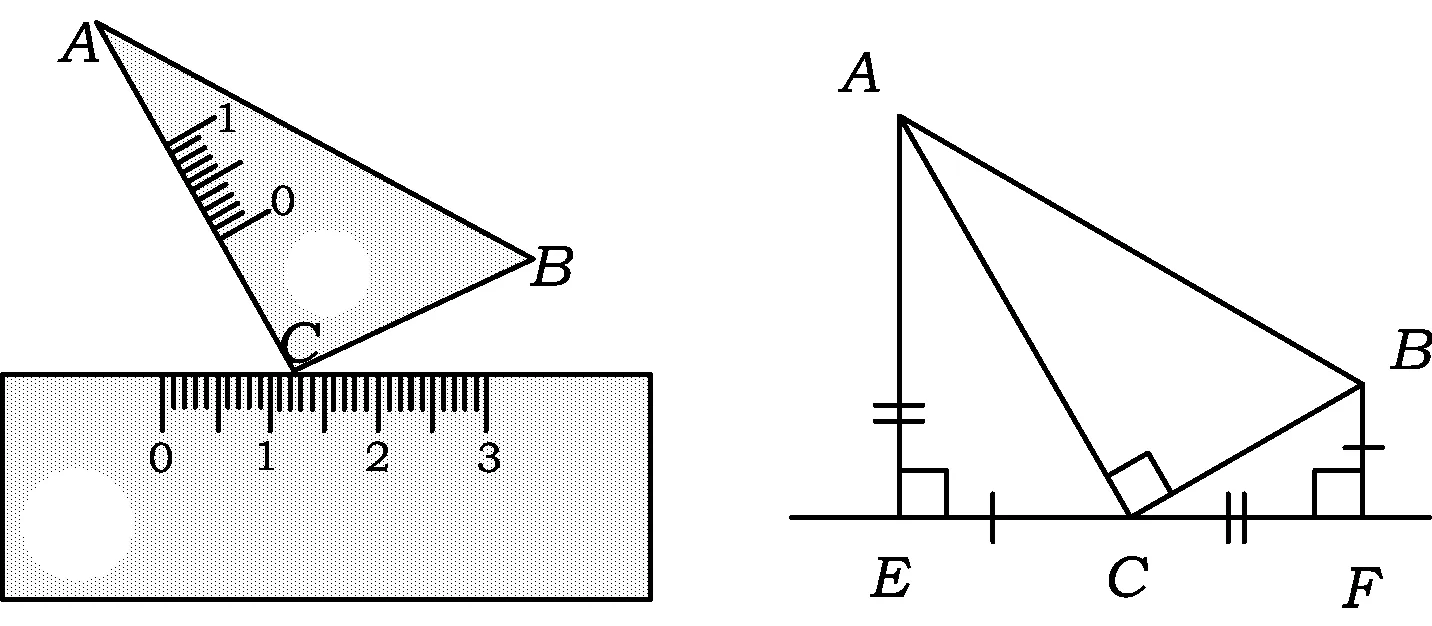
图16 图17

如图17，通过旋转另一块直角三角形，即只提供3个直角，削弱了斜边对应相等的条件，从而由K字型全等自然的过渡到K字型相似的基本图形.

条件∠AEC=∠ACB=∠BCF= 90°，且3个直角都在同一直线上.

小型紧凑化是高功率脉冲驱动源的一个重要发展方向[1-4]，能够产生近似方波脉冲的Marx发生器受到了广泛关注[5-8]。一般将传统Marx发生器中的电容器改为脉冲形成网络，可使发生器输出近似方波脉冲，再将各级脉冲形成网络以Marx发生器的形式进行叠加，即可达到增加输出功率、大幅减小脉冲驱动源体积的目的。

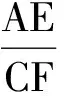
练习4如图18，在平面直角坐标系中，四边形ABCO为矩形，点B的坐标为(8，4)，把△OBC沿着对角线OB翻折，求点C的对应点C′的坐标.

图18 图19

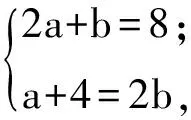
解得

3.2 一线3个等角

如图20，如果把直角三角板45°角的顶点C放在直尺的边上，转动三角板，并保证45°角的顶点C始终在直尺边上，请问∠ACB左、右2侧的2个角之和是多少？在三角板转动的过程中，这个值是否会发生变化？

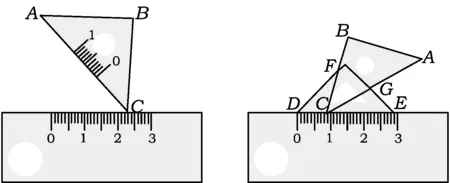
图20 图21

如图21，2块等腰直角三角板叠放，使得点D,C,E都在直尺边上，∠FDC,∠ACB∠GEC这3个角在大小上有什么关系？△FDC与△GEC有什么关系？

分析有了前面的铺垫，学生不难发现由∠GCE=∠DFC，∠FDC=∠GEC，得△FDC∽△GEC.

请学生整理图21中的条件、结论(写成已知、求证的形式)及相应的证明过程.

条件∠FDC=∠FCG=∠GEC=45°，且这3个角的顶点在同一直线上.

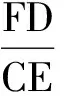
思考如果把这同一直线上的3个角换成60°或30°，那么还能得到如上的K字型相似三角形吗？如果换成其他锐角呢？

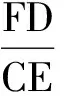
若教师只是停留在实践的层面，而未能引导学生在头脑中建构起相应的数学对象的心理表征，则很难发展真正的数学思维.因此，在动手操作过程中，相对于具体的实物操作活动，教师更应强调“操作活动的内化”，用操作活化、深化学生的数学思考，引领学生发现一般性的数学规律，才能真正发挥实践的价值.

练习5如图22，在等边△ABC中，D为BC上一点，E为AC边上一点，且∠ADE=60°，BD=3，CE=2，则△ABC的边长为______.

(2010年辽宁省沈阳市数学中考试题)

此题在等边三角形的背景下满足“一线：BC，3个等角：∠ABD=∠ADE=∠EDC=60°”，得到△BAD∽△CDE.学生运用相似性质进行推理和计算不难得出结果.

图22 图23

练习6如图23，在△ABC中，∠BAC=90°，AB=AC=1，D是BC上一个动点(不与点B,C重合)，在AC上取点E，使∠ADE=45°.

(1)求证：△ABD∽△DCE；

(2)设BD=x，CE=y，求y关于x的函数关系式；

(3)当x为何值时，△ADE是等腰三角形？

(2005年湖南省岳阳市数学中考试题)

此题的3个小题各有特点，却又紧密相联：第(1)小题学生只要能识别“一线：BC,3个等角：∠ABD=∠ADE=∠ECD=45°”,得到△BAD∽△CDE的K字型相似即可；第(2)小题与第(1)小题紧密相联，运用第(1)小题中的对应边成比例即可解决；第(3)小题的关键是分类讨论，要考虑等腰的几种不同情况.

设计意图在实际操作中，学生容易将三角板的其他顶点放在直尺的边上，很自然地从直角迁移到45°，30°，60°的情形，继而推广到更一般角的情形，体现了特殊到一般的数学思想.通过类比探究，把K字型基本图形由全等推广到相似,再到普通相似.

4 辨别真伪

在课本中利用相似三角形测量树高的例子中，虽然最后也能抽取出如图24所示的英文字母K，但是通过与K字型相似基本图形的比较，发现两者的构成条件不同，结论也不同.

练习7图25是小明设计用手电筒来测量某古城墙高度的示意图，点P处放一水平的平面镜，光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处.已知AB⊥BD，CD⊥BD，且测得AB=1.2 m，BP=1.8 m，PD=12 m，那么该古城墙的高度是______m.

(2008年浙江省金华市数学中考试题)

图24 图25

与测量树高相似，只是一对相等的直角，一对相等的锐角，边的对应是平行对应.

思考这个相似图形与前面我们说的K字型相似有什么异同点呢？

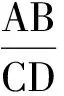
共同点：△ABP∽△CDP都处在直线BD的同侧.

设计意图此题意在让学生进一步明确，K字型相似图形中边的对应性，与测量树高、利用光的反射得到相似三角形边的对应性不同.而这个测量树高也来源于课本，与本节课的起点也来源于课本遥相呼应，再次引导学生挖掘课本例题和习题，玩好手中的学具，多思考、多探索问题的本质.

总之，教师在复习课中揭示一般性的规律时，不妨从学生的身边实际出发，从学生熟悉的学具出发，从学生感兴趣的游戏出发，让实践给枯燥的复习课注入鲜活的元素，把实践与学生的思维活动、语言表达有机地结合起来，同时注重实践的“内化”，重视“动态”实践后“静态”的数学思考.尤其在数学教学中要把握学生动手实践的契机，并由此延伸开来，既把握内涵，又涵盖外延，这样才能保证实践的效果，才能提高复习课教学的有效性.