一组函数单调性问题的错解剖析与思考
●
(台州中学 浙江临海 317000)
一组函数单调性问题的错解剖析与思考
●潘加正
(台州中学 浙江临海 317000)
函数单调性含参问题是近几年高考的热点和重点之一,也是学生感到困惑和棘手的问题之一,这些问题一般都要转化为研究导函数的图像和性质得以解决.导数是个有力的工具,作为教师,在使用这些知识(工具)的过程中,必须注意其科学性和严谨性,在求参数范围时,要注意转化的等价性.受文献[1]启发,本文对函数单调性问题的转化和化归进行了研究,以此抛砖引玉,与同行一起探讨函数单调性问题的解决策略和方法.
1 原题解答
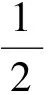
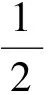

a≥[g(x)]max或a≤[g(x)]min.

笔者认为第(1)小题的分析是正确的,而第(2)小题和第(3)小题的分析有误,其转化是不等价的.剖析如下:
2 错解剖析
2.1 第(2)小题剖析
因为x∈(0,+∞),所以

即M=(0,1].因为p∈M,可取p=1,此时
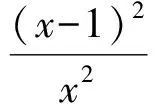
从而f(x)在定义域内为单调递增函数,与已知f(x)在定义域内不单调矛盾.

下面笔者给出第(2)小题的3种解法.

图1

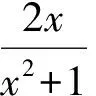
综上所述,p∈(0,1).


综上所述,0 笔者对第(2)小题进行研究,得到: 定理1已知f(x)在定义域内可导,且非常函数,则以下4个命题等价:(1)f(x)在定义域内不单调;(2)f(x)在定义域内至少存在1个极值点;(3)f′(x)=0在定义域内至少有1个解x0(x0为非偶重根);(4)在定义域内,f′(x)的函数值有正有负. 2.2 第(3)小题剖析 a≥[g(x)]min. 故f(x)在(0,+∞)上为单调递增函数,与已知f(x)存在递减区间矛盾. 下面笔者给出第(3)小题的3种解法. 解法2设f(x)为可导非常函数,则以下2个命题等价:(1)f(x)在x∈I内有单调递减区间;(2)存在区间D⊆I,使得当x∈D时,f′(x)<0成立. 利用数形结合,得 研究g(x)=-ax2-2x+1在x∈(0,+∞)的正负情况: 当a>0时,g(x)在x∈(0,+∞)上单调递减,且g(0)=1>0,故存在x0∈(0,+∞),使得f(x0)=0,因此当x∈(x0,+∞)时,g(x)<0,即f′(x)<0,亦即f(x)在(x0,+∞)上单调递减. 综上所述,a>-1. 笔者对第(3)小题进行研究,得到: 定理2已知f(x)在定义域I内可导,且非常函数,则以下3个命题等价:(1)f(x)在x∈I内有单调递减区间;(2)f′(x)<0在x∈I内有解;(3)存在区间D⊆I,使得当x∈D时,f′(x)<0成立. 罗增儒教授曾在文献[2]中提出错题分析必须坚持的基本态度:(1)解题错误的产生总有其内在的合理性,解题分析首先要对合理成分做充分的理解;(2)要通过反例或启发等途径暴露矛盾,引发当事者自我反省;(3)要正面指出错误的地方,具体分析错误的性质;(4)作为对错解的对比、补救或纠正,给出正确解法是绝对必要的.笔者正是在罗增儒教授的理论指导下进行解题分析实践和错题分析的.当然由于每个人看待同一个错解会有不同的看法,笔者的看法可能还存在问题或有不完整性,欢迎同行的批评和指正! [1] 吕增锋.“心动、生情、钟爱”—分离参数法教学“情感三部曲”[J].中学数学教学参考,2012(6):19-21. [2] 罗增儒.解题分析—谈错例剖析[J].中学数学教学参考,1999(12):1-4. [3] 孙海琴.一道高考题的解题失误引发的思考[J].中学教研(数学),2008(11):31-32. [4] 董军胜.“看错题”现象的类型与对策[J].数学通讯,2011(3):8-11. [5] 张先军.含参数的恒成立问题[J].中学教研(数学),2012(2):36-39.

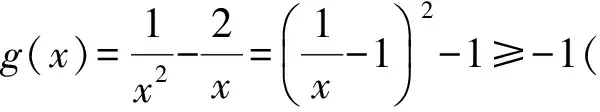





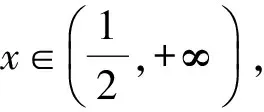

3 结束语

