圆锥曲线中相交弦的有关性质
●
(杭州市外国语学校 浙江杭州 310023)
圆锥曲线中相交弦的有关性质
●颜美玲
(杭州市外国语学校 浙江杭州 310023)
文献[1]介绍了关于圆锥曲线的一个优美性质如下:
定理1如图1,过椭圆的非对称轴的弦PQ的中点O′作2条与PQ不重合的弦AB,CD,过点A,B分别作椭圆的切线交于点M,过点C,D分别作椭圆的切线交于点N,则MN∥PQ.
笔者借助几何画板研究,发现在圆锥曲线中相交弦的有关性质,下面一一介绍.
思考1定理1中“O′为弦PQ的中点”的条件可否一般化?
经过笔者研究,知该条件无法一般化,但可以得到进一步的结论:
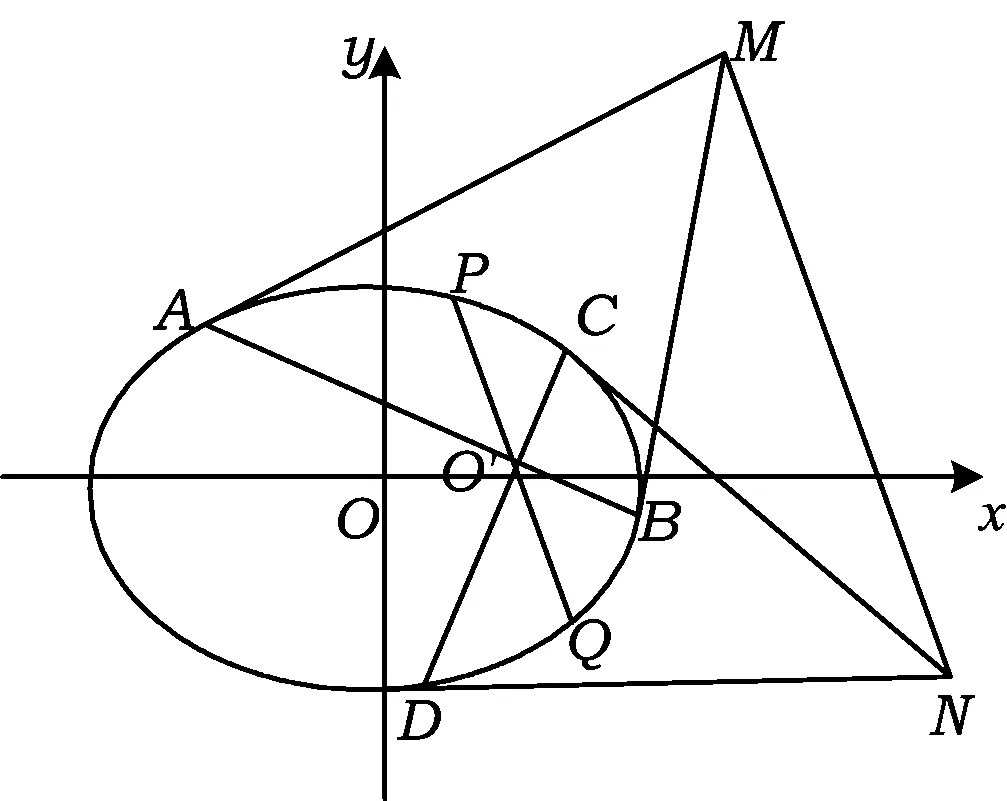
图1
性质1如图1,PQ是椭圆的非对称轴的弦,O′为弦PQ上一点,过点O′作2条与PQ不重合的弦AB,CD,过点A,B分别作椭圆的切线交于点M,过点C,D分别作椭圆的切线交于点N,则MN∥PQ成立的充要条件是O′为弦PQ的中点.
证明“充分性”的证明可见文献[1].下面证明“必要性”.


图2
从而
λ=1或x7y8-x8y7=0.
此时,若λ=1,显然O′为弦PQ的中点.若x7y8-x8y7=0,如图2可得Rt△OPE∽Rt△OFQ,则∠POE=∠FOQ,因此点P,O,Q共线,此时点O′即为点O.
思考2过椭圆2条相交弦端点的4条切线是否具有其他优美的性质?
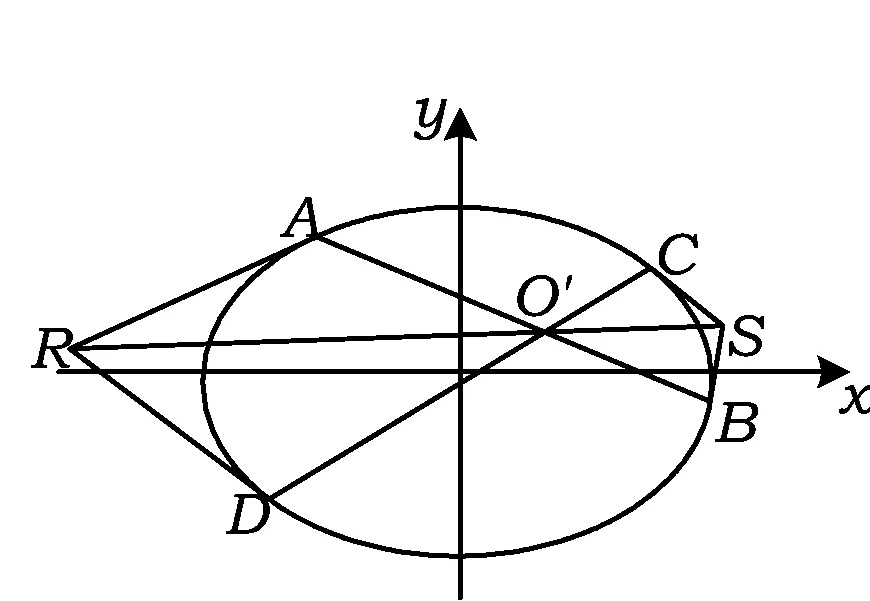
图3
性质2如图3,若弦AB,CD相交于椭圆内一点O′,过点A,D分别作椭圆的切线交于点R,过点B,C分别作椭圆的切线交于点S,则点R,O′,S共线.
分析虽然条件仍是过2条相交弦端点的4条切线,但文献[1]的方法已不适用.若设点A,B,C,D的坐标,要求出点O′的坐标计算太复杂,于是笔者考虑能否用其他方法证明,发现可利用如下引理获得.
引理设直线l1,l2的方程分别为
A1x+B1y+C1=0,A2x+B2y+C2=0,
l1,l2相交于点P,直线l3的方程为
A3x+B3y+C3=0(AiBi≠0,i=1,2,3).
若存在实数λ1,λ2,使得
λ1(A1x+B1y+C1)+λ2(A2x+B2y+C2)=A3x+B3y+C3,
则l3也过点P.
证明设直线l1,l2交于P(x0,y0),则
A1x0+B1y0+C1=0,A2x0+B2y0+C2=0,
于是A3x0+B3y0+C3=0,即l3过点P.
下面证明性质2.
证明设A(acosθ,bsinθ),B(acosφ,bsinφ),C(acosγ,bsinγ),D(acosα,bsinα),则直线CS,BS的方程分别为

联立方程组解得

同理可得

则直线AB,CD,RS的方程分别为
根据三角公式,可将方程(1),(2),(3)分别化为


接着寻找是否存在实数λ1,λ2,使得
(4)


同理可证

注在性质2中,若弦AB,CD相交于椭圆外(或上)一点O′,则点R,O′,S也共线.
思考3双曲线或抛物线也有类似的性质吗?
性质3如图4,双曲线的弦AB,CD相交于点O′,过点A,D分别作双曲线的切线交于点R,过点B,C分别作双曲线的切线交于点S,则点R,O′,S共线.
证明类似于椭圆中的情形(略).

图4 图5
性质4如图5,抛物线的弦AB,CD相交于点O′,过点A,D分别作抛物线的切线交于点R,过点B,C分别作抛物线的切线交于点S,则点R,O′,S共线.


联立方程组解得
xS=2pt2t3,yS=p(t2+t3),
同理可得
xR=2pt1t4,yR=p(t1+t4),
则直线AB,CD,RS的方程分别为

分别整理式(6),(7),(8),得


令λ=t3-t4,l=t2-t1,可得
成立,因此点R,O′,S共线.
综合性质2~4可得圆锥曲线的一个统一的性质:
定理2圆锥曲线的弦AB,CD相交于点O′,过点A,D分别作圆锥曲线的切线交于点R,过点B,C分别作圆锥曲线的切线交于点S,则点R,O′,S共线.
[1] 张俊.圆锥曲线的一个优美性质[J].数学通讯,2012(6):23-24.

