一道三角考题的编制与思考

●

(嵊州市教研室 浙江嵊州 312400)

一道三角考题的编制与思考

●施哲明

(嵊州市教研室 浙江嵊州 312400)

浙江省的数学高考连续多年在解答题的第一题考查解三角知识，主要考查正弦定理、余弦定理及面积公式、三角公式恒等变形的技能与运算能力．这类问题在已知条件、所求结论中往往会涉及三角形的边角关系、三角形的面积以及有关最值问题．解决这类问题首先要充分利用三角形的几何特征，画出图形进行分析；其次，在边、角混存的等式中，利用正弦定理或余弦定理，以达到边或角的统一.这已经成为师生的一种共识．然而，在2012年3月份参加一次高三数学模拟考试的命题中，笔者经历了一个三角试题的产生过程及由此带来的一些思考，与广大同行分享．

1 题目展示

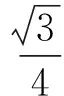
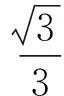
(2012年浙江省嵊州市高三数学模拟考试试题)

2 常规解答

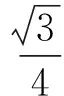
所以

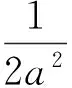
由余弦定理,得

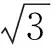
又已知c=1，故

再由sin2C+cos2C=1,得

从而

a=1．

说明在用面积公式的时候，用任何一个内角都可以作为夹角．

解法2由面积公式,得

又由余弦定理，得

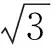
消去a2，得

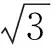
即

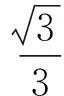
c2=a2+b2-2abcosC，

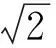
b2=a2+c2，

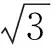
因此

3 命制过程

如图1，设想在△ABC中，边c的长度给定，若面积又给定，则△ABC的高就为定值，从而点C就在与AB平行的直线l上运动．若再添加a与b的某种关系，那么这个三角形可解，这样就有了最初的题型(例2)．

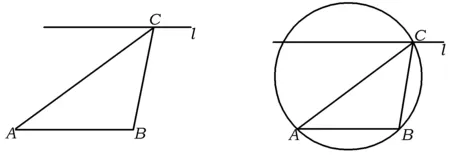
图1 图2

第(2)小题的设想过程：在c=1的前提下，若角C也是定值呢？如图2，由正弦定理可知，△ABC的外接圆就确定了，这样就可以求出这个外接圆的半径,即

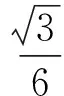
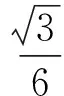
设外接圆半径为r，则由正弦定理,得

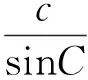
进一步思考：若边c的长度不定，而角C是定值呢？

当角C确定时，CA,CB就成射线状.若再限制a,b之间的关系，则角A,B之间是否存在某种关系？这样就有了例3：

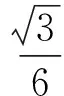
4 2点思考

思考1本题的设置过程是通过几何图形得到的，那么能不能通过几何的方法来完成这个题目的解答呢？经过思考之后，笔者又给出下面的解法．

解(1)如图3，过点C作AB的垂线，垂足为D，则由面积可知，

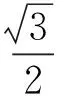
设BD=t,则

b2=(1+t)2+h2,a2=t2+h2,

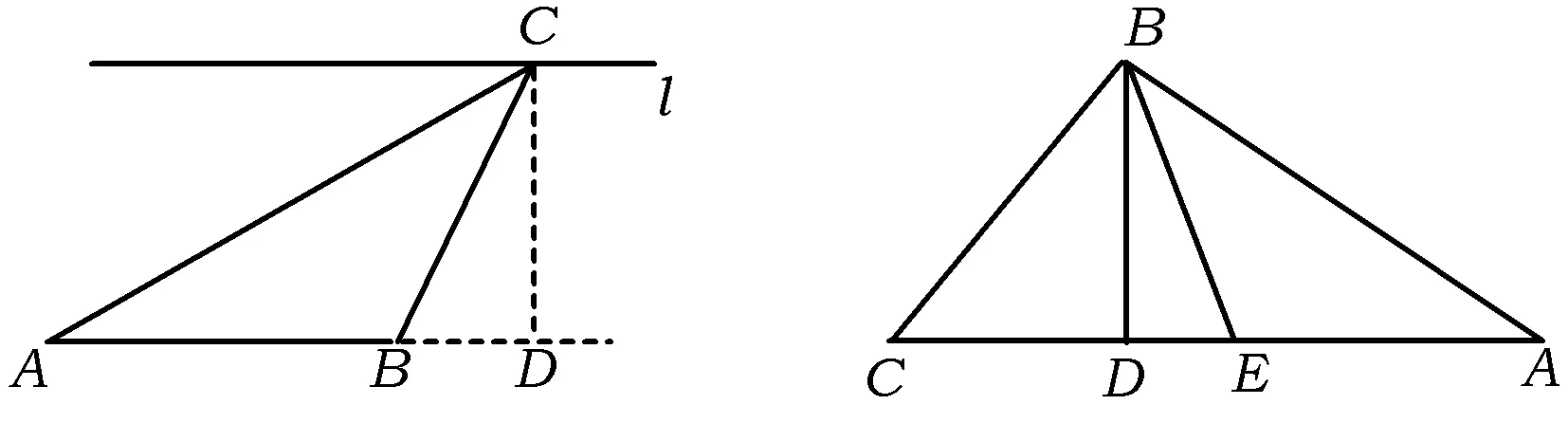
图3 图4

(2)如图4，在AC上取一点E，使得EA=EB，则

cos(B-A)=cos∠CBE.

过点B作AC的垂线，垂足为D，则

设DE=t，则

即

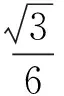
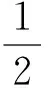
整个解答过程中没有用到任何三角公式，只是利用最原始的三角函数定义，结合几何图形来完成．或许教师在之前就有这种想法了，但是学生很难想到.

思考2学生平时习惯模仿，教师习惯运用题海战术．可遇到这样的问题，几乎没有学生会从几何的角度来思考，这是为什么呢？这对教师来说，是成功还是失败呢？至此，读者可能会问，是不是仅对这个题目而言可以用这种方法呢？我们再看2012年浙江省数学高考理科卷中的三角试题：

(1)求tanC的值；

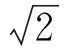
先给出参考答案，显然这是一种常规解法．

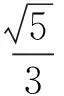
即

从而

说明解法1利用平时教师所教、学生所学，通过运用正弦定理、余弦定理和面积公式所得．但是，若从几何的角度来看这个问题，是否可行呢？

图5 图6

其次,△ABC的3个角都已经固定，但是边长不定，因此可以作一系列与直线BC平行的直线(如图6所示).若把BC固定，则三角形的3条边都确定，从而面积也为定值，这样也就有了第(2)小题．

基于上述分析，得到下面的几何解法．

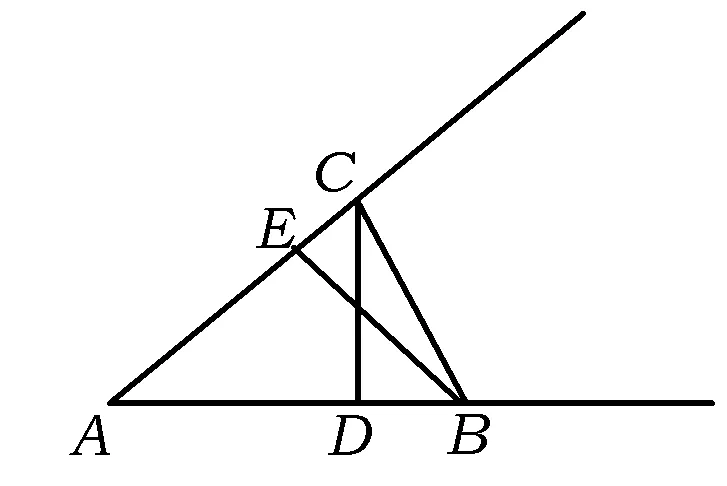
图7

解法2(1)在图7中，过点C作AB的垂线，垂足为D；过点B作AC的垂线，垂足为E.

又设BD=t，则

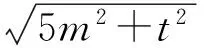
在△ABE中，可得

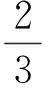
从而在△BCE中，

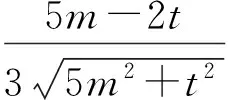
在△CDB中，

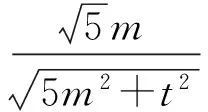
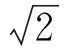
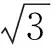
故

说明(1)运用三角函数的定义和几何图形均可解答此题，从避开解法的繁简而言，解法2恰好是此题的本源所在．

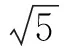
5 应用举例

例5在△ABC中，角A,B,C对应的边分别为a,b,c，且2acosC=2b-c．求角A的值.

(2013年浙江省嵊州市高三数学模拟考试试题)

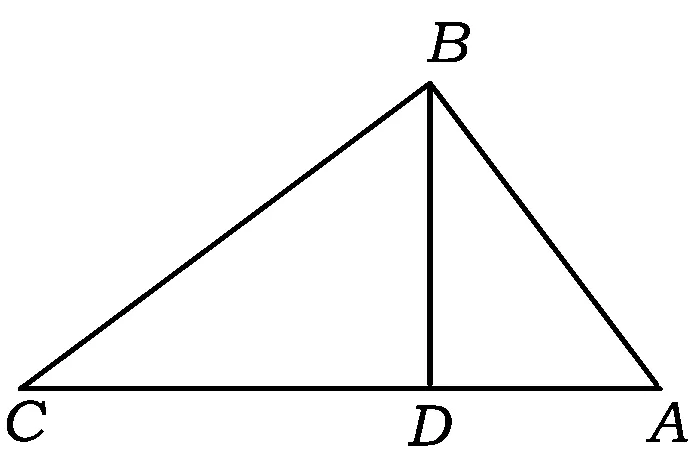
图8

解如图8，作BD⊥CA.设CD=t，则

t=acosC，AD=b-acosC，

而

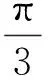
例6在△ABC中，角A,B,C所对的边分别为a,b,c，已知B=60°．

(2)若b=1，求△ABC面积的最大值．

(2013年浙江省绍兴市高三数学模拟考试试题)

解(1)如图9,作AD⊥BC于点D.由已知B=60°，得

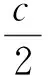
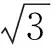
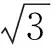
tanA= tan(30°+∠CAD)=

故

A=45°．

图9 图10

(2)若b=1，B=60°(如图10所示)，可知点B在以AC为弦的圆周上运动.当点B在AC的中垂线上时，即△ABC为正三角形时面积为最大，且最大值为