看似平常 实乃新奇 构思精巧 意境高远——一道高考试题的由来、创意及其解法理念探寻

●

(青田县教师进修学校 浙江青田 323900)

看似平常实乃新奇构思精巧意境高远
——一道高考试题的由来、创意及其解法理念探寻

●蒋海瓯

(青田县教师进修学校 浙江青田 323900)

2012年浙江省数学高考文科卷第9题，考题根植于往年高考，简洁结构，原生形态，看似平常，实乃新奇，构思精巧，意境高远，有着良好的考查检测功能与较强的命题导向功效，很值得我们一同来鉴赏与探寻．

1 试题的由来

浙江省数学高考历年来对主干知识做到“重点内容重点考，坚持不懈不动摇”．对于运用均值不等式求最值的这一高中数学重点内容坚持“连年考查，常考常新”，尤其是2010年、2011年和2012年编拟考题时，精心谋划，意蕴深远，设置“姊妹题”乃至“连环题”，题型结构相似，题设要求相近，如同并蒂花开，别具特色，考查要求却层层递进，步步深入，更加全面地考验与测试学生运用“均值不等式”等基础知识解决相应问题的技术能力与策略水平，令人赞叹不已，颇受好评．

例1若正实数x,y满足2x+y+6=xy，则xy的最小值是______．

(2010年浙江省数学高考文科试题)

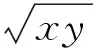
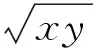
例2若实数x,y满足x2+y2+xy=1，则x+y的最大值是______．

(2011年浙江省数学高考文科试题)

本题考查要求层次提升，“所求结论”并非“题设中的一部分”，但比较容易找寻到“所求结论”与“题设条件”间的关系，只要稍作“变换”与“变形”，便能直接运用“均值不等式”解决问题.由(x+y)2=x2+y2+2xy，及已知条件得

(x+y)2-xy=1,

即

从而

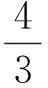
则

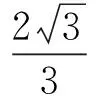
例3设x,y为实数，若4x2+y2+xy=1，则2x+y的最大值是______．

(2011年浙江省数学高考理科试题)

本题的情形与例2类似，考查的思维层次升高，不过虽然“所求结论”并非“题设中的一部分”，也不具备“关于x,y的对称性”，但也较易寻找到“所求结论”与“题设条件”间的关联，略作“变换”便能运用“均值不等式”解决问题.因为4x2+y2+xy=1，所以

(2x+y)2-3xy=1，

即

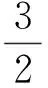
从而

得

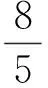
即

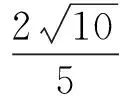
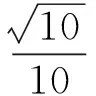
例4若正数x,y满足x+3y=5xy，则3x+4y的最小值是

( )

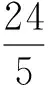
(2012年浙江省数学高考文科试题)

本题根植于例1和例2之上，但从表面难以直接寻找到“所求结论”与“已知条件”之间的本质关联与实质联系，需要先作缜密的分析、深入的剖析乃至必要的转换与化归，方能沟通“题设条件”与“所求结论”之间的关联，对学生的思维能力、分析问题和解决问题的能力提出了更高层次上的考查要求，力图发挥作为选择题中的末尾考题(共10个选择题)的压轴区分功能(详细求解见下文)，同时给我们清晰地展示了2012年这一考题的由来与命制的脉络,有着极好的命题导向功效.

2 试题的创意

创意1试题设计匠心独运，看似平常，实乃新奇，善作隐藏，巧作包装，能更加有效地检测思维的灵活性、变通性与深刻性．

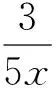
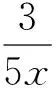
创意2试题形态简洁平和，入手容易，进口宽敞，巧置疑惑，暗藏诱惑，能更加有效地检测思想误区、思维缺失与知识缺陷．

试题结构简洁平和，呈现方式原生形态，这样的结构与形态，既为不同角度的“思维切入”预设了各种不同的运行路径，因而使问题的求解入手容易，进口宽敞，但若不作必要的“变形”与“变换”，直接求解却有一定的困难与障碍.同时考题的如此形态，如果对运用“均值不等式”求最值问题的“三大前提条件(一正二定三相等)”不及时检验与随时检测，极易发生如下所示的解题错误.由已知得

因为

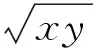
所以

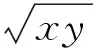
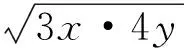
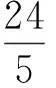
可见，本考题选项的编制可谓用心良苦，巧置疑惑，暗藏机关，极具预见性与诱惑性乃至带有迷惑性与欺骗性，能够有效地检测学生学习的思想误区、思维缺失与知识缺陷．

3 常见解法理念探寻

解法1由x+3y=5xy，得

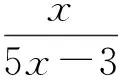
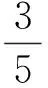
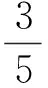
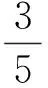
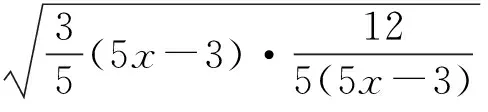
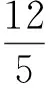
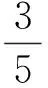
解法2由x+3y=5xy，得

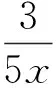
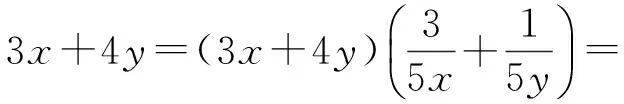
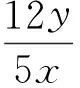
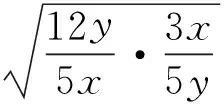
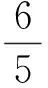
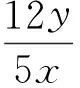
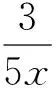
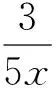
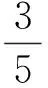
又由x+3y=5xy，得

5xy-x-3y=0，

即

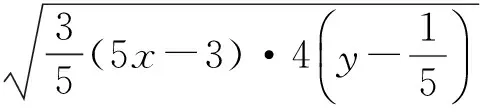
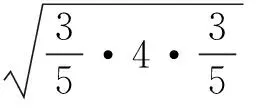
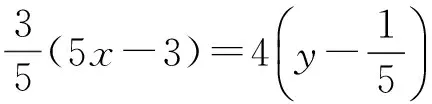
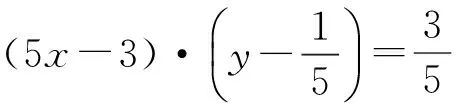
解法4由x+3y=5xy，得

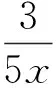
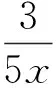
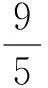
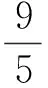
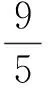
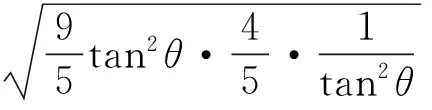
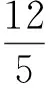
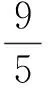
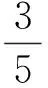
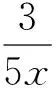
解法5令3x+4y=t(t>0)，则

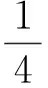
代入x+3y=5xy，消去y化简整理得

15x2-5(t+1)x+3t=0.

上式有2个正实根，从而

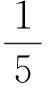
理念探寻“引元消元，方程转换”．先“引元”(引入参数t)，再“消元”(消去y)，从而将“二元函数3x+4y”的问题顺利地转化为“关于x的一元二次方程15x2-5(t+1)x+3t=0有正数根”的问题，进而“列出不等式组”加以求解．这种“函数、方程、不等式”三位一体、互相转换的变换之策略，手法新颖，思维创新，转换自然，看似平常，实乃新奇，从而绽放本题求解崭新的精彩与别样的风采．

4 一点小建议

本考题的选项可以策划与编拟得更具“干扰性”与“迷惑性”．由于“利用均值不等式求最值”时常常会忽略对“一正二定三相等”之3个前提条件的验证，估计还会有一部分学生可能会按下面的错误思路求解：

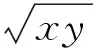
从而

3x+4y= (x+3y)+(2x+y)=

5xy+(2x+y)≥

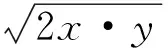
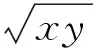
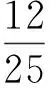
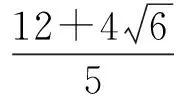
错误思路2由x+3y=5xy，得

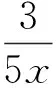
因此，如果将本试题的选项改为：

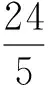
这样每一个答案都极具“干扰性”与“迷惑性”，能更加有效地诊断学生的思维缺失，暴露学生的思维误区，检测学生的思维缺陷，也就能更加有效地发挥试题的“考查功能”与“选拔功效”.

[1] 蒋海瓯.关于试卷讲评的“点滴见解”[J].中学数学教学参考，2012(5)：51-54.