每遇困难 问道于图可尔
●
(象山市第三中学 浙江象山 315700)
每遇困难问道于图可尔
●茅映丽胡庆彪
(象山市第三中学 浙江象山 315700)
解析几何是中学数学的核心内容之一,在数学高考中占有十分重要的地位,但又是学生掌握得不太好的知识领域.因此,加强解析几何问题特征、解法规律的研究与学习,提高分析与解决问题的能力,意义十分重大.本文给出一个能迅速、明确解决解析几何题及给出较细步骤的方法——问道于图法.
所谓“问道于图法”,就是在读解析几何题的过程中或在读完题目之后,先根据题意画出一个能反映本题条件与结论的图形,然后按照生成图形的各个步骤,依次将“图形语言”翻译成“数学符号语言”,一旦翻译完毕,问题也基本解决.下面举例说明之.
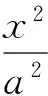
( )

(2013年浙江省宁波市高三数学第一次模拟考试文科试题)
分析本题图形的生成步骤,如表1中的第2列所示,将各步的“图形语言”按序翻译成“数学符号语言”,如第3列所示:

表1 用“问道于图法”解决例1

说明有时没有必要把图形的生成步骤(图形语言)都一一翻译成“数学符号语言”,而只需选择其关键处加以翻译.

图1
例2如图1,已知F为抛物线C1:x2=2py(p>0)的焦点,若过焦点F的直线l交C1于点A,B,使抛物线C1在点A,B处的2条切线的交点M恰好在圆C2:x2+y2=8上.
(1)当p=2时,求点M的坐标;
(2)求△MAB面积的最小值及取得最小值时的抛物线C1的方程.
(2013年浙江省宁波市高三数学第一次模拟考试文科试题)
分析第(1)小题图形的生成步骤,如表2中的第2列所示,将各步的“图形语言”按序翻译成“数学符号语言”,如第3列所示:

表2 用“问道于图法”解决例2

x1+x2=4k,x1x2=-4,

(2)从第(1)小题的p=2推广到p>0,但成图次序依旧,可类比第(1)小题的求解而得:
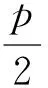

x1+x2=2pk,x1x2=-p2,

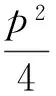
(5)
接下去只要求得弦长|AB|及点M到AB之距d, 就可得到△MAB的面积S(含p与k),再由式(5),将p用k表示, 显然可将S化成关于k的函数S=f(k), 最后求f(k) 的最小值(略).
在例1和例2的第(1)小题中,求解过程紧依其对应的作图步骤,且同步到达终点.
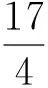
(1)求p与m的值;
(2)设抛物线C上一点P的横坐标为t(t>0),过点P的直线交C于另一点Q,交x轴于点M,过点Q作PQ的垂线交抛物线C于另一点N,若MN是C的切线,求t的最小值.
(2009年浙江省数学高考文科试题)
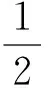
(2)图形的生成步骤,如表3中的第2列所示,将各步的“图形语言”按序翻译成“数学符号语言”,如第3列所示:

表3 用“问道于图法”解决例3

通过例3,我们再次发现:在将“图形语言”翻译成“数学符号语言”后,离解题的终极目标只是一步之遥了.需要指出的是,有时没有必要把图形的生成步骤(图形语言)都一一翻译成“数学符号语言”, 而只需选择其关键处加以翻译即可.
我国著名数学家傅种孙教授在20世纪50年代曾经指出:“每遇困难,即问道于0可尔.”这一方面是由于数学问题中几乎处处涉及关于“0”的思索,偶有疏忽,便出差错;另一方面是因为代数问题中的许多结论由自然数“0”的运算性质所决定——问道于0可尔.因此,注重发挥数“0”的解题功能显得十分重要,笔者认为:对于解析几何题而言,应注重发挥与挖掘图形的功能.行走在解析几何解题路上,每遇困难,即问道于图可尔.

