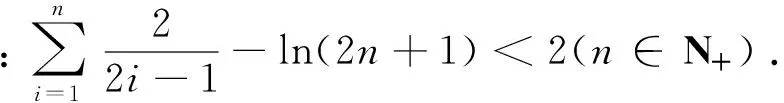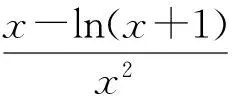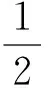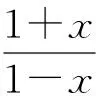一类高考压轴题的新解
●
(德清县第三中学 浙江德清 313201)
一类高考压轴题的新解
●杨新荣
(德清县第三中学 浙江德清 313201)
综观近几年来全国各省、市的数学高考压轴题,多数试题是关于含参不等式恒成立求参变量的范围.这类问题的常用解法是通过分离参变量转化为利用导数求函数的最值.这样的解题思路自然,但往往运算繁杂,有时要结合分类讨论才能解决,有时还需多次求导后才能求得最值.这使许多运算能力和应变能力较差的学生望而生畏,难以求得正解.笔者经过研究发现这类问题的一种新的解题方法.其解题本质是通过先分析命题成立的充分条件而后探求问题成立的必要条件,巧得所求参变量的取值范围.
1 温故探新,寻求解题途径

(2010年湖北省数学高考理科试题)
解法1分类讨论.

g(1)=0,
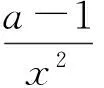
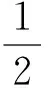
g(x) g(x)>g(1)=0, 解法2分离参变量. 上述2种解法一般学生都较难完成,下面笔者给出本题的第3种解法: 解法3利用充要条件. 而上式在x=1时,2边仍相等,故只需证 2(a-1)≥-x, 解得 上述3种解题途径,其本质都是利用导数研究函数问题,特别是解法3,充分利用了导数的几何意义求解,使解题自然而又明快.为了进一步认清解法3的本质,笔者根据导数的几何意义给出函数的2个性质. 性质1若函数f(x)与g(x)满足f(x0)=g(x0),则f(x)>g(x)在x∈(x0,+∞)上恒成立的充分条件是f′(x)>g′(x). 有了上述2个性质,我们对含参不等式恒成立求参变量范围的问题,可通过先求充分条件再求必要条件,而巧得参变量的取值范围. 例2若不等式ex-e-x≥ax在x≥0时恒成立,求实数a的取值范围. (2007年全国数学高考试题) 解(充分条件)当x=0时,不等式2边相等.由性质1知,欲证ex-e-x≥ax在x≥0时恒成立,只需证ex+e-x≥a恒成立.由此得充分条件为a≤2. 因此,a≤2是原不等式在[0,+∞)上恒成立的充要条件. 例3设函数f(x)=ex-1-x-ax2,当x≥0时,f(x)≥0恒成立,求实数a的取值范围. (2010年全国数学高考新课标卷试题) 解(充分条件)由f(x)≥0得 ex-1-x≥ax2, 例4已知f(x)=x2+2x+alnx,f(2x-1)≥2f(x)-3在[1,+∞)上恒成立,求实数a的取值范围. 分析令g(x)=f(2x-1)-2f(x)+3,由f(2x-1)≥2f(x)-3在[1,+∞)上恒成立,得 g(x)=2(x2-2x+1)-a[lnx2-ln(2x-1)]≥0 在[1,+∞)上恒成立.此时采用变量分离根本没法解决问题,若用性质1和性质2,则可得如下解法: 解(充分条件)令g(x)=f(2x-1)-2f(x)+3,由g(x)≥0得 2(x2-2x+1)≥a[lnx2-ln(2x-1)], 当x=1时,不等式2边相等.由性质1知,只需 恒成立,即2x(2x-1)≥a恒成立,从而a≤2.由此得充分条件为a≤2. 即 a≤2. 因此,a≤2是原不等式在[1,+∞)上恒成立的充要条件,即实数a的取值范围为(-∞,2]. 例5已知函数f(x)=x-ln(x+a)的最小值为0,其中a>0. (1)求a的值; (2)若对任意的x∈[0,+∞),有f(x)≤kx2成立,求实数k的最小值; (2012年天津市数学高考模拟试题) 解第(1)小题:a=1.第(3)小题(略). (2)(充分条件)由f(x)≤kx2得 x-ln(x+1)≤kx2, 用以上方法还可以解决很多类似的高考把关题,例如: (2006年全国数学高考理科试题) (2008年全国数学高考理科试题) 在中学数学解题教学中,教师若能引导学生从数学的基本概念和知识出发,分析探索数学问题的解题新途径,这不但能教给学生知识,而且在这种探索过程中培养了学生的数学能力,这才是数学教育之根本.如含参不等式恒成立求参变量范围的问题,常用的解法为变量分离法、分类讨论法等等,但本文通过利用导数的几何意义,比较2个函数的递增或递减的速度和适时应用洛必达法则求其不等式恒成立的充要条件——解题思路清晰,解法简明,既培养了学生的解题能力又传授了新的知识,真可谓事半功倍. [1] 张国治.一类导数高考压轴题的通解[J].数学教学,2012(11):42-44.
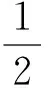




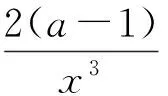

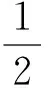

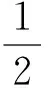
2 提炼新知,归纳解题方法

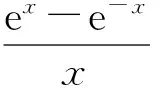


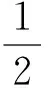
3 应用举例,提升解题能力