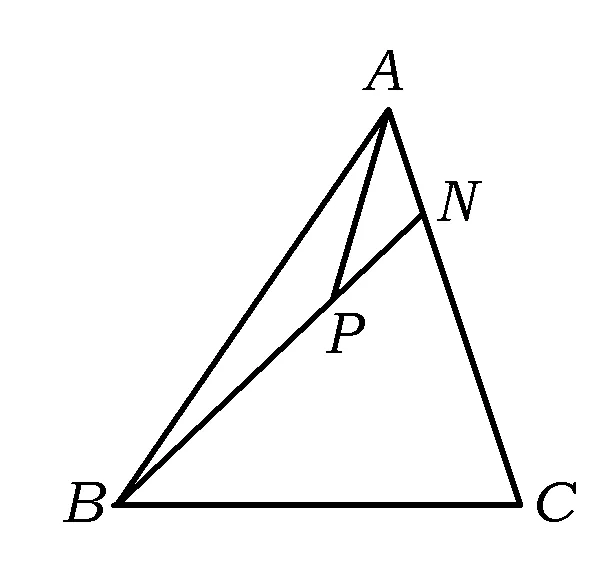
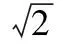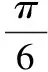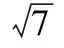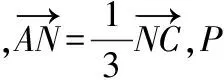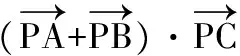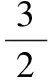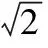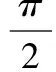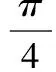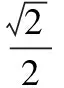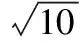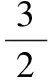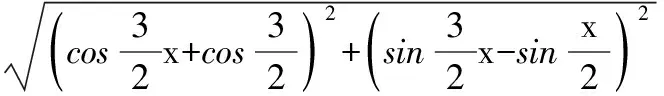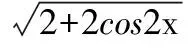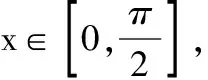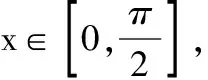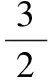平面向量及其运用
● (杭州市高级中学 浙江杭州 310003)
平面向量及其运用
●陈利民(杭州市高级中学 浙江杭州 310003)
1 考点回顾
平面向量是高中数学最重要的工具性知识之一,它兼具几何形式和代数形式双重身份,成为高中数学知识的交汇点之一.近几年的高考,平面向量的考查主要体现在2个方面:一是平面向量相关概念、线性运算及数量积运算的考查,高考中或直接考查或用以解决有关长度、垂直、夹角、判断多边形的形状等,例如浙江省数学高考2010年第16题、2011年第14题、2012年第5题都是向量夹角、模、数量积运算的问题;二是考查平面向量的综合应用.平面向量常与平面几何、解析几何、三角函数等内容交叉渗透,使数学问题的情境新颖别致,此类问题往往用向量语言表述题干,而问题的解决要涉及其他知识的综合运用,例如2010年全国数学高考理科第11题(向量与圆)、上海市数学高考理科第13题(向量与双曲线)、2011年浙江省数学高考第17题(向量与椭圆).
纵观近几年的高考试题,在兼顾向量相关概念与运算的同时,试题中往往渗透明显的几何背景,解题中若能注意到题干涉及的几何背景,综合运用解三角形(正、余弦定理)、解析几何及函数的知识与方法,将会起到事半功倍的效果.
2 典例剖析
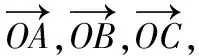
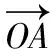

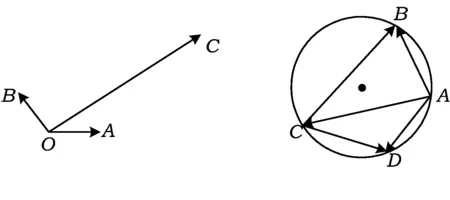
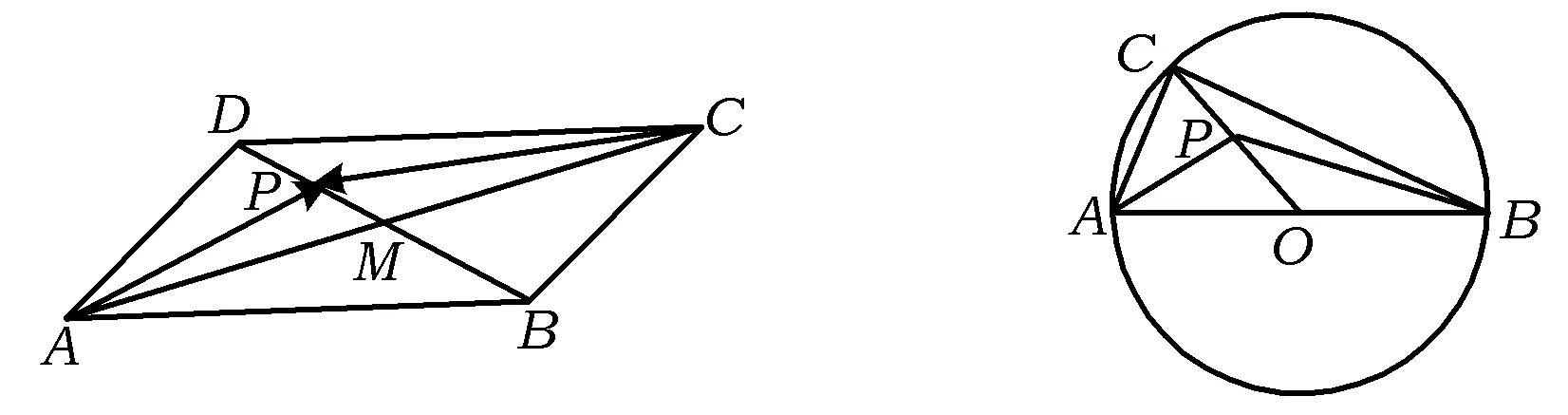
图1 图2

( )
(2011年全国数学高考理科试题)
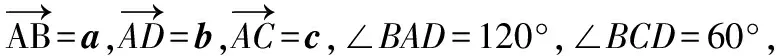
评注本题考查平面向量夹角与模的概念、数量积运算等基础知识,解题的关键是构造题设条件下的几何模型.平面向量构造几何背景的试题常常以平面几何的基本图形,例如三角形、四边形、正六边形、圆等为切入口,突出考查学生对问题的理解转化能力和数形结合能力.此类问题的常规解法是抓住平面向量“数”与“形”这2个特征进行思考,努力透析向量条件下的几何模型,有些时候需要建立适当的坐标系,借助坐标运算来解决问题.
例3在直角坐标系中,△ABC的2个顶点A,B坐标分别为(-1,0),(1,0),平面内2个点G,M同时满足下列条件:
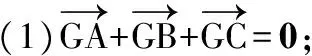
(2)MA=MB=MC;
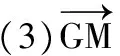
则△ABC的另一个顶点C的轨迹方程为______.
分析本题实际上是向量背景下的解析几何问题,解题的关键是要理解和转化向量表述下的题设条件的几何含义,正确运用求动点轨迹的方法来解决问题.
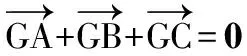
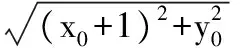
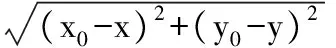
得
x0=0,
即
(1)
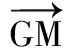
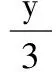
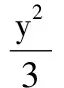
又因为点C不能在x轴上,所以点C的轨迹方程为
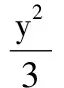
评注本题重点考查动点轨迹的求法,兼顾向量的线性运算,对学生运算能力有一定要求,体现了向量知识与解析几何知识的有机结合.条件表述采用向量形式,背景新颖别致,要求学生理解掌握三角形重心、外心与平面向量的关系.此类问题的解决,除了必须具备向量概念、线性运算、数量积运算等基础知识外,更侧重于考查解析几何问题求解的技能与方法,突出考查学生综合运用数学知识解决问题的能力.
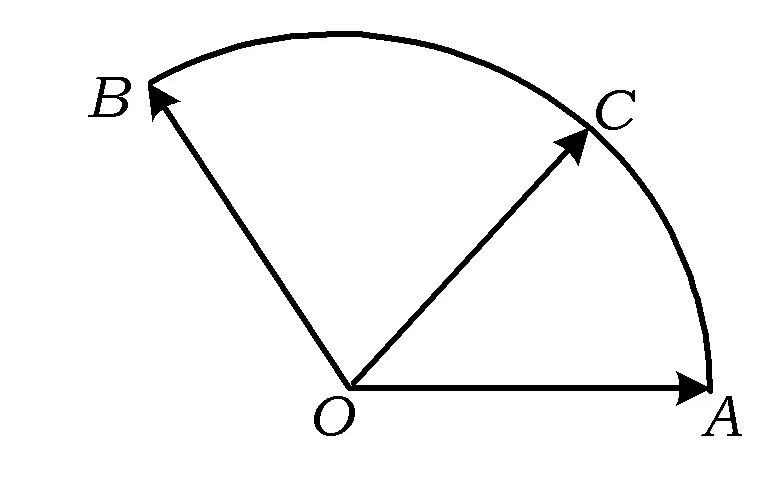
图3
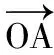
(2009年安徽省数学高考理科试题)
分析要求x+y的最大值,必先建立它的目标关系式.
解法1若从向量数量积运算考虑,可得
则
即
(x+y)2≤4,
从而
x+y≤2.
解法2引进角参数,设∠AOC=α,则
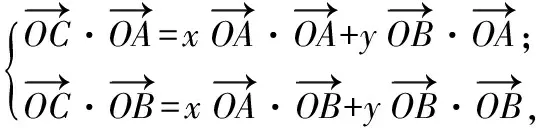
即
从而x+y= 2[cosα+cos(120°-α)]=
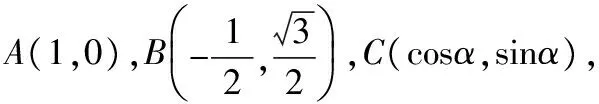
于是
评注本题解法较多,解法1从向量数量积运算出发,结合不等式性质解决问题;解法2引进角参数,运用向量数量积的运算性质,从而建立起x+y关于参数α的目标函数式;解法3建立直角坐标系,运用向量的坐标运算,得到x+y关于参数α的目标函数式,后2种方法都要涉及三角函数的化简与恒等变形,对学生综合运用知识的能力提出了较高要求.
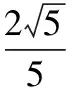
(1)求cos(α-β)的值;

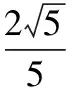
|a-b|2= 2-2(cosαcosβ+sinαsinβ)=
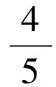
从而
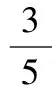
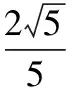
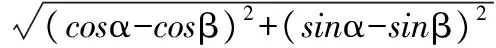
即
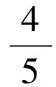
从而
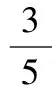
(2)注意到条件角与所求角之间的联系,运用三角变换可得结论
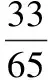
评注本题是向量背景下的三角函数问题,考查向量的坐标运算和数量积运算,重点是三角函数两角差余弦公式和角变换公式的运用,考查学生的推理和运算能力.事实上,平面向量与三角函数的综合运用一直是高考命题的一个热点问题,它的主要形式是平面向量与三角函数化简求值结合、与三角函数图像性质结合、与解三角形相结合等,其本质是三角变换与函数性质的综合运用,从而构建具有一定思维能力要求的中等难度题型.
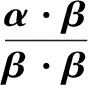
( )

(2012年广东省数学高考理科试题)
分析本题在向量原有运算基础上定义了一种新的运算,理解和转化新定义是解题的关键.
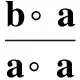

从而
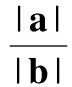
且
a∘b=2cos2θ>1,
于是
1 故 两式相乘得 得 2 所以 k1k2=3. 又由|a|≥|b|>0,得 k1=3,k2=1, 于是 ( ) 2.一质点受到平面上的3个力F1,F2,F3(单位:牛顿)的作用而处于平衡状态.已知F1,F2成60°角,且F1,F2的大小分别为2和4,则F3的大小为 ( ) 图4 ( ) ( ) ( ) 图5 图6 8.已知向量a=(sinα,cosα),b=(6sinα+cosα,7sinα-2cosα),设函数f(α)=a·b. (1)求函数f(α)的最大值; (1)求a·b及|a+b|; 参考答案 8.解(1)因为 f(α)=a·b= sinα(6sinα+cosα)+cosα(7sinα-2cosα)= 6sin2α-2cos2α+8sinαcosα= 4(1-cos2α)+4sin2α-2= 所以 (2)由第(1)小题可得 从而 即 故 因为 所以 a2=b2+c2-2bccosA= 得 cos2x, cosx>0, 从而 |a+b|=2cosx. (2) f(x)=cos2x-4λcosx, 即 f(x)=2(cosx-λ)2-1-2λ2. ①当λ<0时,当且仅当cosx=0时,f(x)取得最小值-1,这与已知矛盾;
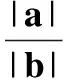
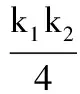
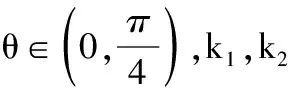
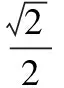

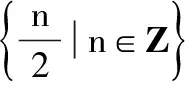
3 精题集萃