旋转式惯导系统光纤陀螺在线自标定方法

周元，邓志红，王博，付梦印

(北京理工大学 自动化学院，北京100081)

精确标定惯性器件的零偏、标度因数误差、安装误差等并加以补偿是提高惯导系统精度的关键一步.对这些参数除了在实验室标定外，还可以在现场标定.现场标定是在惯性导航系统处于载体安装状态下进行的，相对于实验室标定来说，现场标定环境更接近于系统的实际工作环境，针对性强，对于提高惯导系统的实际使用精度意义重大.但是在线标定无法利用转台等试验设备，只能依靠重力场、地球自转角速度、载体的运动及载体上其他辅助导航设备(如卫星接收机、里程计等)来完成.传统的光纤陀螺在线标定方案是将其零偏列入初始对准状态向量，采用Kalman滤波估计［1］，该方法通常选择导航系统速度误差作为外观测量，在静基座条件下可用系统实时解算的速度代替［2］.但以地速误差为外观测量的初始对准Kalman滤波的可观测性低［1］，滤波估计的效果不理想.

近年来，误差旋转调制技术逐渐成为捷联惯导领域的研究热点.旋转式惯导系统具有与平台式系统类似的框架和转轴，但功能不同，仅相当于在捷联惯导系统外部加上转动机构和测角装置，通过使惯性测量单元(inertial measurement unit，IMU)旋转来抑制惯性器件误差的积累，成本较平台式系统大幅降低［3-4］.旋转式IMU可控制的角运动特性为光纤陀螺在线自主标定提供了新思路.利用IMU旋转(包括连续旋转和多位置转停)可改善初始对准可观测性从而提高对惯性器件误差参数的估计精度［5-7］，但旋转机构的误差也将引入新的误差源［8］.为实现光纤陀螺误差的在线标定，本文根据旋转式IMU的光纤陀螺输出模型特点，提出了一种易于实现的基于递推最小二乘(recursive least square，RLS)估计的光纤陀螺误差参数高精度在线快速标定方案，并给出基于硬件系统的实现方法.仿真结果表明了所提出的方案的有效性，为该算法的工程化实现奠定了基础.

1 旋转式IMU光纤陀螺解耦RLS估计标定方案

1.1 光纤陀螺的在线标定数学模型

导航系统平台(包括物理平台和数学平台)漂移主要是由陀螺的安装误差、标度因数误差和漂移误差等引起的［9］，其中安装误差、高次项误差和噪声等复杂因素一般难以估算，在线标定中可以忽略.慢变漂移分量会随着工作过程中各种条件的改变发生缓慢变化.陀螺的逐次启动漂移取决于陀螺启动时的各种随机因素，一旦启动完成，改漂移便成为一个固定的常数［10］，标度因数误差也可以用一个随机常数来描述.因此在初始对准阶段较短时间内需要进行标定的误差项即为陀螺的逐次启动漂移和陀螺的标度因数误差，由此得到光纤陀螺在线标定数学模型:

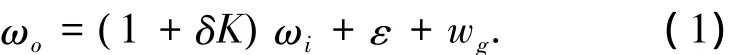
式中:ωi和ωo分别为光纤陀螺的输入角速度和输出角速度，δK为标度因数误差，ε为零偏，wg为随机噪声.

1.2 旋转式IMU光纤陀螺解耦RLS估计数学模型

在旋转式捷联惯导系统中，从IMU坐标系到载体坐标系的方向余弦矩阵(称为旋转矩阵)数学模型由旋转机构的结构和旋转方案决定，对于内环转轴与IMU坐标系的x轴重合，外环转轴与载体坐标系z轴重合的双轴旋转式惯导系统，令内环轴、外环轴周期性连续旋转，每旋转一周改变转向，则旋转矩阵表达式如下:

式中:角标p表示IMU坐标系，其三坐标轴分别与IMU敏感轴重合;αj表示转轴 j转过的角度(j=x，z).

在静基座下，旋转式惯导系统光纤陀螺所敏感到的角速度为

式中:角标i、n、e分别表示地心惯性坐标系、地理坐标系(选为导航坐标系)、地球坐标系;L为初始对准时载体所在纬度位置，ωie为地球自转角速率，ωrx和ωrz分别为转轴x和转轴z的旋转角速度.

对于双轴旋转式惯导系统，可以仿照平台式系统对其进行粗调平，使俯仰角、横滚角近似为零，而方位角可以通过解析法近似求得，则姿态矩阵可以写成以下形式:

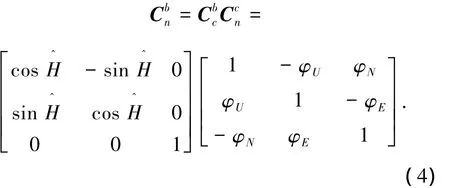
根据式(1)可以得到旋转式捷联惯导系统静基座下光纤陀螺的输出模型为

式中:“～”表示该参数为光纤陀螺的测量值，下标x、y、z表示IMU坐标系的坐标轴方向;δKj为光纤陀螺标度因数误差，ωipj为IMU相对惯性空间的角速度在IMU坐标系下的分量，εj和wgj分别表示陀螺的零偏和噪声(j=x，y，z).

将式(2)～(4)代入式(5)，其中参数 φk、εj、δKj、ωie均为小量，将由它们相乘得到的二阶、三阶小量忽略，可得旋转式捷联惯导系统静基座下光纤陀螺的输出模型的简化形式:

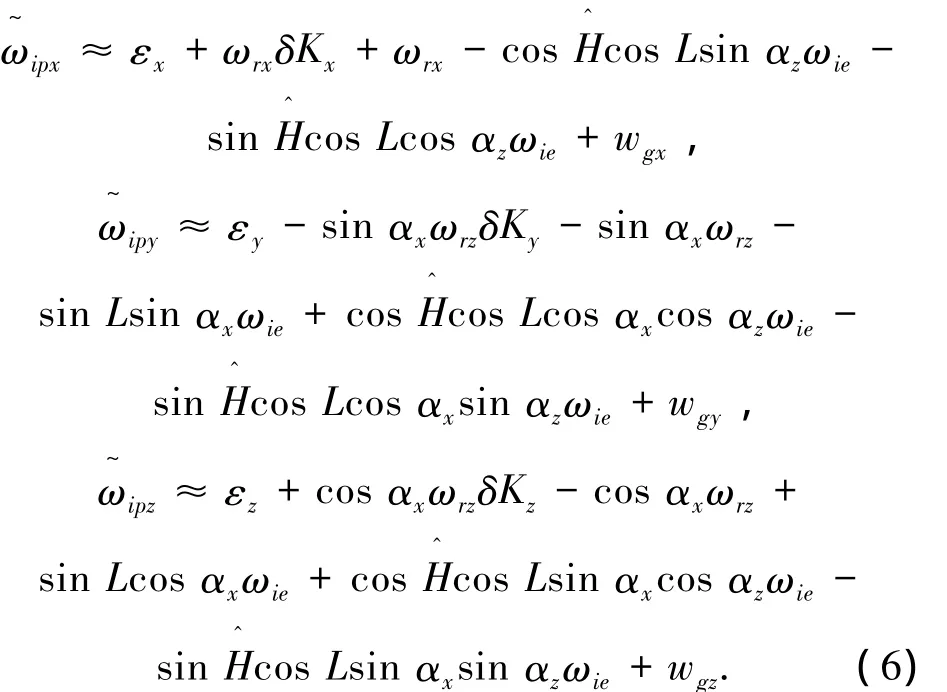
式中:L的值已知，ωrx、ωrz与 αx、αz可以分别从旋转机构的角速度传感器与角度传感器实时测得，由此可以得到各陀螺零偏与标度因数误差的线性组合的观测量.式(6)的简化近似略去了IMU陀螺组各通道之间的耦合，则每个光纤陀螺可视为一个独立的通道，取其零偏和标度因数误差作为状态量，采集光纤陀螺输出值进行最小二乘估计，可以实现光纤陀螺在线标定.各通道的观测量分别为

为充分利用陀螺测量值，使用RLS估计以提高估计精度.根据旋转IMU的光纤陀螺解耦输出模型，各通道数据最小二乘估计解算流程相同，其递推公式为

应用最小二乘标定时，取状态向量X初值为零，Pj(0)和Rj分别按照光纤陀螺的标称值取值，其中，Pj(0)为对角矩阵，它的对角元素为光纤陀螺的零偏和标度因数误差的平方，Rj为光纤陀螺噪声方差.

1.3 光纤陀螺误差解耦RLS算法估计性能分析

对于在地球表面运动的车辆、舰船等载体，光纤陀螺捷联式惯导系统初始对准的Kalman滤波状态方程可写为

式中:X为惯导系统初始对准状态向量，WV为系统噪声向量，系统状态矩阵与系统噪声系数矩阵中各子阵表达式如下:

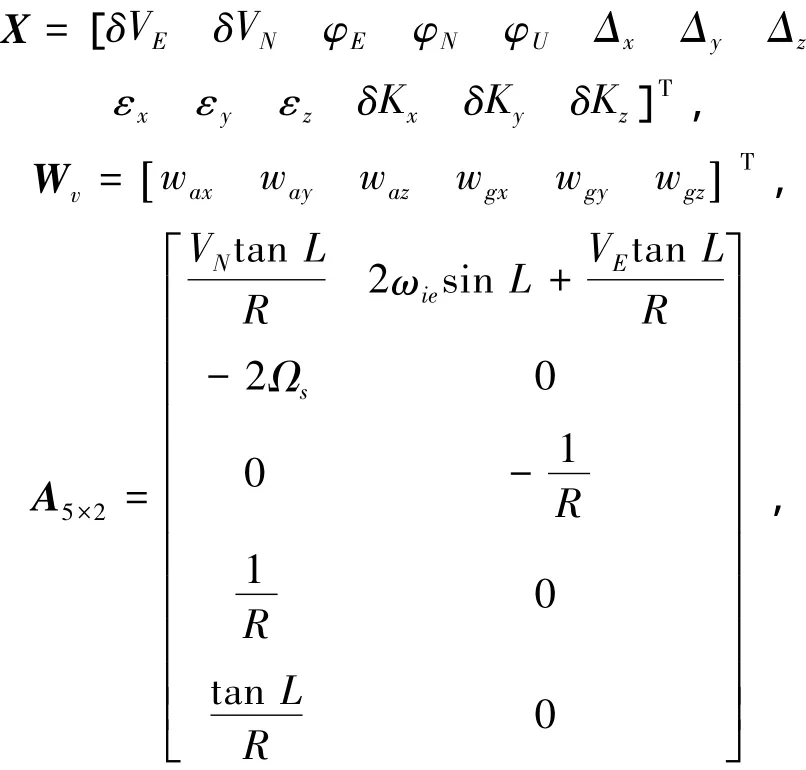
式中:下标b表示载体坐标系，其坐标轴x、y、z分别指向载体右、前、上;R为地球半径;c11，c12，…，c23为载体姿态矩阵的各元素;Vk表示载体速度，δVk表示其误差;fk为地理坐标系下的比力分量(k=E，N，U);ωibj为载体相对惯性空间的角运动，Δj和waj分别为加速度计的零偏和噪声(j=x，y，z).

初始对准中光纤陀螺标定可用解耦RLS估计替代，因此可以将状态向量中陀螺零偏和标度因数误差删除，从而降低状态方程阶数.Kalman滤波器的运算量与其阶数的三次方成正比.若系统状态方程阶数为n，观测方程阶数为m，则完成一次递推计算需要完成4n3+(1+4m)n2+(2m2+2m)n+m3次乘除运算和4n3+(4m-2)n2-(2m+1)n+m3次加法运算［10］.原Kalman滤波状态方程为14阶，观测方程为2阶，而删除光纤陀螺零偏和标度因数误差状态量以后，系统状态方程为8阶，观测方程为2阶，可知降阶系统的Kalman滤波乘除法、加法运算量分别下降至原系统的21.12%和19.84%.

对于使用参数辨识法进行初始对准的捷联惯导系统，如果已知陀螺的等效东向漂移，则可以提高求方位失准角初值的精度［11］.利用最小二乘法标定的陀螺误差参数求得陀螺东向等效漂移，可以改善参数辨识法对准精度.

2 光纤陀螺误差参数的解耦RLS估计仿真研究

通过Matlab软件仿真实验，比较解耦RLS估计和捷联惯导初始对准Kalman滤波在光纤陀螺在线标定方面的性能.仿真条件设定如下:静基座初始对准过程中，载体所在纬度为30°，载体的航向角为30.06°，为 30°，粗调平后俯仰角、横滚角均为0.06°，光纤陀螺的零偏为0.01°/h，标度因数误差为10×10-6，陀螺随机噪声为标准差为0.005(°)/h的高斯白噪声.加速度计的零偏为10-4g，噪声标准差为0.5×10-4g.惯性器件的采样频率为100 Hz，其中旋转式惯导系统的转轴结构与式(2)系统相同，其双轴均以5(°)/s的角速度旋转.分别进行900 s的最小二乘估计和Kalman滤波，光纤陀螺零偏和标度因数误差的估计误差如图1、2所示.

图1 2种方法陀螺零偏的估计误差比较Fig.1 The comparison of estimation errors of the two methods about gyro biases

图2 2种方法陀螺标度因数误差的估计误差比较Fig.2 The comparison of estimation errors of the two methods about scale factor errors

在仿真实验后期(t=450～900 s)，2种方法的估计误差绝对值的均值如表1.

根据仿真结果可知:相对捷联惯导初始对准Kalman滤波，旋转IMU光纤陀螺解耦RLS估计的2种陀螺误差参数的平均标定误差分别下降至52.41%和46.68%，证明采用解耦近似模型的RLS估计可以更加快速、准确地对光纤陀螺进行在线标定，从而为导航解算提供更加准确的光纤陀螺误差软件补偿参数.

对于使用参数辨识法进行初始对准的捷联惯导系统，求方位失准角初值的方法［11］为

式中，误差项εE/(ωiecos L)可用标定的陀螺误差参数进行补偿，即估算陀螺东向等效漂移:

如果陀螺零偏未经标定，εE将全部成为计算近似误差，则按照仿真实验的参数设置与仿真结果，可求得经补偿后由陀螺漂移引起的方位失准角初值参数辨识误差降低至原来的47.99%.

表1 2种方法的估计误差绝对值的均值Table 1 Comparison of estimation errors of the two methods

3 自标定算法硬件实现方法研究

光纤陀螺误差参数标定可以用于导航系统的自主校正，也可用于惯性稳定平台的初始对准与标定，或对光纤陀螺进行元件级的快速标定，因此可以设计相对独立的专用数字信号处理嵌入式系统以满足不同的应用需求.解耦RLS法的矩阵运算阶数低，因此具有易于用数字系统实现的优势.利用运算硬件模块的分时复用技术［12］，可以节省硬件资源，体现算法的工程应用优势.

3.1 RLS估计的程序编排

为实现算法，需将其整理成与离散化的程序编排形式.令式(8)中，各矩阵的元素如下:

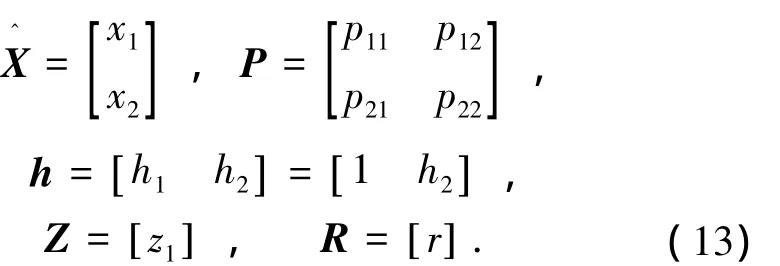
代入式(12)的递推计算公式，可以得到陀螺误差参数估计值和P矩阵的递推计算公式:

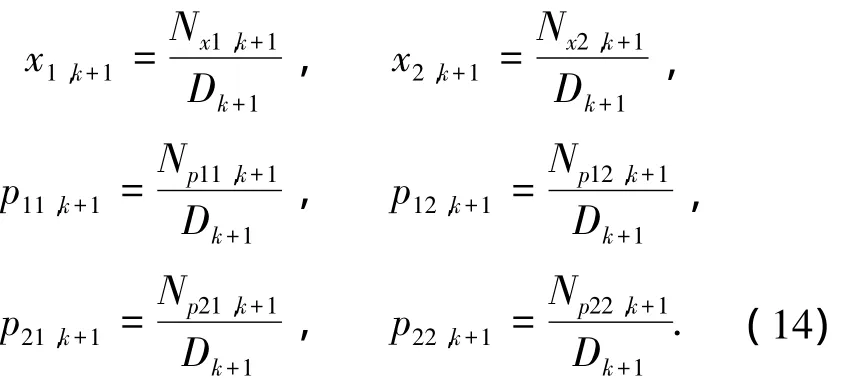
其中:

按上述解算程序迭代计算，即可实现对旋转式惯导系统IMU的光纤陀螺误差参数的RLS估计.

3.2 基于FPGA的运算电路实现

易于在结构化的硬件数字系统中实现是本文算法的特色之一.通过算法的解耦简化，最小二乘运算矩阵阶数降至二阶，提高了设计结构化逻辑电路的可行性.由于各陀螺通道最小二乘法的I/O数据格式与解算程序相同，因此可用同一运算电路分时处理三通道数据，从而节省2/3的逻辑资源.Xilinx公司的System Generator是一种结构化、模块化的FPGA开发工具，本文基于此软件工具实现基于解耦RLS的标定算法，系统的解算数据流程如图3.系统的各主要功能模块的作用和实现方法如下:

1)时序控制模块.在每个解算周期的不同时期，时序控制模块依次向数据预处理模块、数据选择模块、读写控制模块提供使能信号.

2)输入接口模块.分别采集陀螺仪、转轴角速度传感器、角位置传感器输出值，同时从导航计算机读取装订信息(载体纬度、粗对准航向角).其中陀螺输出值和角速度并行读取，而L、αx、αz在每个解算周期开始串行读取.

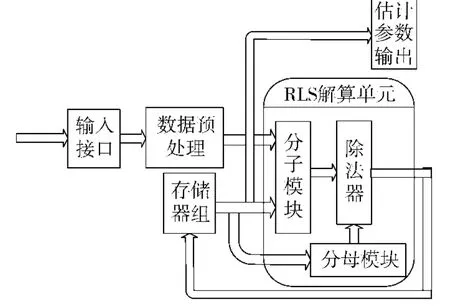
图3 RLS估计陀螺在线标定系统解算数据流图Fig.3 The computation data flow of RLS estimation based online gyro calibration system

3)数据预处理模块.每个解算周期的前100个时钟周期为数据预处理阶段，按式(7)计算各通道外观测量和观测矩阵:

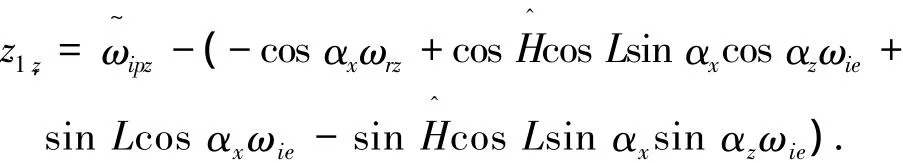
对复杂的正余弦IP核进行分时复用，串行输入L、αx、αz并用2 个时分多路开关 IP 核分别对正、余弦输出进行串并转换，可节省3/4的正余弦IP核逻辑资源.

4)数据选择模块.提供实现分时复用的多路开关［13］的控制信号:用3个多路开关分别接收预处理模块输出数据，进行并串转换，以节省逻辑资源;用1个多路开关接收RLS分子模块输出的X、P元素数据.

5)读写控制模块与存储器组模块.控制存储器组模块用6个RAM存储6个X、P矩阵元素数据以实现递推解算，与数据选择模块同步读取相应通道的x1、x2、p11、p12、p21、p22，并将除法器运算结果分别写入相应RAM的相应通道地址.在x1和x2的RAM的输出端设置外部接口，在相应的时序即可读取光纤陀螺误差参数估计值.

6)RLS解算模块组.由RLS分子、分母模块、除法器模块组成.通过多路开关将各分子参数串行输入除法器与公共的分母相除，可以节省5/6的除法器逻辑资源，得到实时的状态量估计值与P.

在System Generator开发环境下实现设计并进行仿真验证，仿真参数设置与上文仿真条件相同，而其中递推解算周期按 FPGA系统设定为0.1 ms，经过0.5 s的RLS估计(解算5 000次)，得到的光纤陀螺零偏误差参数估计值分别为0.006 249(°)/h，0.006 353(°)/h，0.009 314(°)/h，标度因数误差参 数 估 计 值 分 别 为9.065 5× 10-6，9.047 2×10-6，9.047 9×10-6.实验结果表明基于FPGA实现的解耦RLS估计数字信号处理系统可以实现对旋转IMU中光纤陀螺的零偏与标度因数误差的在线标定.

4 结论

本文通过对旋转IMU中光纤陀螺输出模型的解耦简化，建立其在线自主标定数学模型，设计了光纤陀螺零偏和标度因数误差RLS估计算法及标定方案.仿真实验表明，相对于捷联惯导静基座Kalman滤波对准方法，可提高光纤陀螺误差参数的估计精度.

利用标定参数可改善初始对准性能，对于Kalman滤波初始对准.利用标定参数进行模型降阶，可使Kalman滤波运算量降低约80%.对于参数辨识法初始对准，陀螺误差的标定值可使由陀螺漂移引起的方位失准角初值的近似误差降低50%以上.

本文算法具有易于硬件系统实现的优势，根据各陀螺通道解算程序相同的特点，利用存储器和时分多路开关实现RLS解算模块的分时复用，相关逻辑资源可以节省2/3.在外观测量初始化模块和RLS解算模块中分别对三角函数和除法器IP核分时复用，实现正余弦运算和除法运算的逻辑资源可分别节省3/4和5/6.本文基于FPGA实现了解耦RLS估计算法，为其在导航系统中的实现奠定了基础.

［1］GAO Wei，BEN Yueyan，ZHANG Xin，et al.Rapid fine strap down INS alignment method under marine mooring condition［J］.IEEE Transactions on Aerospace and Electronic Systems，2011，47(4):2887-2896.

［2］何昆鹏，许德新，吴简彤，等.船用捷联惯性导航系统在系泊状态下快速初始对准与标定［J］.哈尔滨工程大学学报，2008，29(9):944-950.HE Kunpeng，XUDexin，WU Jiantong，et al.Initial rapid alignment/calibration of amarine strap down inertial navigation system inmoorage［J］.Journal of Harbin Engineering University，2008，29(9):944-950.

［3］SUN Feng，SUN Wei，GAO Wei，et al.Research on the technology of rotational motion for FOG strapdown inertial navigation system［C］//Proceedings of IEEE International Conference on Mechatronics and Automation.Changchun，China，2009:4913-4918.

［4］BEN Yueyang，WU Xiao，CHAIYongli，et al.Research on error modulating of sin S based on sin gle-axis rotation［C］//Proceedings of International Conference on Complex Medical Engineering.Harbin，China，2011:293-297.

［5］WU Yuanxin，ZHANG Hongliang，WU Meiping，et al.Observability of strapdown INS alignment:a global perspective［J］.IEEE Transactions on Aerospace and Electronic Systems，2012，48(1):78-102.

［6］PECHT E，MINTCHEV M P.Observability analysis for INS alignment in horizontal drilling［J］.IEEE Transactions on Instrumentation and Measurement，2007，56(5):1935-1945.

［7］PECHT E，MINTCHEV M P.Modeling of Observability during in-drilling alignment for horizontal directional drilling［J］.IEEE Transactions on Instrumentation and Measurement，2007，56(5):1946-1954.

［8］LAI Jizhou，LV Pin，LIU Jianye，et al.Analysis of coning motion caused by turntable＇s vibration in rotation inertial navigation system［C］//Proceedings of IEEE/ION Position Location and Navigation Symposium.Nanjing，China，2012:869-876.

［9］陈世同，孙枫，李绪友.集成光学相位调制器相位漂移补偿方法研究［J］.哈尔滨工程大学学报，2008，29(1):45-49.CHEN Shitong，SUN Feng，LI Xuyou.Compensation for phase drift in an integrated optical phase modulator［J］.Joumal of Harbin Engineering University，2008，29(1):45-49.

［10］张国良，曾静.组合导航原理与技术［M］.西安:西安交通大学出版社，2008:150-152.ZHANG Guoliang，ZHENG Jing.Principles and technology of integration navigation［M］.Xi’an:Xi’an Jiaotong University Press，2008:150-152.

［11］秦永元.惯性导航［M］.北京:科学出版社，2006:363-373.QIN Yongyuan.Inertial navigation［M］.Beijing:Science Press，2006:363-373.

［12］RUAN Aiwu，LIAO，Yongbo，LI Ping，et al.An ALU-based universal architecture for FIR filters［C］//Proceedings of 2009 International Conference on Communications，Circuits and Systems，Milpitas，CA，2009:1070-1073.

［13］BENLACHTAR Y，WATTSPM，BOUZIANER，et al.Real-time digital signal processing for the generation of optical orthogonal frequency-division-multiplexed signals［J］.IEEE Journal of Selected Topics in Quantum Electronics，2010，16(5):1235-1244.