pq3维半单Hopf代数的结构
董井成,戴 丽
(1.东南大学 数学系,南京210096;2.南京农业大学 工学院,南京210031)
目前,关于有限维半单Hopf代数的分类研究已取得许多结果.设p,q,r是不同的素数.p维、p2维、p3维和pq维半单Hopf代数已被完全分类[1-4].特别地,Etingof等[5]用Fusion范畴的方法完成了pq2维和pqr维半单Hopf代数的分类;董井成等[6-9]给出了p2q2维和pq3维半单Hopf代数的结构和分类.文献[6]研究了pq3维半单Hopf代数的结构,其中p,q是满足条件p>q3的素数,证明了此类Hopf代数或者是半可解的,或者同构于Radford双积R#A,其中:A是q3维半单Hopf代数;R是左Yetter-Drinfeld模范畴Y D中的p维半单Hopf代数.
本文研究pq3维半单Hopf代数的结构,证明了文献[6]的结论可被推广到p>q2的情形,且本文的证明包含了文献[6]的情形.本文仅在一个特征为零的代数闭域k上讨论问题.本文所有模和余模都是k上的有限维左模和左余模,⊗k和dimk简记为⊗和dim.Hopf代数的符号和性质参见文献[10].
1 预备知识
假设T是k上的有限维半单Hopf代数.设V是一个T-模.定义V的特征标x=xV∈T*为〈x,h〉=trV(h),∀h∈T.定义x的次数为deg x=〈x,1〉=dimV.平凡T-模的特征标是余单位ε.用符号Irrt(T)表示T所有t次不可约特征标的集合,即所有t维单模的特征标.
设Irr(T)表示T所有互不同构的不可约特征标的集合,则Irr(T)可以张成T*的一个子代数[4],称为T的特征标代数,用R(T)表示.对极S可以导出一个反代数对合*:
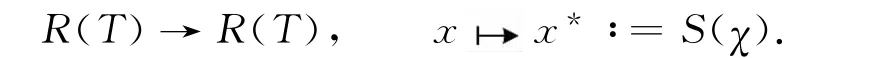
如果R(T)的子代数S可由T的不可约特征标张成,则称S为R(T)的标准子代数.因此,如果B是Irr(T)的一个子集,则B可以张成R(T)标准子代数的充分必要条件是:B中任意两个特征标的乘积仍可分解为B中特征标的和.由文献[11]中定理6的对偶情形可知,在R(T)的标准子代数与T的商Hopf代数之间存在一一对应关系.
T*的类群元集合G(T*)通过左乘(或右乘)作用在集合Irrt(T)上.任取x∈Irrt(T),记x在该作用下的稳定化子为G[x].它是G(T*)的子群,并且阶数不超过(deg x)2.特别地,g∈G[x]的充分必要条件是g在xx*的分解中,并且重数为1[11].因此,可得如下分解式
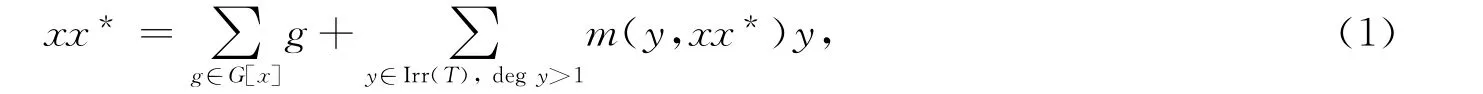
其中m(y,xx*)表示y在xx*分解中的重数.
引理1[12-13]设x是T 的不可约特征标,则:
1)x稳定化子G[x]的阶数整除(deg x)2;
2)类群元集合G(T*)的阶数整除n(deg x)2,其中n是非同构的deg x次不可约特征标的个数.
如果d1=1<d2<…<ds是所有单T-模的维数,ni是非同构的di维单T-模的个数,则称T具有代数型(d1,n1;…;ds,ns).如果对偶 Hopf代数T*具有代数型(d1,n1;…;ds,ns),则称T 具有余代数型(d1,n1;…;ds,ns).如果T 具有代数型(d1,n1;…;ds,ns),则T 同构于一组全矩阵代数的直积:

设A是有限维 Hopf代数.对于A的 Hopf子代数B,如果a1BS(a2)⊆B或S(a1)Ba2⊆B,∀a∈A,则称B是正规的Hopf子代数.如果A不含有真的正规Hopf子代数,则称其为单Hopf代数.易验证A是单Hopf代数当且仅当A*是单的.
引理2 设π:A→是余正规的商Hopf代数.假设dim是可以整除dimA的最小素数,则有

其中Z(A*)表示A*的中心.
命题1 设q是一个素数.如果T有代数型(1,q2;q,m;…),其中q不能整除m,则T*有一个维数≥2q2的Hopf子代数K,且kG(T*)是K的一个正规Hopf子代数.


设C是T*包含xq的q2维单子余代数,则

由文献[14]中命题3.2.6知,G(T*)是K∶=k[C]的正规Hopf子代数,其中k[C]表示由C生成的子代数.易验证K 是T*包含kG(T*)的 Hopf子代数.由于K 由C 生成并包含kG(T*),故dim K≥2q2.
设π:T→B是Hopf代数同态,考虑其余不变子空间:

则由文献[15]知,余不变子空间Tcoπ是T在左伴随作用下稳定的左余理想子代数,并且

综合文献[14]的1.3节可得:
引理3 设π:T→B是Hopf代数同态,A是满足条件A⊆Tcoπ的T的Hopf子代数.则dimA整除dimTcoπ.
类似于可解群的定义,可给出半可解Hopf代数的定义.如果存在一条Hopf子代数的链

则称T为下半可解的,其中对任意的i,Ti+1是Ti正规的Hopf子代数,且所有的商Hopf代数Ti/TiT+i+1都是平凡的.这里平凡的含义是指这些Hopf代数同构于群代数或对偶的群代数.如果存在一条Hopf商代数的链

由文献[16]中推论3.3可知,T是上半可解的当且仅当T*是下半可解的.此时,T可以通过多次扩张由平凡的Hopf代数构造.如果T是上半可解的或下半可解的,则称其为半可解的.
命题2[8]设T是pq3维半单Hopf代数,其中p,q是不同的素数.如果T不是单Hopf代数,则它是半可解的.
R#A具有如下性质:设T是一个有限维Hopf代数并带有Hopf代数同态ι:A→T和π:T→A.如果πι:A→A是一个Hopf代数同构,则左余理想子代数R=Tcoπ具有A 上自然的Yetter-Drinfeld Hopf代数结构,并且R#A→T可导出一个Hopf代数同构.
用D(T)=T*cop▷◁T表示T的Drinfeld偶,作为向量空间D(T)即为T*cop⊗T,是一个具有特殊结构的Hopf代数[10].由文献[19]中命题9和命题10可得:
定理1 设T是一个有限维Hopf代数,则:
2)D(T)*的每个类群元都具有形式g⊗η,其中:g∈G(T);η∈G(T*).进一步,g⊗η∈G(D(T)*)当且仅当η▷◁g在D(T)的中心内.
推论1 设T是一个有限维Hopf代数,G(D(T)*)是一个非平凡的群.如果G(D(T)*)包含元素g⊗η,其中g和η的阶数不同,则T和T*均有一个非平凡的中心类群元.特别地,T不是单Hopf代数.
证明:假设1≠g∈G(T),否则η∈G(T*)将是T*一个非平凡的中心类群元.类似地,可以假设ε≠η∈G(T*).设g的阶数是n,则

即ηn▷◁1在D(T)的中心.因此,ηn是T*一个非平凡的中心类群元.类似地,可证明T也含有一个非平凡的中心类群元.
2 主要结果

考虑分解式(2),易见当q2<p<q3时,单T-模的维数只能是1,q,q2或p,而当p>q3时,单T-模的维数只能是1,q,q2或q3.因此,可得:

其中a,b,c均为非负整数.
由 Nichols-Zoeller定理[12]知,G(T*)的阶整除dimT.
引理4 如果q2<p<q3,则G(T*)的阶数不可能是q和pq;如果p>q3,则G(T*)的阶数不可能是p,q和pq.


1)T不是单Hopf代数;
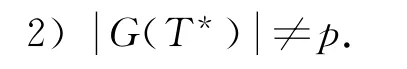
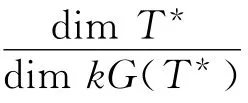
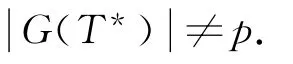

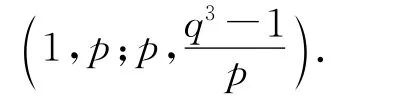
设x是一个p次不可约特征标.显然,G[x]≠{ε},否则由式(1)知,xx*的分解将会导出矛盾p2=1+mp,其中m 是某个正整数.即G[x]=G(T*).进一步,由文献[14]中引理2.1.4知,G[x*]=G(T*).因此,设C是包含x的T*的单子余代数,则由文献[14]中注3.2.7知,C/C(kG(T*))+是一个余交换的余代数.再由文献[14]中推论3.3.2知,余代数T*/T*(kG(T*))+是余交换的.


命题3 设T具有代数型(1,q2;q,m;…)且q不整除m,则:
1)如果T具有余代数型(1,q2;q,n;…)且q不整除n,则T或者不是单的,或者同构于Radford双积R#A,其中A是q3维的非平凡自对偶半单Hopf代数;
3)如果p≠1(mod q),则T不是单Hopf代数.
证明:由命题1,T*有一个维数≥2q2的Hopf子代数K,且K包含kG(T*)作为其正规Hopf子代数.根据 Nichols-Zoeller定理[12]dim K 整除dimT*,故dim K=pq3,pq2或q3.
如果dim K=pq3,则K=T*.由于kG(T*)在T*中是正规的,故T*不是单Hopf代数,从而T不是单Hopf代数.如果dim K=pq2,则由文献[21]中主要结论知T*也不是单Hopf代数.如果dim K=q3,则K 具有余代数型(1,q2;q,q-1).
下面考虑由包含关系K⊆T*导出的Hopf代数同态π:T→K*.由dim Tcoπ=p,如果存在1≠g∈G(T)满足g∈Tcoπ,则群代数k〈g〉包含在Tcoπ中,其中〈g〉表示由g生成的循环群.这是因为Tcoπ是T的子代数,其中元素的乘积具有封闭性.由于dimk〈g〉不整除dim Tcoπ,故与引理3矛盾.因此,作为T的左余理想,有分解:

其中Ui,Vj和Wk分别是T的q维,q2维和q3维不可约左余理想.当q2<p<q3时式(5)中的Wk不存在.
1)如果T具有给定的余代数型,则T或者不是单Hopf代数,或者有一个q3维的Hopf子代数A,且A 具有余代数型(1,q2;q,q-1).
一方面,根据A和Tcoπ分解成不可约左余理想直和的分解式,有

其中n是非负整数.另一方面,由文献[14]中引理1.3.4知,

因此,n=0,A∩Tcoπ=k1.从而π:A→ K*是一个 Hopf代数同构.由 Radford投射定理[18],T≅Tcoπ#A是一个Radford双积.由同构及A和K的余代数型知,A是非平凡的.因此,A是自对偶的,并且是文献[3]中构造的某个半单Hopf代数.
2)通过分析易得kG(T)∩Tcoπ=k1.因此,作为Hopf代数,kG(T)同构于K*.于是,由Radford投射定理[18]知,T≅R#kG(T)是一个Radford双积.
3)如果p≠1(mod q),则分解式(5)不可能成立,因而T不是单Hopf代数.

1)T或者不是单Hopf代数,或者同构于Radford双积R#A,其中A是q3维的半单Hopf代数;
2)如果p≠1(mod q),则T不是单Hopf代数.
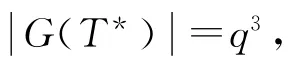
综上,本文在p>q2的假设下考察了G(T*)的每个可能阶数.因此结合命题2,可得本文的主要结果:
定理2 设T是一个pq3维半单Hopf代数,其中p,q是满足条件p>q2的素数,则T或者是半可解的,或者同构于Radford双积R#A,其中:A是q3维半单Hopf代数;R是左Yetter-Drinfeld模范畴Y D中的p维半单Hopf代数.
[1]Etingof P,Gelaki S.Semisimple Hopf Algebras of Dimension pq Are Trivial[J].Journal of Algebra,1998,210(2):664-669.
[2]Masuoka A.The pnTheorem for Semisimple Hopf Algebras [J].Proceeding of the American Mathematical Society,1996,124(3):735-737.
[3]Masuoka A.Self-dual Hopf Algebras of Dimension p3Obtained by Extension [J].Journal of Algebra,1995,178(3):791-806.
[4]ZHU Yong-chang.Hopf Algebras of Prime Dimension[J].International Mathematical Research Notices,1994,1994(1):53-59.
[5]Etingof P,Nikshych D,Ostrik V.Weakly Group-Theoretical and Solvable Fusion Categories[J].Advance in Mathematics,2011,226(1):176-505.
[6]DONG Jing-cheng.Structure Theorems for Semisimple Hopf Algebras of Dimension pq3[J].Communications in Algebra,2012,40(12):4673-4678.
[7]DONG Jing-cheng,DAI Li.Further Results on Semisimple Hopf Algebras of Dimension p2q2[J].Revista de la Unión Matemática Argentina,2012,53(2):97-112.
[8]DONG Jing-cheng,WANG Shuan-hong.On Semisimple Hopf Algebras of Dimension 2q3[J].Journal of Algebra,2013,375(1):97-108.
[9]DONG Jing-cheng.Structure of Semisimple Hopf Algebras of Dimension p2q2[J].Communications in Algebra,2012,40(3):795-806.
[10]Montgomery S.Hopf Algebras and Their Actions on Rings[M].Providence:American Mathematical Society,1993.
[11]Nichols W D,Richmond M B.The Grothendieck Group of a Hopf Algebra[J].Journal of Pure and Applied Algebra,1996,106(3):297-306.
[12]Nichols W D,Zoelle M B.A Hopf Algebra Freeness Theorem [J].American Journal of Mathematics,1989,111(2):381-385.
[13]Padres P M.On Semisimple Hopf Algebras of Dimension pq2[J].Journal of Algebra,1999,221(1):242-278.
[14]Natale S.Semisolvability of Semisimple Hopf Algebras of Low Dimension [M].Providence:American Mathematical Society,2007.
[15]Schneider H J.Normal Basis and Transitivity of Crossed Products for Hopf Algebras[J].Journal of Algebra,1992,152(2):289-312.
[16]Montgomery S,Whiterspoon S J.Irreducible Representations of Crossed Products [J].Journal of Pure and Applied Algebra,1998,129(3):315-326.
[17]Sommerhäuser Y.Yetter-Drinfeld Hopf Algebras over Groups of Prime Order [M].Lectures Notes in Mathematics,1789.Berlin:Springer-Verlag,2002.
[18]Radford D.The Structure of Hopf Algebras with a Projection[J].Journal of Algebra,1985,92(2):322-347.
[19]Radford D.Minimal Quasitriangular Hopf Algebras[J].Journal of Algebra,1993,157(2):285-315.
[20]Kaplansky I.Bialgebras[M].Chicago:University of Chicago Press,1975.
[21]Kobayashi T,Masuoka A.A Result Extended from Groups to Hopf Algebras[J].Tsukuba J Math,1997,21(1):55-58.

