随机SIQS传染病系统的灭绝性和遍历性
赵亚男,王 宇,夏 兰,张晓颖
(1.长春大学 理学院,长春130022;2.长春汽车经济技术开发区第四中学,长春130011;3.吉林交通职业技术学院 基础部,长春130012)
0 引 言
流行病动力学通过疾病内在规律的分析预测疾病的发展趋势,给出最优控制策略.当种群中存在传染病时,经典的传染病模型(SIS模型)引入隔离后,总种群(N)分为易感个体组成的子种群(S)、已染病但未隔离个体组成的子种群(I)和已染病并被隔离个体组成的子种群(Q)三类.设被隔离者恢复后也不具有免疫力,此时相应的传染病模型称为SIQS模型.具有隔离项的传染病模型[1]为
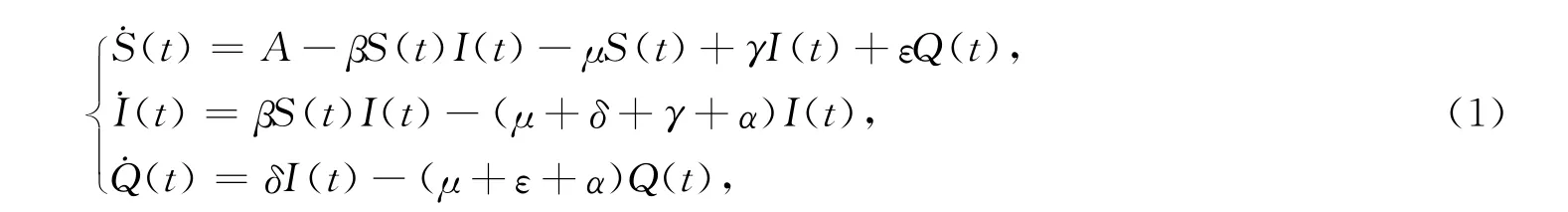
其中:A,μ,β是正常数;γ,ε,δ和α是非负常数;A是单位时间内因出生和移民而进入易感染者S类的数量,简称输入率;μ是死亡率系数;β是双线性疾病发生率系数;γ和ε分别是从染病者类I和隔离者类Q到易感类的恢复系数;δ是隔离率系数;α是因病死亡率系数.系统(1)的基本再生数是R0=Aβ/(μ(γ+δ+μ+α)).
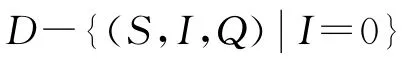
目前,研究随机传染病模型多数都引入参数扰动[2-4],通过给出平衡点附近的渐近行为反映疾病的灭绝与流行.文献[5]则通过对整个系统加入随机扰动的方法研究随机传染病模型,并分析得到了即使确定性系统各变量是持久的,而随机系统却终将灭亡.
本文采用类似于文献[5]的方法,通过对系统引入白噪声干扰,得
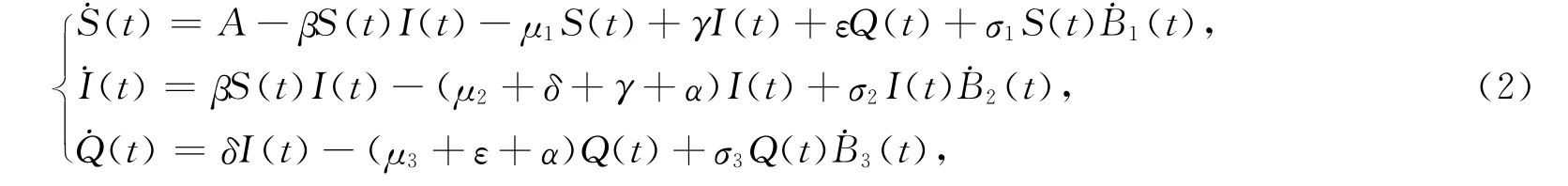
其中:Bi(t)(t≥0)是独立的标准Brown运动;表示白噪声的强度;i=1,2,3.系统(2)一般不存在无病平衡点和有病平衡点.本文主要探讨随机系统在相应确定性系统平衡点附近的动力学行为,在一定程度上反映疾病的流行与消失.当随机系统的扩散项是非退化情形时,给出系统存在平稳分布,具有遍历性.
设X(t)是El(l维Euclid空间)中的一个自治Markov过程,可表示为随机微分方程

假设条件:
(H1)存在具有正则边界Γ的有界区域U⊂El,具有如下性质:
1)在U及其一些邻域内,扩散阵Λ(x)的最小特征值是非零的;



1 正解的存在性和唯一性
定理1 对于任意给定的初值Y(0)=(S(0),I(0),Q(0))∈ ℝ3+,系统(2)存在唯一的解Y(t)=(S(t),I(t),Q(t)),t≥0,并且该解以概率1位于ℝ3+中.
证明:系统(2)的系数显然满足局部Lipschitz条件,从而系统(2)存在唯一的局部解Y(t)(t∈[0,τe)),其中τe是爆破时间[7].设k0足够大,使得Y(0)的每个分量都落在区间[1/k0,k0]中.设整数k≥k0,定义停时



由伊藤公式可得

其中
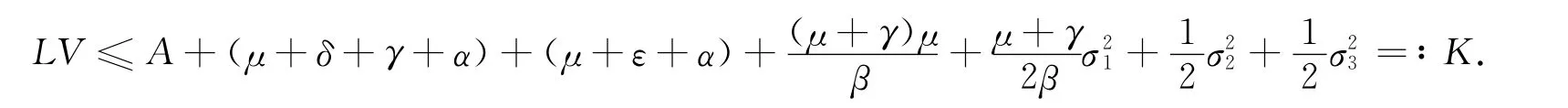
用与文献[8]类似的方法可证结果成立.
2 系统(2)在无病平衡点P0附近的渐近行为
定理2 若R0≤1,且满足假设条件(H2),则系统(2)满足初值为Y(0)∈ℝ3+的解Y(t)具有性质:
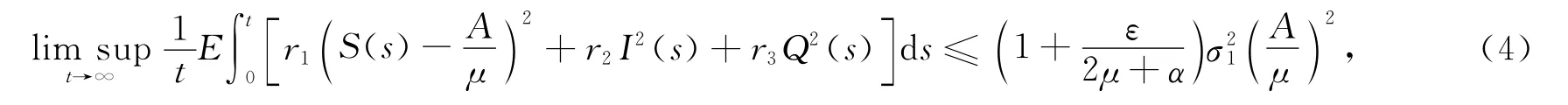
其中:

证明:令x=S-A/μ.定义V:ℝ3+→ ℝ+,

其中

是正常数.利用伊藤公式,可得

其中

当满足条件(H2)时,有r1,r2,r3>0.将式(6)从0到t积分,并对等式两边取数学期望,可得
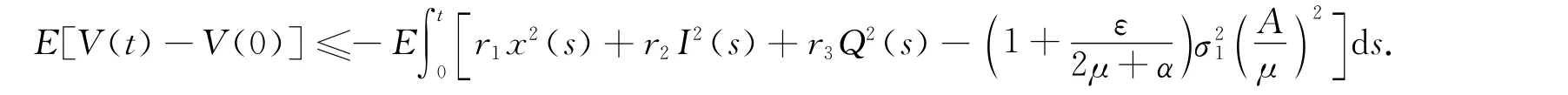
注1 定理2表明,当白噪声的强度足够小时,系统(2)的解会围绕系统(1)的无病平衡点震动,且震动大小正比于的大小.即S受白噪声影响越小,系统(2)的解越接近系统(1)的无病平衡点.
3 系统(2)的遍历性
定理3 若R0>1,且满足条件(H2)及

则对任意的初值Y(0)∈ℝ3+,系统(2)存在不变分布μ(·),且是遍历的.其中
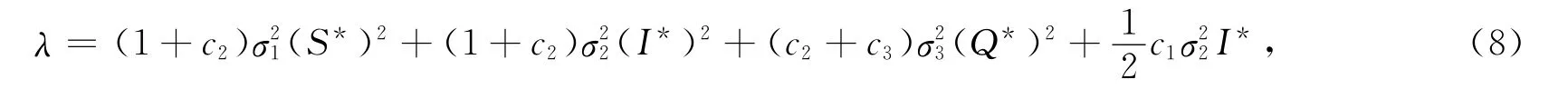
这里r1,r2,r3如定理2中定义,c1,c2,c3如式(5)定义.
证明:定义V:ℝ3+→ℝ+,

利用伊藤公式,可得

其中

这里λ如式(8)定义.由于条件(7)成立,因此椭圆-r1(S-S*)2-r2(I-I*)2-r3(Q-Q*)2+λ=0全部位于ℝ3+中.取U为包含椭圆的邻域,使得⊆El=ℝ3+,且当x∈ℝ3+\U时,LV≤-K(K是一个正常数),表明假设条件(H1)中2)满足.另一方面,存在使得对所有的(S,I,Q,)∈¯U,ξ∈ℝ3,有表明假设条件(H1)中1)满足.因此,随机系统(2)存在平稳分布μ(·),且是遍历的.证毕.
[1]Herbert H,Ma Z,Liao S.Effects of Quarantine in Six Endemic Models for Infectious Diseases[J].Mathematical Biosciences,2002,180:141-160.
[2]ZHAO Ya-nan,JIANG Da-qing,O’Regan D.The Extinction and Persistence of the Stochastic SIS Epidemic Model with Vaccination[J].Physica A,2013,392(20):4916-4927.
[3]Gray A,Greenhalgh D,Hu L,et al.A Stochastic Differential Equation SIS Epidemic Model[J].Siam J Appl Math,2011,71:876-902.
[4]ZHAO Ya-nan,JIANG Da-qing.Dynamics of Stochastically Perturbed SISEpidemic Model with Vaccination[J].Abstract and Applied Analysis,2013,2013:1-12.
[5]Imhof L,Walcher S.Exclusion and Persistence in Deterministic and Stochastic Chemostat Models [J].J Differential Equations,2005,217:26-53.
[6]Has’minskii R Z.Stochastic Stability of Differential Equations[M].Amsterdam:Sijthoff & Noordhoff,Alphen aan Den Rijn,1980.
[7]MAO Xue-rong.Stochastic Differential Equations and Applications[M].Chichester:Horwood Publishing,1997.
[8]MAO Xue-rong,Marion G,Renshaw E.Environmental Brownian Noise Suppresses Explosions in Population Dynamics[J].Stochastic Process Appl,2002,97(1):95-110.

