三维 Gel’fand-Dorfman双代数分类
祁江艳,张 钰,赵秀秀,张庆成
(东北师范大学 数学与统计学院,长春130024)
0 引言及预备知识
分类问题在代数学中应用广泛,目前已有许多研究结果,如Jacobson[1]给出了低维Lie代数的分类;Osborn[2]命名了Novikov代数,应用于Poisson结构和Hamiltonian算子中;白承铭等[3]给出了低维Novikov代数的分类;文献[4-5]给出了Novikov超代数的低维分类及一些重要性质.Gel’fand-Dorfman双代数与Hamilton对联系紧密,Gel’fand-Dorfman双代数是由Lie代数和Novikov代数在满足相容性条件下组成的,它符合某个Hamilton对[6].在量子群理论中,二次和三次共型代数、顶点算子理论及计算机组合编码中应用广泛[7-11].对于Gel’fand-Dorfman双代数的结构,白承铭等[12]已经给出了二维Gel’fand-Dorfman双代数的分类.由于三维Novikov代数的种类繁多、验证情况复杂,目前尚未见三维Gel’fand-Dorfman双代数的完全分类报道.本文给出它的完全分类.
本文所涉及的向量空间和代数均指在复数域ℂ上.
定义1 设L是域ℂ上的向量空间,且L中有一个双线性运算L×L→L,(x,y)→[x,y],如果满足下列两个条件:

则称L为域ℂ上的一个Lie代数.
定义2[2]A是域ℂ上的向量空间,在A上定义双线性积(x,y)→x◦y,如果满足下列3个条件:
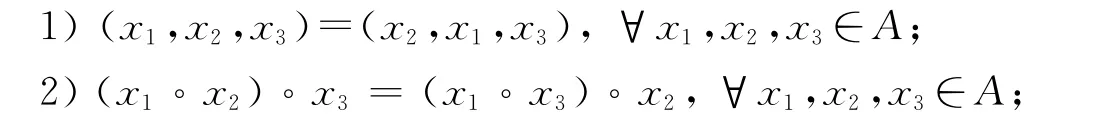

则称A是一个Novikov代数.
定义3[6]若(V,[·,·])构成一个Lie代数,(V,o)构成一个 Novikov代数,如果Lie代数和Novikov代数满足相容性条件:

则称双代数结构 (V,[·,·],o)是 Gel’fand-Dorfman双代数.
文献[1]和文献[3]分别给出了三维Lie代数和三维 Novikov代数的分类.设Li(i=1,2,…,5)表示三维Lie代数的分类;Aj,Bk,Cl,Dm,E1(j=1,2,…,13;k=1,2,…,5;l=1,2,…,19;m=1,2,…,6)表示三维Novikov代数的分类.
1 主要结果
本文给出的三维Novikov代数的分类结果均是在去除同构情况下得到的.设e1,e2,e3为Lie代数的一组基.用o1,o2,o3,o4,o5,o6分别表示 Novikov代数对应于Lie代数基底的轮换:

定理1 由L1与任一Novikov代数组成的代数约定为第一类Gel’fand-Dorfman双代数.
证明:因为L1中任意两个基元素作用均为0,因此L1与任意一类Novikov代数都满足式(1).例如:当ω=e1,μ=e2,ν=e3时,式(1)成立.
定理2 将(Li,A1)(i=2,3,4,5)约定为第二类 Gel’fand-Dorfman双代数.
证明:A1类Novikov代数中任意两个基元素作用均为0,故Li与A1都满足式(1),证毕.
定理3 (L2,A)类型Gel’fand-Dorfman双代数G的分类结果如下:

证明:首先考虑基底之间的轮换,共有o1,o2,o3,o4,o5,o66种.然后对每种情况验证是否满足式(1).若满足式(1),则为Gel’fand-Dorfman双代数;若不满足式(1),则不是 Gel’fand-Dorfman双代数.最后采用待定系数法并结合Lie代数的自同构验证找出的Gel’fand-Dorfman双代数的同构性.由于证明中演算过程过于繁多复杂,故本文只举一个例子,其他情况类似.
以(L2,A2)为例.由文献[1,3]知,
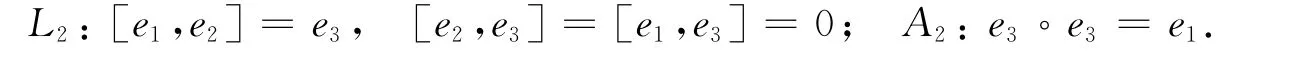
在(L2,A2,o1)中,当ω=e3,μ=e1,ν=e2时,
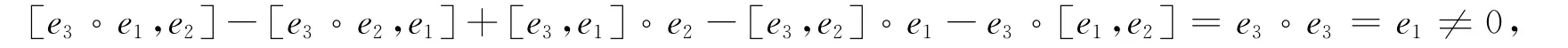
所以它 不 是 Gel’fand-Dorfman 双 代 数;在 (L2,A2,o2)中,当 ω,μ,ν 分 别 取ei,ej,ek所 有 排 列(共3×3×3=27种情况)时,式(1)均成立,所以它是Gel’fand-Dorfman双代数.同理可验证其余4种情况,可知(L2,A2,o3)不是 Gel’fand-Dorfman双代数,而(L2,A2,o4),(L2,A2,o5),(L2,A2,o6)均是Gel’fand-Dorfman双代数.最后,利用Lie代数L2的自同构易证明:(L2,A2,o2)与(L2,A2,o3)同构;(L2,A2,o5)与(L2,A2,o6)同构;(L2,A2,o2)与(L2,A2,o5)不同构.所以(L2,A2,o2)与(L2,A2,o5)是Gel’fand-Dorfman双代数.证毕.
同理可证下列定理.
定理4 (L2,C)类型Gel’fand-Dorfman双代数G的分类结果如下:

注1 当l=l1时,(L2,C13,o2)与(L2,C13,o4)同构.
定理5 (L2,D)类型Gel’fand-Dorfman双代数G的分类结果如下:
1)(L2,D2,o2);2)(L2,D3,o2);3)(L2,D3,o4).
定理6 (L3,A)类型Gel’fand-Dorfman双代数G的分类结果如下:
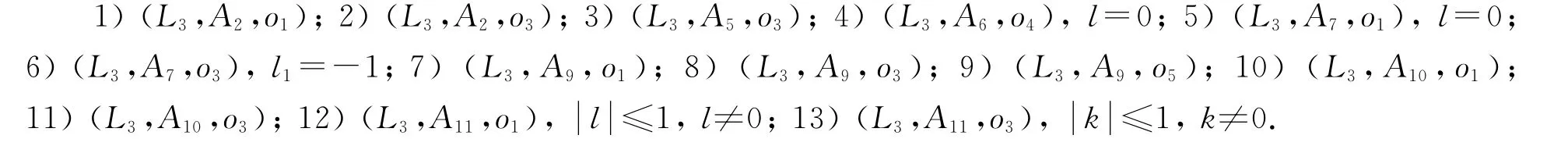
注2 当l=k=1时,(L3,A11,o1)与(L3,A11,o3)同构.
定理7 (L3,B)类型Gel’fand-Dorfman双代数G的分类结果如下:
1)(L3,B2,o1);2)(L3,B3,o1);3)(L3,B4,o1);4)(L3,B5,o1).
定理8 (L3,C)类型Gel’fand-Dorfman双代数G的分类结果如下:
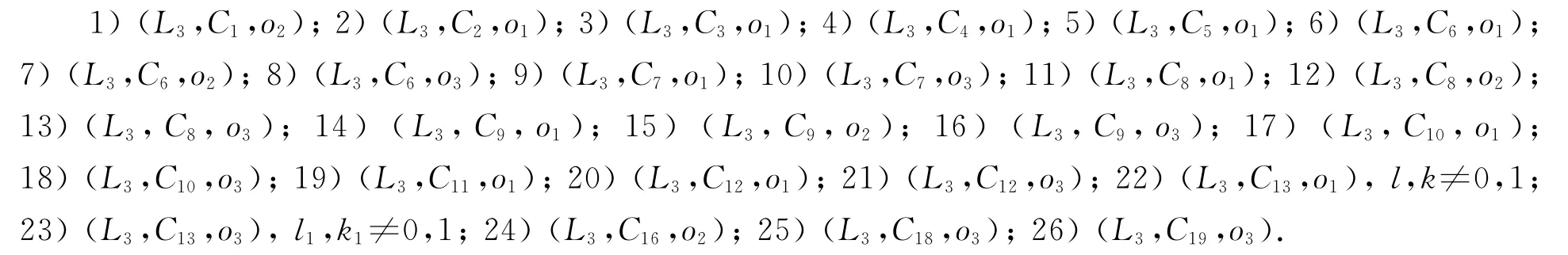
注3 当l=l1,k=k1时,(L3,C13,o1)与(L3,C13,o3)同构.
定理9 (L3,D)类型Gel’fand-Dorfman双代数G的分类结果如下:

定理10 (L3,E)类型 Gel’fand-Dorfman双代数G 的分类结果为(L3,E1,o2).
定理11 (L4,A)类型Gel’fand-Dorfman双代数G的分类结果如下:
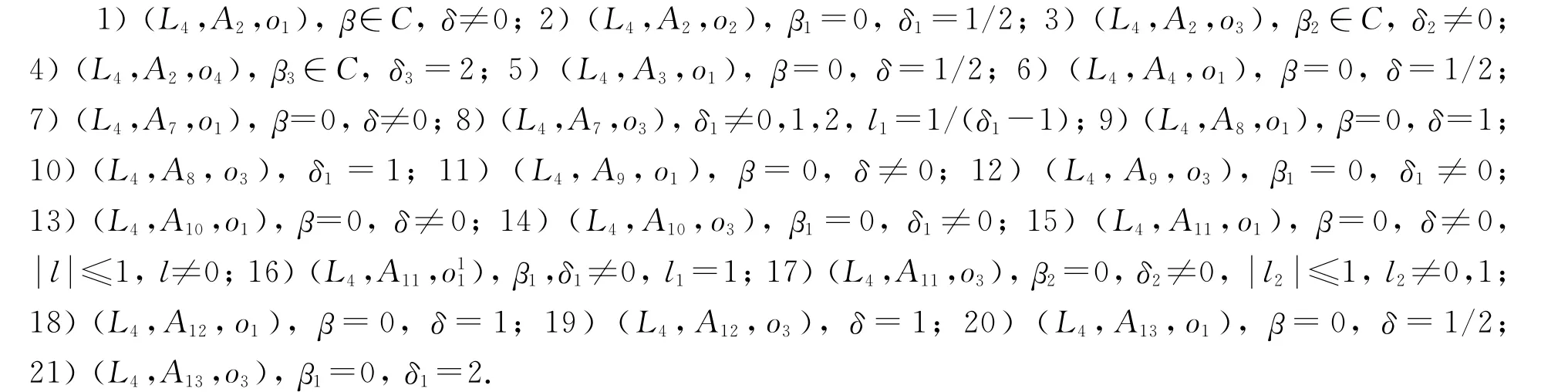
注4 当β=β2=0,δ=δ2=1或β=0,δδ2=1,δ2≠1时,(L4,A2,o1)和(L4,A2,o3)同构;当δδ1=1,l=l1时,(L4,A7,o1)和(L4,A7,o3)同构;当β1=0时,(L4,A7,o3)和(L4,A8,o1)同构;当δ=δ1=1时,(L4,A9,o1)和(L4,A9,o3)同构;当δ=δ1=1时,(L4,A10,o1)和(L4,A10,o3)同构;当l=1,δ=δ1≠1时,(L4,A11,o1)和(L4,A11,o11)同构;当δ=δ2=1,l=l2时,(L4,A11,o1)和(L4,A11,o3)同构;当β1=0时,(L4,A12,o1)和(L4,A12,o3)同构.
定理12 (L4,C)类型Gel’fand-Dorfman双代数G的分类结果如下:
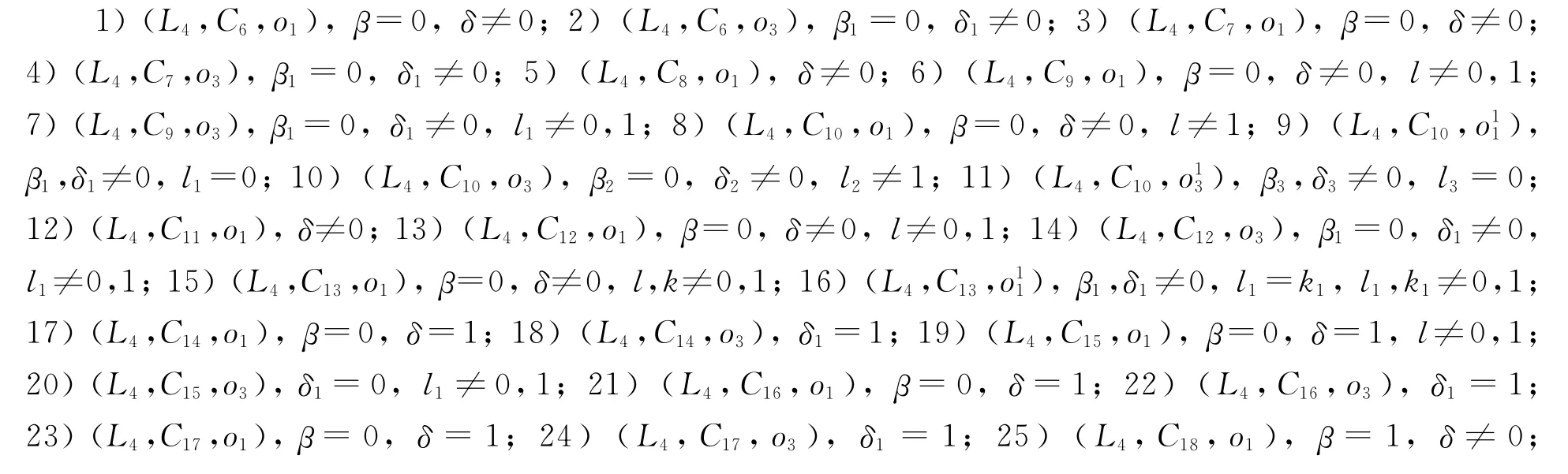

注5 当δ=δ1=1时,(L4,C6,o1)和(L4,C6,o3)同构;当δ=δ1=1时,(L4,C7,o1)和(L4,C7,o3)同构;当δ=δ1=1,l=l1时,(L4,C9,o1)和(L4,C9,o3)同构;当l=0,δ=δ1≠1时,(L4,C10,o1)和(L4,C10,o11)同构;当δ=δ2=1,l=l2时,(L4,C10,o1)和(L4,C10,o3)同构;当δ=δ1=1,l=l1时,(L4,C12,o1)和(L4,C12,o3)同构;当l=k=l1,δ=δ1≠1时,(L4,C13,o1)和(L4,C13,o11)同构;当β1=0时,(L4,C14,o1)和(L4,C14,o3)同构;当β1=0,l=l1时,(L4,C15,o1)和(L4,C15,o3)同构;当β=0时,(L4,C16,o1)和(L4,C16,o3)同构;当β=0时,(L4,C17,o1)和(L4,C17,o3)同构.
定理13 (L4,D)类型Gel’fand-Dorfman双代数G的分类结果如下:
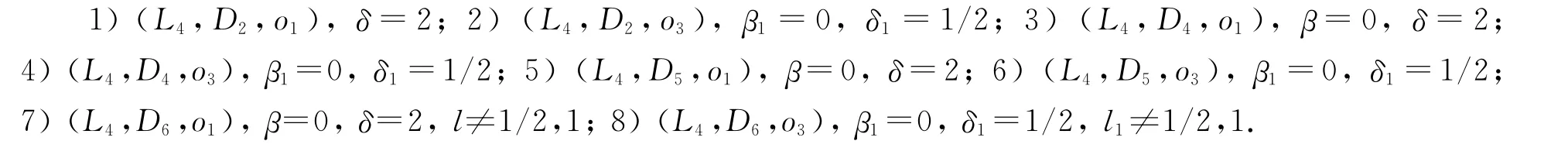
[1]Jacobson N.Lie Algebras[M].New York:Interscience-Wiley,1962.
[2]Osborn J.Novikov Algebras[J].Nova J Algebra Geom,1992(1):1-14.
[3]BAI Cheng-ming,MENG Dao-ji.The Classification of Novikov Algebras in Low Dimensions[J].J Phys A:Math Gen,2001,34(8):1581-1594.
[4]KANG Yi-fang,CHEN Zhi-qi.Novikov Superalgebras in Low Dimensions[J].J Nonlinear Math Phys,2009,16:251-257.
[5]ZHU Fu-hai,CHEN Zhi-qi.Novikov Superalgebras with A0=A1A1[J].Cze Math J,2010,60(4):903-907.
[6]Gel’fand I M,Dorfman Y I.Hamiltonian Operators and Algebraic Structures Related to Them [J].Funkts Anal Its Prilozhen,1979,13(4):248-262.
[7]XU Xiao-ping.Quadratie Conformal Superalgebras[J].J Algebra,2000,231(1):1-38.
[8]XU Li-yuan,ZHANG Qing-cheng,MENG Dao-ji.Some Properties of Tortken Superalgebras and Classification of Low Dimensional Tortken Superalgebras[J].Acta Mathematica Scientia,2011,31A(5):1190-1208.(徐丽媛,张庆成,孟道骥.低维Tortken超代数的分类与Tortken超代数的一些性质 [J].数学物理学报,2011,31A(5):1190-1208.)
[9]ZHANG Qing-cheng,ZHANG Shuang.The Homology and Cohomology of Generalized Poisson Superalgebra[J].Chinese Annals of Mathematics,2011,32A(3):257-266.(张庆成,张爽.广义Poisson超代数的同调与上同调群 [J].数学年刊,2011,32A(3):257-266.)
[10]JIA Zhi-peng,ZHANG Qing-cheng.Nilpotent Ideals of Lie Color Triple Systems[J].Journal of Jilin University:Science Edition,2011,49(4):674-678.(贾志鹏,张庆成.李 Color三系的幂零理想 [J].吉林大学学报:理学版,2011,49(4):674-678.)
[11]ZHANG Qing-cheng,ZHANG Xiao-dong,WEI Zhu,et al.Some Identities of Associative Lie Color Algebras and P-Solvable Restricted Lie Color Algebras[J].Acta Mathematica Scientia,2012,32A(3):450-467.(张庆成,张小东,魏竹,等.结合李Color代数的等式与P-可解限制李Color代数 [J].数学物理学报,2012,32A(3):450-467.)
[12]BAI Cheng-ming,MENG Dao-ji.The Automorphisms of Novikov Algebras in Low Dimensions[J].J Phys A:Math Gen,2003,36(28):7715-7731.

