具非标准增长条件和正初始能量的非牛顿多方渗流方程解的爆破
刘 令,王国铭,谢嘉宁
(1.吉林建筑大学 基础科学部,长春130118;2.吉林大学 数学学院,长春130012;3.东北财经大学 数学与数量经济学院,辽宁 大连116025)
0 引 言
考虑如下初边值问题:


为方便,引进如下符号:

这里

设Lr(·)(Ω)表示如下可测函数空间:

其范数为
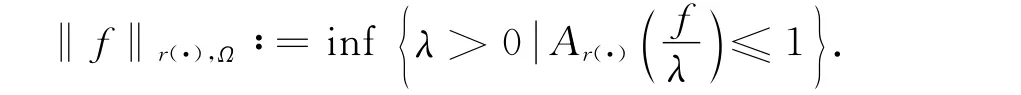
易验证Lr(·)(Ω)是Banach空间[4,6].由范数定义有

根据文献[4,6]可知

令B1=max{B,m1/p}.定义

则

1 引 理
引理1 函数E(t)关于时间变量t是非增的.
证明:由问题(1)及式(8),对函数E(t)求导得
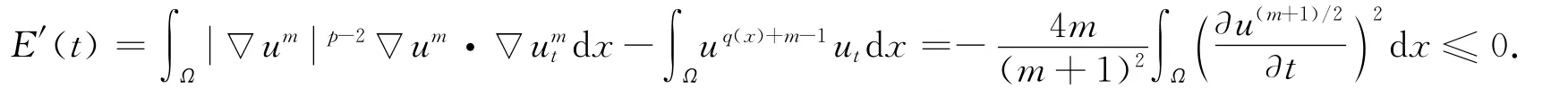
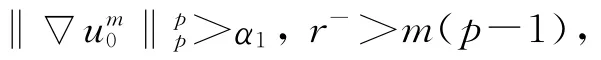

证明:由式(5),(8)有
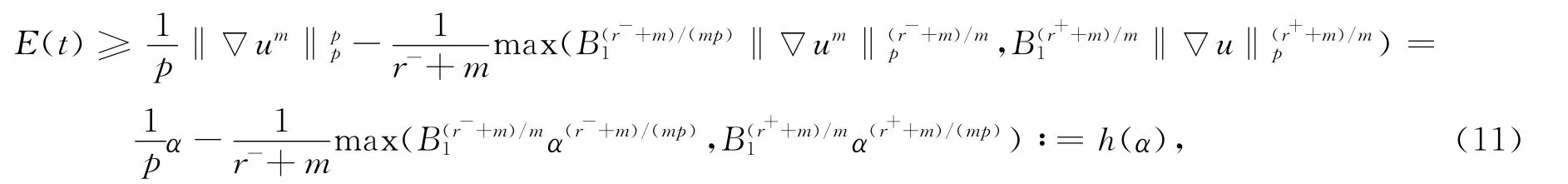
其中α=‖▽um‖.易验证h(α)在区间(0,α1)上单调递增,在区间(α1,+∞)上单调递减且h(α)→-∞,当α→+∞时,h(α1)=E1,其中E1,α1的定义如式(6),(7).由于E(0)<E1,故存在α2>α1,使得h(α2)=E(0).令α0=‖▽‖,由式(11)有h(α0)≤E(0)=h(α2),进一步还可证明α0≥α2.
假设式(9)不成立,即存在t0>0,使得‖▽um(·,t0)‖<α2.由于‖▽um(·,t)‖关于时间t连续,故可选取t1>0,使得‖▽um(·,t1)‖>α1.进一步,根据函数h(α)的单调性,有
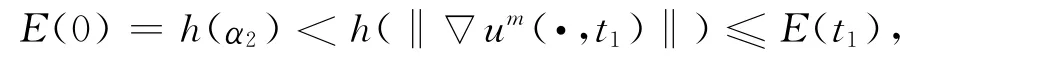
这与引理1矛盾.
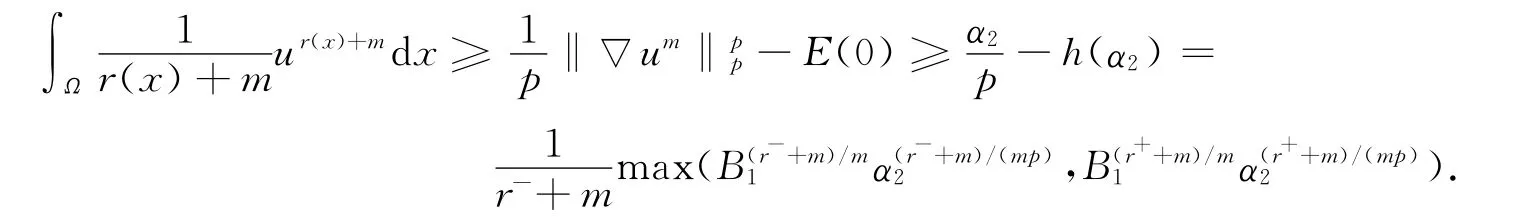
定义 H(t)=E1-E(t).
引理3 对所有t>0,均有
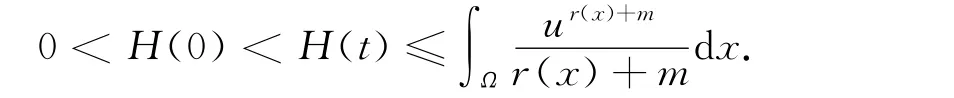
证明:由引理1,有H′(t)≥0,即 H(t)≥H(0)>0,∀t≥0.根据式(8),(11)有

2 主要结果
定理1 假设r(x)满足式(2),(3),且如下条件成立:

则问题(1)的解在有限时刻爆破.
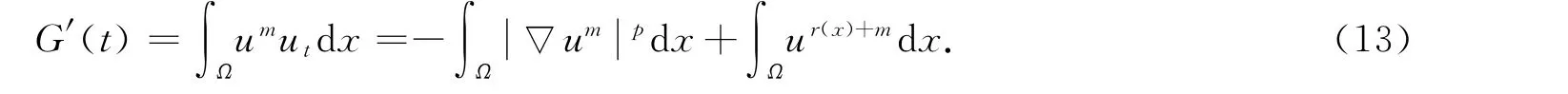
由式(8),(12),有
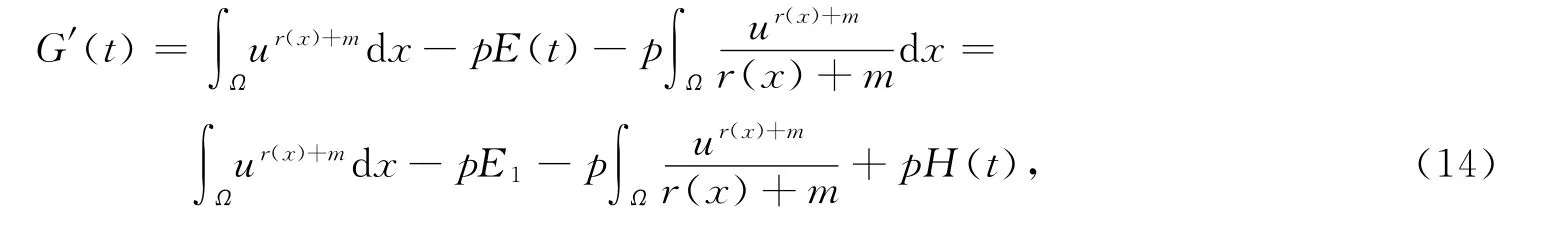
其中

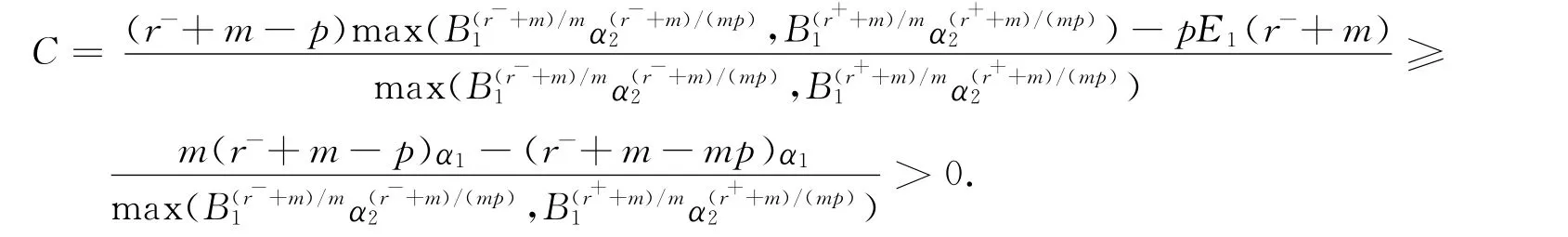
由式(4),有

由Lr(·)+m(Ω)⊂Lm+1(Ω),有

又根据式(15)~(17),有



[1]Levine H A.Some Nonexistence and Instability Theorems for Solutions of Formally Parabolic Equations of the FormPut=-Au+F(u)[J].Arch Rationale Mech Anal,1973,51(5):371-386.
[2]LIU Wen-jun,WANG Ming-xin.Blow-up of the Solution for a p-Laplacian Equation with Positive Initial Energy[J].Acta Appl Math,2008,103:141-146.
[3]Dibenedetto E.Degenerate Parabolic Equations[M].New York:Springer-Verlag,1993.
[4]Ruzicka M.Electrorheological Fluids:Modelling and Mathematical Theory [M].Lecture Notes in Math.Vol.1748.Berlin:Springer,2000.
[5]Acerbi E,Mingione G,Seregin G A.Regularity Results for Parabolic Systems Related to a Class of Non-Newtonian Fluids[J].Annal del’Institut Henri Poincare:Analyse Non-lineaire,2004,21:25-60.
[6]Diening L,Harjulehto P,Hasto P,et al.Lebesgue and Sobolev Spaces with Variable Exponents[M].Lecture Notes in Math.Vol.2017.Berlin:Springer-Verlag,2011.
[7]Ferreira R,Pablo A,de,Prez-Llanos M,et al.Critical Exponents for a Semilinear Parabolic Equation with Variable Reaction[J].Proc Roy Soc Edinburgh:Sect A,2012,142(5):1027-1042.
[8]WU Xiu-lan,GUO Bin,GAO Wen-jie.Blow-up of Solutions for a Semilinear Parabolic Equation Involving Variable Exponent Source and Positive Initial Energy[J].Appl Math Lett,2013,26(5):539-543.
[9]YIN Jing-xue,LI Jing,JIN Chun-hua.Non-extinction and Critical Exponent for a Polytropic Filtration Equation[J].Nonlinear Anal:Theory,Methods & Applications,2009,71(1/2):347-357.
[10]MU Chun-lai,ZENG Rong,CHEN Bo-tao.Blow-up Phenomena for a Doubly Degenerate Equation with Poitive Initial Energy[J].Nonlinear Anal,2010,72(2):782-793.

