铺设台阶 引人入胜——解题教学“一题一课”的实践与思考

●

(金华市教育局教研室 浙江金华 321000)

铺设台阶引人入胜
——解题教学“一题一课”的实践与思考

●傅瑞琦

(金华市教育局教研室 浙江金华 321000)

有效的例题教学，将反馈、巩固和拓展学生对所学知识的理解与记忆，是学生掌握基本知识、基本技能、基本思想方法和积累活动经验的重要途径.通过方法的渗透和体验，让学生学会用数学思想方法解决问题，使学生在思维能力、情感态度与价值观等方面得到协调发展.

但是在教学调研中发现，初三的例题教学，常常就题论题，更多关注学生求解答案的正确与否，关于难点的解决常以一种告诉的方式呈现，不能很好地体会例题中所蕴含的思维方法和思想方法,结论的得出、方法的归纳、思想的提炼没有充分暴露学生的思维，不能有效地唤醒学生已有的知识,学生就失去了在数学学习过程中发展能力、体现个性的机会.

基于此，笔者所在教研室组织了“一题一课”主题教研活动，本文结合教师2次教学实践的对比思考，探讨如何设计对学生思维有启发的、能引起学生思考和探索活动的问题来铺设台阶，有效突破难点，使思维层层深入.

1 例题选用

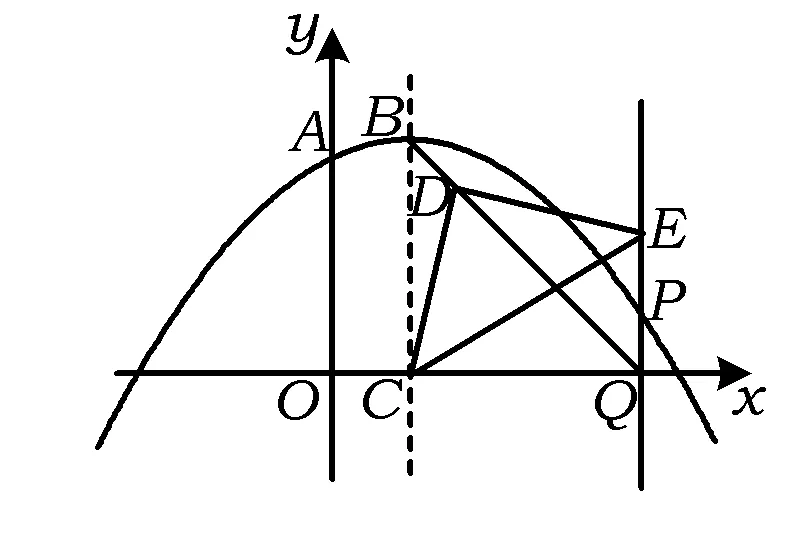
图1

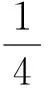
(1)若含45°角的直角三角板如图1所示放置，其中一个顶点与点C重合，直角顶点D在BQ上，另一个顶点E在PQ上．求直线BQ的函数解析式.

(2)若含30°角的直角三角板的一个顶点与点C重合，直角顶点D在直线BQ上，另一个顶点E在PQ上，求点P的坐标．

(2011年浙江省绍兴市数学中考试题改编)

2 教学过程

教学设计1

问题引导如图2，将直角三角板的直角顶点E放在正方形ABCD的顶点A上，三角板的2条直角边交CD于点F，交CB的延长线于点G，你能得到哪些结论？

生1：∠GAB=∠DAF.

生2：EG=EF，BG=DF…

师(追问)：你能说明理由吗？

生3：证明△ADF≌△ABG,就可以得出上述结论.

图2 图3 图4

变式1如图3，如果移动三角板，使顶点E始终在正方形ABCD的对角线AC上，其他条件不变,结论EG=EF是否仍然成立？请你说明理由.

生4：EG=EF仍然成立.

生5：理由是过点E作EP⊥BC,EQ⊥DC，有Rt△EGP≌Rt△EFQ(如图3)，得EG=EF.

师(小结)：通过图形对比，联想构造全等三角形，可得出结论.

变式2如图4，移动三角板，使顶点E不在正方形ABCD的对角线AC上,结论EG=EF是否仍然成立？

生6：EG与EF不相等.

师：如果过点E作EP⊥BC,EQ⊥DC，你可以得到什么结论？

生7：Rt△EGP与Rt△EFQ相似(如图4).

师(小结)：弱化条件“点E不在正方形的对角线上”，但图形的主要特征没有发生变化，过点E作2条直角边的垂线，来构造2个相似三角形，得出线段的比例关系.

反思感悟从上面的问题探究中，你能得到什么结论？

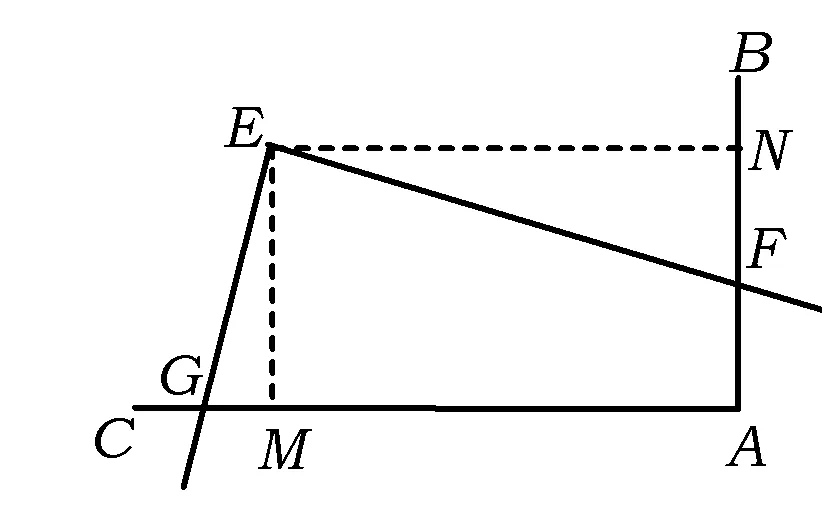
图5

生8：当2个直角对角放置时(如图5)，通常可以过一直角顶点作另一直角2边的垂线，构造2个相似(全等)三角形.

师(小结)：构造2个相似(或全等)三角形,实现问题转化.

解决例题有了图5基本图形的提炼，给出例题后学生很快就会想到添加辅助线，顺利完成解题:

(1)如图6，过点D作DM⊥x轴，DN⊥PQ，垂足为M,N，则

△DCM≌△DEN，

于是

DM=DN，

从而

∠DQO=45°，

可求得OQ=4，即Q(4，0)，故直线BQ的解析式为y=-x+4.

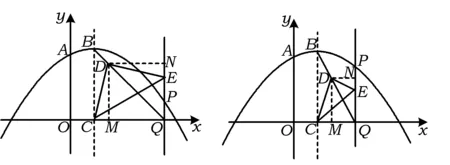
图6 图7

(2)当点P在对称轴的右侧时(如图7)，过点D作DM⊥x轴，DN⊥PQ，垂足为M,N.设点(m，0)，则

Rt△CDM∽Rt△EDN，

得

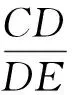
从而

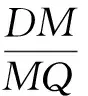
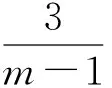
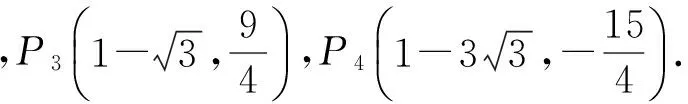
反思这节课，其教学过程是“创设问题情境，构造基本图形，寻求解题思路”，设计了问题引导及2个变式的台阶，降低思维坡度，学生顺利添加辅助线，完成解题.

但是，从课堂观察看，学生都千篇一律地用图5作垂线的方法构造全等(相似)三角形来解题，这引发教师的反思，为什么学生解题方法单一，不会寻求另外的解法？基本图形的构造是学生的难点，“台阶”的设置让学生顺利突破难点，是否太顺利了？

于是笔者所在教研室组织了教师研讨，对本节课的教学任务、教学目标、示例功能及教学效果等方面进行探讨、分析.

教学任务这2个小题的共同之处是图形特征相同，其区别是三角板摆放位置的不同和内角度数的不同.第(2)小题对30°角分类学生容易想到，但第(1)小题求解时需要添加辅助线，来说明∠BQO=∠CED，对数学感知能力要求较高，是本题的难点.如何突破该难点，教学时需要根据图形特点，设计问题引导，铺设思维台阶，引导学生有效思考.

教学目标理解有几何图形背景问题的思考方法，利用三角形相似(全等)性质、函数基本性质，以及应用数形结合、函数与方程等数学思想方法来解决问题；培养学生运用动态图形进行分析、解决问题的能力，增强用分类讨论、转化归纳来分析解决问题的意识；体会提炼基本图形，感受方程的应用价值，提高根据题意解决问题的缜密思考的习惯.

本课例一开始就以一种告诉的形式呈现2个三角形全等的图形，问题指向狭窄，学生只是进行机械模仿，易形成思维定势，束缚了学生的思维，没有达到教学目标.

示例功能本题是函数背景下常见的动态综合题型,重点考查学生的数学思想方法及综合应用能力.2个小题中均隐含着不变的因素，即∠BQO=∠CED，如何说明这2个角相等是解决该题的关键.通过本题，引导学生学会独立思考，根据图形特征、符号特征等信息，来联系相关数学知识，添加辅助线，充分经历数学活动过程，训练学生的几何直觉，在探究中培育思维品质，积累解题经验.

教学效果通过该例的思考解决，能真正体现例题的思维价值，使学生能举一反三、触类旁通.

基于这些思考，上课教师着手修改，以教学设计2来组织教学.

教学设计2

(1)创设问题情境，引导探究.

在直角坐标系中，将直角三角板OPE如图8所示放置，45°角的顶点在原点，过点E作EQ⊥x轴，Q为垂足，联结QP交y轴于点D,你能够得出什么结论？并能说明理由.

学生思考5分钟后,教师要求进行小组交流，并呈现问题串:

问题1如果你还没有得出满意的结论，是否可以把三角板放到特殊位置再思考？

问题2你可以画出哪些特殊位置，结论是什么？

问题3你猜测的结论，在一般情况下是否还成立？试旋转三角板，判断你的结论.

问题4如果成立，你能够说明理由吗？

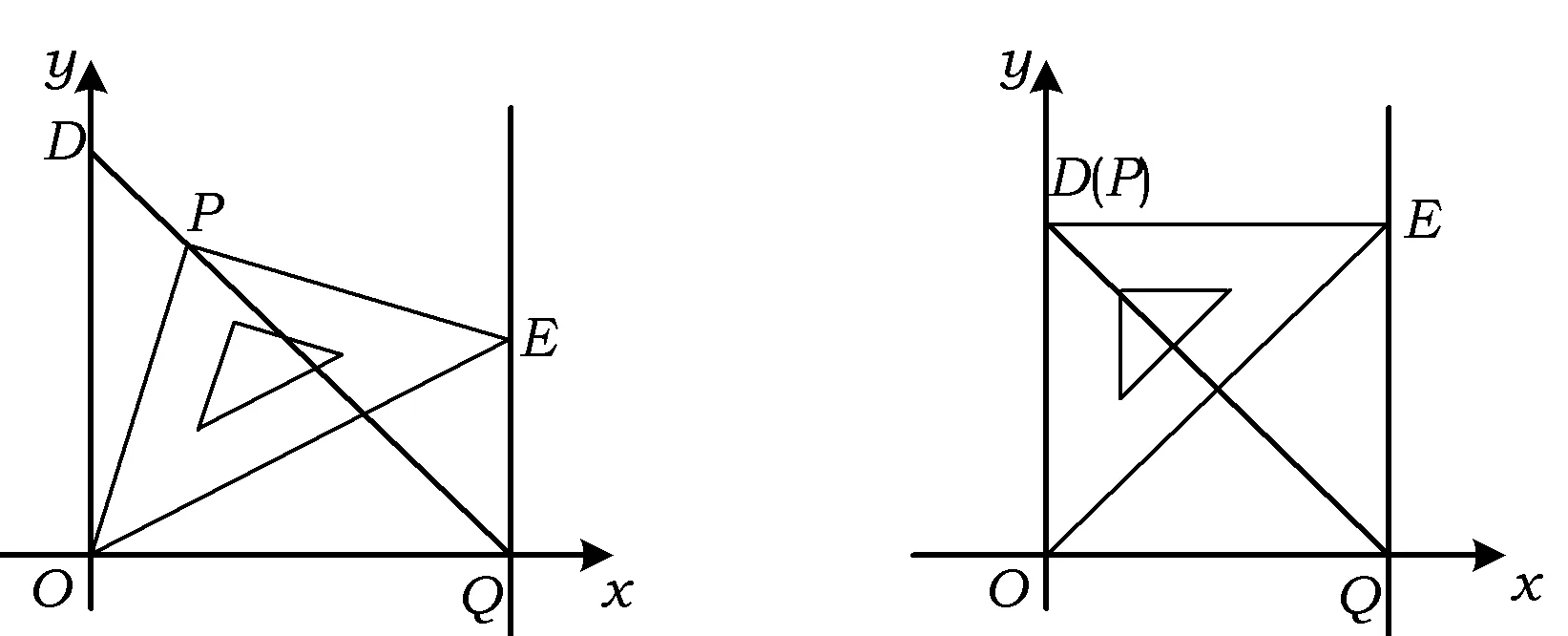
图8 图9

各小组经探究归纳得出结论:如OD=OQ;△ODQ是等腰直角三角形；DQ平分∠OQE；DQ与x轴的夹角为45°;△DOQ与△OPE相似；……

在思维受阻时，铺设台阶，引导学生将图形特殊化，如将三角形的一边固定在y轴上(如图9)，或者将边OE固定在x轴上，得出结论后，再旋转三角板进行操作验证，这实际上给出了引导学生探究问题的一种方法——特殊与一般的转化.

教师继续呈现如下问题串，随后组织小组汇报研究成果,教学片断如下:

问题6从得出的结论看，其本质是“DQ与x轴的夹角45°”，根据图形特征你可以联想到什么数学知识？

生1：由“DP是∠OQE的角平分线”联想到角平分线定理.

师：既然联想到角平分线定理，能否把图画出来，说说你的发现？

学生动手画图，1分钟后回答问题.

生2：过点P作∠OQE两边的垂线(如图10)，这样就构造了△PMO≌△PNE，从而PM=PN,可得∠PQO=45°.

师：刚才构造全等三角形时充分利用了等腰△OPE的性质，还有其他构造方法吗？

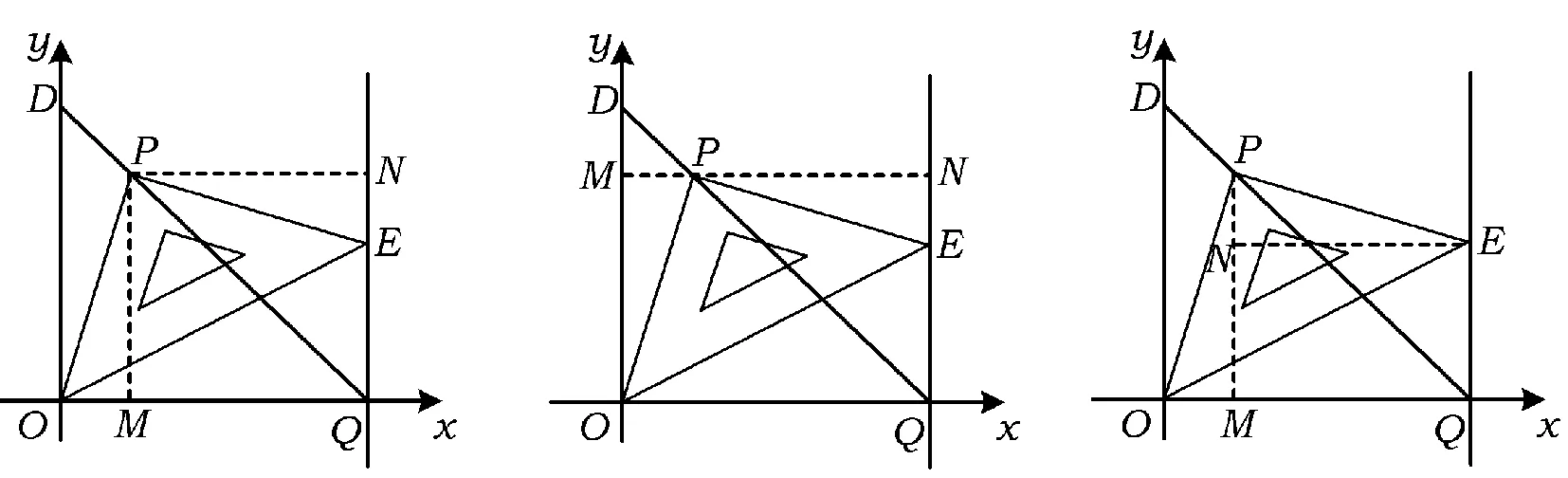
图10 图11 图12

生3：过点P作x轴的平行线，构造△PMO≌△PNE,得PN=QN,从而∠PQO=45°(如图11).

生4：也可以过点P作PM⊥x轴，过点E作EN⊥PM，构造△PMO≌△PNE来说明PM=MQ,有∠PQO=45°(如图12).

生5:过点O作OM⊥DQ，过点E作EN⊥DQ(如图13)，可以构造△OPM≌△PNE,只要说明OM=QM或者EN=QN就可以得到∠PQO=45°.

师：刚才这2种构造的方法，可以看成是由“∠PQE=45°或∠PQO=45°”联想此角为等腰直角三角形一内角,如图12，作PM⊥x轴，即可构造等腰Rt△PMQ，我们还可以如何构造等腰直角三角形？

生6：过点P作PM⊥DQ(如图14)，可以构造△MOP≌△PEQ.

生7：由∠1+∠3=∠2+∠3=90°，得∠1=∠2，又∠MOP+∠POQ=∠PEQ+∠POQ=180°,则∠MOP=∠PEQ，而OP=PE,因此△MOP≌△PEQ,从而PM=PQ,即△PMQ为等腰直角三角形，得∠PQM=∠PMQ=45°.

图13 图14 图15

生8:我发现过点P作PN⊥DQ(如图15),也可以构造△NPQ≌△OPQ.

师：很好，刚才都是从其中一个45°角来寻求解题思路，另外从图形特点角度考虑还能联系什么知识？

生9：由“四边形OPEQ有2个直角”可以联想到补全直角三角形.

师：好，大家试试，并说说你的发现.

学生思考，动手在图上画，寻求思路.

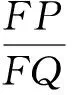
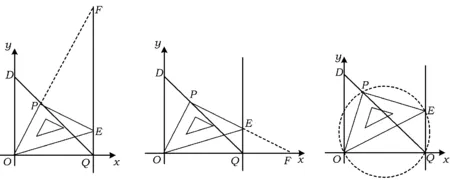
图16 图17 图18

生11：延长OP交x轴于点F,也可以补全Rt△OPF(如图17)，同样可求解.

师：刚才有同学注意到“四边形OPEQ有2个直角”，这个图形还可以看成什么，可以联想到什么数学知识？

生12：2个直角三角形Rt△OPE与Rt△OQE有共同斜边OE.

生13：以OE为直径作圆.由∠OPE=∠OQE=90°,可知点P,Q都在该圆上，这样有圆周角∠PEO=∠OQP,从而得结论∠PQO=45°(如图18).

在这一教学过程中，教师通过问题引导，铺设思维台阶，从图形特征、符号信息中联想其他知识，为添加辅助线提供思考角度，不仅让学生自己解决了问题，降低了例题难度，更重要的是加强了知识间的联系，增强了学生探究问题的兴趣和思维的发散.

(2)反思解题思路，暴露思维.

在让各充分小组说出解题思路后，教师引导学生反思解题时的思考，在反思中小结.前6种方法(图10～图15)都是由一个45°角联系到等腰直角三角形的一个内角构造全等三角形，但构造时思考的角度是不一样的，添加辅助线，实现了转化；图16、图17的方法是基于四边形OPEQ有2个直角的图形特点，延长线段补全直角三角形，转化为三角形相似问题;图18的方法是基于2个直角三角形有公共斜边，与圆的知识相联系，补全圆后，就转化为圆周角问题；图10、图14与图15的方法，也可以从图形的旋转角度去总结.

在解题时，学生往往只关注自己解题时的探究，不理会他人的思考，通过对所有解题分析的反思，分享同伴的解题思路，继续暴露数学解题的思维.这不是简单的一题多解，而是从数学思想方法上进行归纳、提炼，使数学解题与智力发展同行.

(3)构造基本图形，学以致用.

完成例题，要求选用上课没想到的方法.

(4)适当变式练习，拓展提高.

作业若直角边之比为2∶3的直角三角形的一个顶点与点C重合，直角顶点D在直线BQ(点D不与点Q重合)上，另一个顶点E在PQ上，试求点P的坐标．

3 教学思考

3.1 铺设台阶，有效突破学习难点

学习难点的突破，需要创设优化的学习环境，用“问题情境”帮助学生进行数学“意义建构”，2种设计都是在分析例题背景后提炼出几何模型，帮助学生理解例题所反映的本质.由于三角板是学生熟悉的，起到了“脚手架”的作用，使学生的探究活动得以有效展开，解题时顺利添加辅助线，突破难点.

但是，同样的内容教学，不同的问题创设，达到的教学效果不同.教学设计1解题看似顺畅，其实是定性思维，表现为解题思路单一，影响学生思维的展开.教学设计2先让学生尝试解决，思考5分钟无明显思路,开始呈现问题串，问题串的引领将多个知识点包含在一起，让学生变换观察图形的视角，把自己的注意力集中在问题的引导上，根据图形特点从不同角度、不同知识产生联想，使学生的思维可视化，促使学生多角度参与，来提升思考深度,产生不同的解题思路，达到“一题多解”的效果.教师在学生的困难处、受挫时进行引导，受挫后的成功体验更能激发学生继续探究的的欲望,激发学习动机.

3.2 问题驱动，加强知识之间联系

解题教学的目的是以典型例题为载体，通过例题的解答，为学生搭建知识框架，建立知识之间的联系，使知识系统化，促进学生的认知发展.如何在知识之间建立起合理的、实质的联系？这就需要问题驱动.2种设计都关注了创设问题情境，来帮助学生对知识的迁移，教学设计1通过问题及其2个变式的引导，从一个基本图形联系相似或全等知识.教学设计2围绕着问题串的思考，从45°角联想到等腰直角三角形，从一个四边形2个内角为直角联想到直角三角形和圆，从等腰直角三角形联想到图形的旋转，并灵活应用相关知识，添加辅助线.设置这类蕴含研究思考过程的问题，学生从中学会联系、学会转化，达到铺设思维台阶的目的.

3.3 关注过程，内化数学思想方法

掌握数学方法和数学思想，形成解题策略及思维品质，是数学教学的目标.这就要求例题教学不能就题论题，而是要把分析探究过程作为一种方法来引导.在依据几何图形来解决问题的同时，要设计合理的问题，引导观察，鼓励直觉判断，让学生参与分析题意、寻求解题思路的过程，体现过程意识.如在教学设计2中，引导学生通过三角板位置的特殊化，来探究结论，根据图5的图形特点，以问题串的形式，从不同角度产生对数学知识的联想，逐步引导学生思考，有效提炼基本图形，为寻求解题思路提供了可能，归纳出解题的一般方法与特殊方法，让学生在不同的情境下有多种机会去应用他们所学的知识(将知识“外化”)，经历数学活动过程，使思维层次不断提高，从中体会、感悟所蕴涵的思想方法,积累解题经验.

[1] 罗增儒.怎么样学会解题[J].中学数学教学参考:初中版，2009(3):7-9.

[2] 顾继玲.让学生经历“数学化”的过程[J].中学数学教学参考:初中版，2011(7):2-4.

[3] 罗增儒.分析解题过程的操作[J].中学数学教学参考:初中版，2009(5):9-14.

[4] 乌美娜.教学设计[M].北京：高等教育出版社,1994.