坚持标准 关注本质 引领教学——2012年浙江省台州市学业水平考试命题的实践与思考

●

(仙居县教研室 浙江仙居 317300)

坚持标准关注本质引领教学
——2012年浙江省台州市学业水平考试命题的实践与思考

●吴增生

(仙居县教研室 浙江仙居 317300)

初中毕业生数学学业水平考试是一种标准参照考试，其功能是评价学生初中阶段数学学习达成课程标准要求的水平，这类考试还承担了高中招生选拔的功能.正是这种功能，引起了学校的高度重视，同时出现了“压缩新课教学进程、长时间复习、大运动量训练”等不良教学现象，给学生造成了过重的学习负担.在坚持标准参照考试性质，适当体现学习潜能评价，科学合理评价学生的学业水平的基础上，充分发挥区域性考试的教学导向功能，虽然对扭转不良教学现象不能起釜底抽薪的作用，但还是有一定的作用.基于此，2012年台州市学业水平考试试题，在继承前几年特色的基础上，作出了适当的调整与创新.

1 坚持标准

坚持标准要求命题以课程标准和考试说明为依据，这是保证标准参照考试性质的前提，也是科学合理地评价学生学业水平的基础.

整卷布局按照容易题、稍难题和较难题的权重(分值)7∶2∶1进行，关注在核心知识的中间地带命制试题，重点考核心知识和思想方法，穿插考一般知识.

如对函数的考查，第7题考查反比例函数的增减性；第19题考查反比例函数和正比例函数的解析式和图像；第23题考查二次函数的图像及性质；第24题又考查了用函数表示几何度量的变化规律.既覆盖了初中3类基本函数，又重点考查了函数模型思想；既以函数增减性这一核心知识为考查重点，又兼顾了函数解析式、函数图像等相关知识.其中第7题为容易题，第19题为稍难题，第23题和第24题为较难题.

再如，几何的核心知识是三角形、平行四边形和圆的基本性质、图形的全等变换(包括平移、轴对称和旋转)及相似三角形的性质和判定，对这些核心知识的考查体现在第2～4,6,10,14～15,22,24题中.其中第2～4,6,14题为容易题，第15题和第22题为稍难题；第10题考查菱形的轴对称性、锐角三角形函数，要求运用图形变换思想解决问题，属于较难题；第24题是新的几何对象及其性质的探究，涉及到的知识点有：平移、平行线、勾股定理、相似三角形、矩形、圆、函数、方程、不等式等，涉及到的数学思想方法有：分类讨论思想、数形结合思想、方程思想、数学类比等，是新背景下的数学对象的探究，属于较难题.

对于统计和概率领域的考查，以统计分析和决策为考查重点.如第8题考查统计量意义的理解，而不考查统计量的计算；第21题考查在现实背景下的数据分析和决策过程.

考虑到学习困难学生的实际情况，容易题比往年更简单.如第1～7,11～13题都只考查一个知识点，共计43分.第17题和第18题都是简单的代数计算和解一元一次不等式组问题，共计16分.这样，最简单的题就有近60分，而且在综合题中，也有容易得分的小题，整卷的基础性体现得比较充分.

2 关注本质

关注本质，就是要关注数学最显著的学科特点——抽象性、逻辑严谨性和应用广泛性；重视数学抽象概括、模型和推理计算这3个基本思想；重视数学应用；关注初中数学常用的数学思想方法如分类讨论、数形结合、函数方程、数学模型、图形变化、数学转化、特殊化与一般化的考查；重视诸如数学感知、数学表征、数学抽象概括、数学推理计算等认知水平的考查；重视知识的理解、思想方法的感悟；重视数学大智慧，而不是追求解题小技巧.

如第24题创设了数学概念学习和几何探究的新背景，以距离这一几何核心概念为出发点，引进了两线段之间距离这一新概念，这一概念与两点之间的距离、点到直线之间的距离、2条平行直线之间的距离等概念相联系，要求学生理解这一新概念并用这一概念表示和研究图形的性质.在这个问题的解决中，包含了对概念理解、解释、运用的考查.在理解这一概念过程中，需要比较初中阶段学习过的几种距离概念，理解平移的概念，需要用新概念描述线段的平移，想象“两线段之间距离为2”的几何模型,需要用函数观点、数形结合、方程的思想分析和解决问题.总之，该题对数学感知、数学表征、数学抽象概括、数学推理计算等数学认知水平进行了全面的考查.第24题原题如下：

定义：P，Q分别是2条线段a和b上任意一点，线段PQ长度的最小值叫做线段a与线段b的距离．已知O(0，0)，A(4，0)，B(m，n)，C(m+4，n)是平面直角坐标系中4个点．

(1)根据上述定义，当m=2，n=2时(如图1)，线段BC与线段OA的距离是______；当m=5，n=2时(如图2)，线段BC与线段OA的距离(即线段AB长)为______．

(2)如图3，若点B落在圆心为A，半径为2的圆上，线段BC与线段OA的距离记为d，求d关于m的函数解析式．

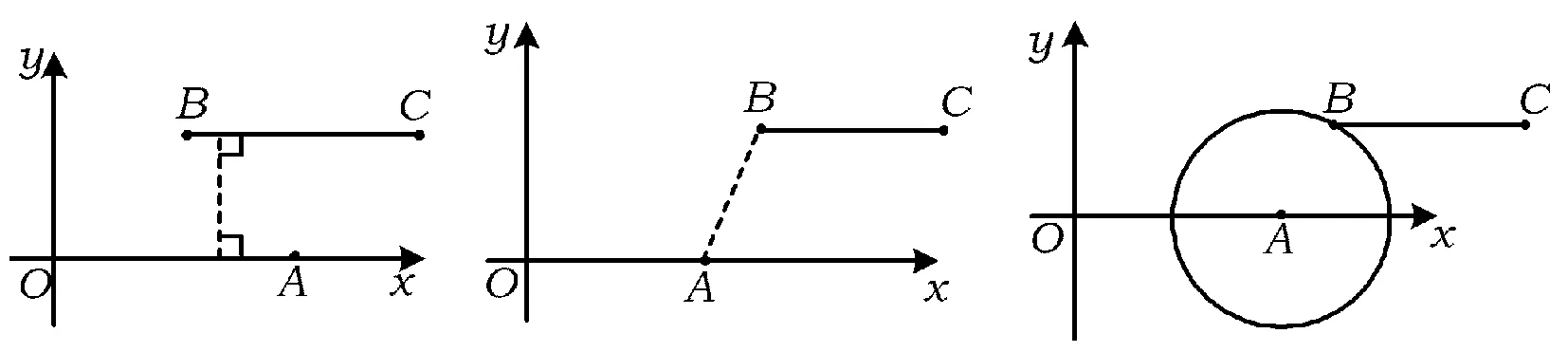
图1 图2 图3

(3)当m的值变化时，动线段BC与线段OA的距离始终为2，线段BC的中点为M．

①求出点M随线段BC运动所围成的封闭图形的周长.

②点D的坐标为(0，2)，m≥0，n≥0．作MH⊥x轴，垂足为H.问是否存在m,使以A，M，H为顶点的三角形与△AOD相似?若存在，求出m的值;若不存在，请说明理由(备用图如图4和图5所示)．

图4 图5

再如，第16题：

请你规定一种适合任意非零实数a，b的新运算“a⊕b”，使得下列算式成立：

1⊕2=2⊕1=3；

…

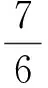
你规定的新运算a⊕b=________(用含a，b的一个代数式表示).

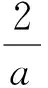
第23题改编于人教版教材中的习题：

某汽车在刹车后行驶的距离s(单位：米)与时间t(单位：秒)之间关系的部分数据如表1所示：

表1 刹车后行驶的距离与时间之间的关系

假设这种变化规律一直延续到汽车停止．

(1)根据这些数据在图6的坐标系中画出相应的点.

图6

(2)选择适当的函数表示s与t之间的关系，求出相应的函数解析式.

(3)①刹车后汽车行驶了多长距离才停止？

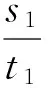
在近几年的考试中，有2类函数题型出现的频率非常高：一类是以图像为背景的有解析几何倾向的问题；另一类是用函数研究图形变化下的某些度量属性的变化规律.其实，函数最明显的特征是模型属性而非图形属性，画函数图像是为研究函数的性质服务的，而不是为了研究图像而研究图像.虽然初中的函数具有数形结合的特点，与高中解析几何有着密切的联系，但作为学业水平考试，应该重点关注其本质特征.第23题就是回归函数的本质属性，关注函数的模型属性，考查了学生根据部分对应关系合理选择函数类型进行模拟并求出函数解析式，研究函数的最值，体现了函数思想中“考查回归本质、重视知识应用”的命题思想.

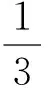
3 引领教学

作为与学生升学有关的大型区域性考试，导向教学是学业水平考试的重要功能.在当前教学实践中，普遍存在着重教轻学、重训练轻理解、重知识轻思想、重结果轻过程、重技巧轻智慧的现象.这些教学中的不良价值取向的核心原因是应试教育思想在作祟.教师不重视在课堂教学中让学生通过独立思考和相互交流理解知识、体会数学思想.概念教学“一个定义、三点注意”，拼命把知识塞给学生，再通过大量练习进行巩固.新课教学囫囵吞枣赶进度，留出大量的时间搞训练型复习.在复习教学中，没有让学生通过自己的思考理解知识之间的相互联系，建立知识网络，而是以过度训练来达成解题熟练和提高解题速度.不是认真研究课程标准、考试说明和教材，而是热衷于做大量中考陈题，热衷于猜题压题.作为学业水平考试的命题者，担负着引领教师、摒弃这些教学弊端、改进教学的责任.

怎样才能使学业考试担负起这一使命呢？

首先，应该全面贯彻课程标准和考试说明，把握试卷的整体难度，本卷总体难度为0.70左右,符合考试说明的要求.

其次,要重视对数学知识的理解和数学思想方法的感悟,重视大智慧,摒弃小技巧.如第16题着重考查数学概括,而很少涉及具体的知识;第10题着重考查对称思想;第24题重点考查对数学新概念的理解和应用,考查学生用所学概念进行解题的能力，研究新概念对象的几何性质.