挖掘数学思想 探究数学本质——2012年浙江省数学高考函数问题评析

●

(昌硕高级中学 浙江安吉 313300)

挖掘数学思想探究数学本质
——2012年浙江省数学高考函数问题评析

●黄超

(昌硕高级中学 浙江安吉 313300)

函数问题，历来是高考的重点和难点，也往往是试卷的亮点：初看平淡无奇，细看则韵味悠长；乍看举步维艰，细想则豁然开朗．浙江卷中的函数试题具有其鲜明的特色，许多问题成为教师津津乐道的经典和师生共同探究的范例，值得细细体会.以下通过对2012年理科第17题的详细评注和近年来的经典函数试题的简要分析，与大家一起体验浙江卷函数问题的特色以及高考复习的方向．

例1设a∈R，若x>0时均有

[(a-1)x-1](x2-ax-1)≥0，

则a=______.

(2012年浙江省数学高考理科试题)

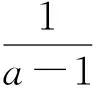
图1 图2

注问题的呈现形式为已分解为一次和二次因式乘积的三次多项式不等式求解集，故可以自然联想到利用三次多项式函数的图像解题，这是函数思想的直接体现.其以三次多项式函数图像的整体认知为基础，经过定性和定量的合理转化，借助图像的直观性可以较顺利地发现“等根”这个解题核心，对函数零点的理解是画图的关键.可能造成解题歧路的是部分学生的思维定势，即三次多项式函数问题用求导转化为最值问题来解决，但参数讨论的复杂性导致此法行不通.命题者没有将问题表述为

(a-1)x3-(a2-a+1)x2+x+1≥0，

既在一定程度上指出了问题的思考方向，也在难度上做了较好的控制.这与浙江卷“多考一点想、少考一点算”、“多考通法、少考特殊技巧”等命题理念是紧密相关的，也正是浙江卷的一个鲜明特点.

解法2令f(x)=(a-1)x-1，g(x)=x2-ax-1，f(0)=g(0)=-1,故y=g(x)有正零点.由题意，f(x),g(x)有相同的正零点，如图3所示，则

因此

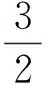
注既然问题已分解为一次和二次因式的乘积，则根据2个函数值正负变化的同步性，将不等式问题转化为一次函数和二次函数的零点问题，化一般为特殊，以函数图像作为破解问题难点的切入口，函数、方程、不等式相互转化，清晰简洁完满，体现了数形结合的思想.解题的核心在于以形助数，借助2个函数值的正负变化化简问题，分合之间彰显图像的解题魅力.

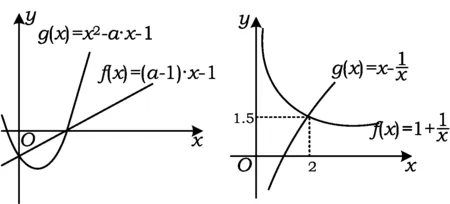
图3 图4

解法3由x>0，原不等式可化为

若存在x0>0使得

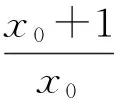
则

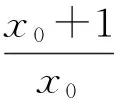
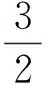
解法4由x>0，原不等式可化为

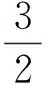
解法5由x>0，原不等式可化为

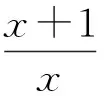
注经过参变分离，将问题转化为求解关于a的不等式的解集问题，在解法中运用了不等式的“两边夹”原理.解法3借助特殊化的思想将问题简化为方程根的问题；解法4将之转化为恒成立问题并借助求函数值域的方法；解法5利用函数图像较为简洁地说明了问题.从某种意义上说，解法4和解法5也可看作是对解法3的一种解释.这种包含参变分离的转化思想也正是解决函数问题的重要方法之一，巧妙的方法背后往往有较为深刻的背景.

解法6当x=2时,

(2a-3)(3-2a)=-(2a-3)2≥0，

因此

注集简、巧、灵于一身，如有神助，堪称绝妙.为什么是x=2？从以上的解法中可以看出这不是巧合，但作为解题，这里显然有极大的运气成分.如果解题有障碍，作为应试策略，尝试代入一些特殊的值不失为一种好的解题方法，这也符合特殊和一般的辨证关系.当然，这样的妙解多用于欣赏，有时甚至有“事后诸葛亮”之嫌，故不宜大加渲染，度的把握值得注意.

从以上对试题的解答和注看，此题较为清晰地展现了浙江卷中函数问题的鲜明特色，即思想的深刻性、思维的简洁性、方法的多样性、图像的直观性、函数的二次性，其着眼点在于对数学思想的深刻考查和对数学能力的理性诉求.

1 想一想，思想深刻思路简

数学思想方法是数学的本质之所在，是数学的精髓.数学思想和方法是数学知识在更高层次上的抽象和概括，它蕴涵在数学知识发生、发展和应用的过程中.高考试题坚持能力立意，对数学思想方法的考查往往是深刻而内蕴的，但在深刻理解的基础上解题，思路却是简洁的.

例2已知a是给定的实常数，设函数f(x)=(x-a)2(x+b)ex，b∈R，x=a是f(x)的一个极大值点,求b的取值范围．

(2010年浙江省数学高考理科试题)

图5

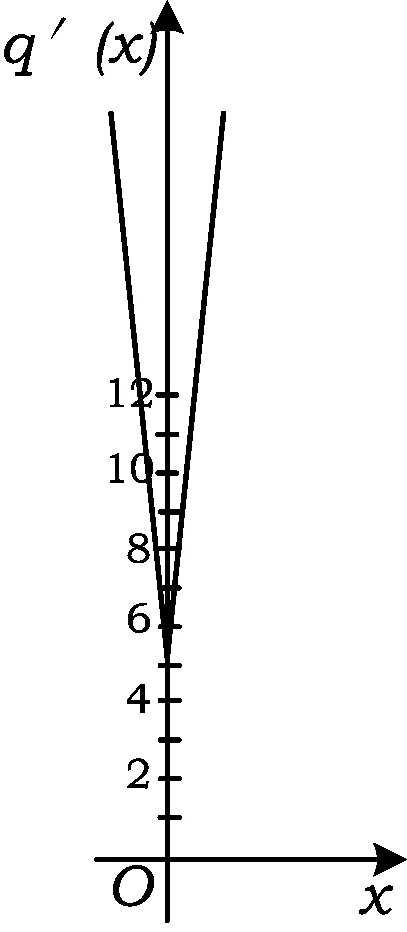
注根据极大值的含义，由题设中“x=a是f(x)的一个极大值点”，可知在x=a的某个邻域内的任意一个x的值，均有f(x)

“数学味”源自何处？到底是什么能令人击节赞赏，顿觉眼前一亮？以蕴涵于试题背后的学科本质及数学思想的高立意为支撑设计的试题就有这样的神奇.

2 看一看，图像直观本质显

华罗庚先生曾言：“数缺形时少直观，形少数时难入微，数形结合百般好，隔裂分家万事休.”利用图像的直观性解题是重要的思考方法之一，体现了数形结合的数学思想.函数图像不止是直观地反映了函数的性质，而且能充分简化思维的过程，体现问题的本质.如例2的解决就充分利用了图像的直观性.

例3已知函数f(x)=x3-(k2-k+1)x2+5x-2，g(x)=k2x2+kx+1，其中x∈R.

(1)略；

(2009年浙江省数学高考理科试题)

注当x<0时,

q′(x)=f′(x)=

3x2-2(k2-k+1)x+5；

当x>0时,

q′(x)=g′(x)=2k2x+k.

图6

因为当k=0时不合题意，因此k≠0，q′(x)的图像左侧为二次函数一部分，右侧为一次函数一部分.由题意，结合图像(图6)可知k=5满足题意．图像的直观性使问题显得自然和谐，解答思路简洁明快，充分体现了数形结合的魅力.

再如，2012年理科第9题将函数图像与不等式问题进行了巧妙的结合，通过画图答案一目了然.这样的试题在历年的浙江卷中比比皆是，理由很简单：此类试题既能深层次地考查函数的性质，又能充分考查数形结合思想.

3 选一选，方法多样数感联

高考试题具有丰富的内涵，因此其解决的方法也具有多样性，从不同的角度切入，就会有不同的发现，而这些方法的背后耸立着数学思想的丰碑.如何选择合适的方法，和学生平时对各种方法的熟悉程度有关，在一定意义上考查了学生对数学解题的感觉.

例4设x,y为实数，若4x2+y2+xy=1,则2x+y的最大值是______.

(2011年浙江省数学高考理科试题)

注此题解法众多，也引发了一些较为深入的研究.笔者简单罗列了一下，至少可以写出13种解法，比如判别式法、不等式、参数方程、换元法、向量法、函数法等等.各种方法是有繁简之别的，但其背后都有着数学思想的支撑.这其实也是我们平常教学的好素材.

4 导一导，二次函数威风见

导数是解决函数单调性问题的重要工具，而二次函数的考查是数学高考的永恒主题，“3个二次”的问题值得细细研究，牢牢掌握.

例5已知函数f(x)=x3-(k2-k+1)x2+5x-2，g(x)=k2x2+kx+1，其中k∈R.设函数p(x)=f(x)+g(x),若p(x)在区间(0,3)上不单调，求k的取值范围.

(2009年浙江省数学高考理科试题)

注将“p(x)在区间(0,3)上不单调”转化为“p′(x)=0在(0,3)上有实数解，且无重根”，问题即转化为二次函数问题(或二次方程根的存在问题，即“3个二次”的问题).结合图像，或直接根据二次函数的图像分类，或利用参变分离加以转化，都可以解决此题.

例6已知a>0,b∈R，函数f(x)=4ax3-2bx-a+b.

(1)证明：当0≤x≤1时，①函数f(x)的最大值为|2a-b|+a；②f(x)+|2a-b|+a≥0.

(2)若-1≤f(x)≤1对x∈[0,1]恒成立，求a+b的取值范围.

注第(1)小题第①问利用导数求函数的单调性，并利用二次函数的性质(开口向上的二次函数在闭区间上的最大值只能是端点值)得到

f(x)max= max{f(0),f(1)}=

max{-a+b,3a-b}，

然后利用要证明的结论明确分类标准并合并.此题看上去并不难，但不熟悉二次函数最值性质的学生可能会将这个问题复杂化，即增加分类.第(1)小题第②问将2类情况中f(x)+|2a-b|+a统一缩小为2a(2x3-2x+1)并进而通过求导转化为二次函数问题.此问也可不化归为统一函数而直接用分类讨论解决，但过程繁冗.此题的特点:思考的力量远高于具体的运算，其涉及函数与方程、分类与整合、数形结合、化归与转化等基本数学思想．

再如，2012年数学高考理科第16题通过新定义问题，利用导数求切线或利用配方法求二次函数的最值，以解析几何为载体考查函数问题；理科第21题利用二次函数性质求最值的问题等等．

通过以上分析可以看到：浙江卷中的函数问题是高考的重点和难点，是命题者精心设计试题的着眼点．其注重对数学思想的深入考查;注重数学本质的理性挖掘；注重图像的演绎，通过图像可以快捷地解决那些难度较大的把关题；注重二次函数的考查，“3个二次”在函数问题中比比皆是．因此，在高三复习教学中，依靠“题型+技巧+大运动量训练”的教学难以适应高考，只有突出数学本质、实现高中数学教学的自然回归才是复习的方向.具体而言：

(1)作为函数复习，应更多地关注函数本身的性质，关注函数图像.遇到函数问题，多让学生尝试画图，用图像来思考和解决问题，当然，这其中有一些工具不可或缺，如导数等．

(2)关于导数，必须明确的是导数只是研究函数单调性和极值的工具，过多地关注导数处理问题的技巧是本末倒置．

(3)“3个二次”的问题是浙江卷考试的重点也是难点，在复习中要引起充分重视，要不断挖掘其中的变化，让学生通过诸多的变式深刻体会二次函数的本质以及衍生出的种种问题.

(4)数学思想是数学学习的灵魂，对其的渗透非一朝一夕之功，需要教师通过各种问题有意识地加以培养，变隐形的思想为显性的方法，变抽象的理念为具体的策略，以期让学生能自觉地加以运用．