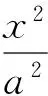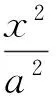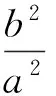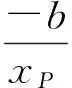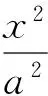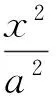讲清数学道理 揭示数学本质
——提高高三数学复习效率的教学策略
●
(萧山中学 浙江萧山 311201)
讲清数学道理揭示数学本质
——提高高三数学复习效率的教学策略
●李金兴
(萧山中学 浙江萧山 311201)
高三学生学得辛苦,但由于缺乏对数学问题本质的认识,常常事倍功半,在重复与茫然的训练中效率不高.因此,教师的指导作用应该体现在“讲清数学道理,揭示数学本质”上.通过教师自身或集体研究,帮助学生反思学习过程、领悟数学背景,从数学知识的根源开始,沿着习题变式的途径理清每一类问题的来龙去脉,使得数学知识“拎起来成一串、撒下去铺一片”,这样才能让学生举一反三,实现教学轻负高质的目的.
本文就高三复习阶段如何讲道理、揭本质例举几个典型问题,以期抛砖引玉.
1 新授课讲不清的道理,到复习课来讲
用斜二测画法画几何体的直观图,操作步骤十分简单:画轴后,使平行于x轴或z轴的线段长不变,平行于y轴的线段长减半.但按上述方法画的直观图是几何体的“平行投影”吗?如果是,投影面和投影线方向如何确定呢?如何描述投影线方向?
文献[1]对此作了阐述,得到结果:此时投影线与投影面成arctan2角.但这一结果并不能完全确定投影线的方向,可进一步作如下探究:
将水平放置的长方体ABCD-A′B′C′D′的直观图(如图1)看作一个平面图形(投影),考虑到平面四边形ABB′A′、平面四边形DCC′D′与原图形全等,因此投影面与长方体侧面ABB′A′平行.特别地,不妨以长方体侧面DCC′D′所在平面为投影面.
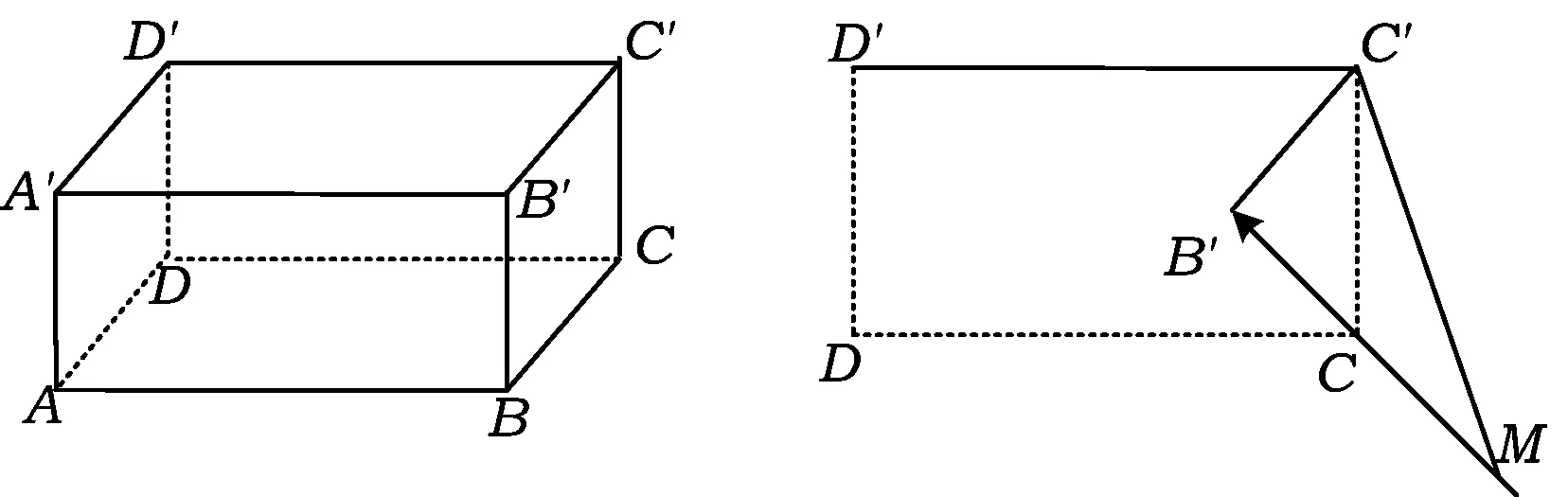
图1 图2
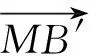

图3
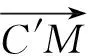
设M(2,0,0),则
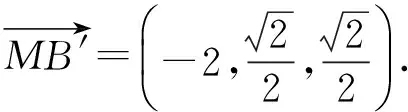
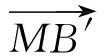

从而投影线与投影面成arctan2角(文献[1]的结论).同理,设j=(0,1,0),k=(0,0,1),可求得
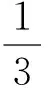
反思斜二测画法新授课学习时还没有引入空间向量,因此可以在高三复习课阶段补充该知识.
2 学生一错再错的道理,将错就错地讲
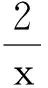
2.1 从反例来辨别
先仿照此类错误解法,举例“对于函数y=x2+1(x>0),因为当x>0时,x2+1≥2x,当且仅当x=1时等号成立,所以当x=1时,ymin=2”,这个结论显然是错误的(明确指出这种解法是错误的).
2.2 分析反例错因
让学生在同一坐标系中比较y=x2+1和y=2x的图像,便知“x2+1≥2x”只说明y=x2+1的图像始终在y=2x图像的上方,“当且仅当x=1时等号成立”只说明2个图像相切于点x=1处,切点并非图像的最低点(如图4),y=2也并非函数y=x2+1(x>0)的最小值.
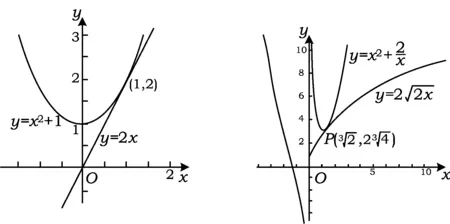
图4 图5
2.3 反思错解成因
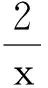
3 解题方法巧妙的道理,辩证透彻地讲
数学题经常能一题多解,除了常规解法,教师应对“巧思妙解”作辩证分析:有些巧解很难想到,实用性不强;有些巧解变换情景后可能成为错解,应谨慎采用.
3.1 这样的巧解对不对
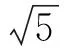
(2008年浙江省数学高考试题)
巧解(错解) 两边求导,得
-sinα+2cosα=0,
从而
tanα=2.
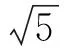
3.2 为何有这样的“巧思妙解”
例2已知函数f(x)=lnx+ax2+bx(a≤0).
(1)若2a+b+1=0,讨论函数的单调性;
参考答案简述如下:
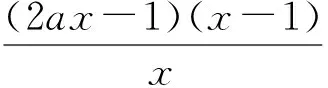
(2)证明取a=-1,b=1,则
f(x)=lnx-x2+x.
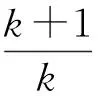
当k取遍1,2,3,…,n并相加,即得
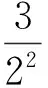
分析对于第(2)小题的答案,学生普遍感到取a=-1,b=1来构造函数f(x)=lnx-x2+x,非常巧妙但很难想到.事实上,若尝试用数学归纳法证明第(2)小题,则由假设n=k时结论成立推证n=k+1时结论也成立的过程中,只要证明不等式

即
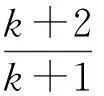

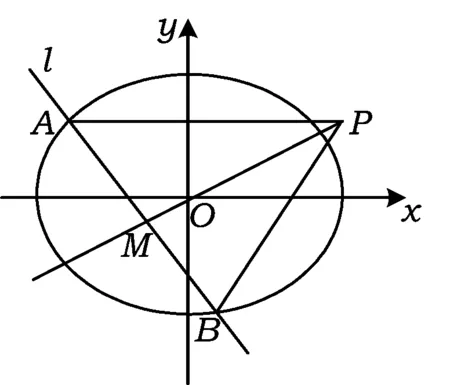
因此只要证当x>1时,lnx 反思对于一些难度较大的问题,若答案过于“巧妙”,则学生容易对这类问题产生“敬畏”之心,不利于数学学习兴趣的培养.教师应该让“巧解”自然呈现其真面目,让学生有信心去创造“巧妙”解法. “细节决定成败”很多时候能解释学生“会而不全”的道理,教师讲授时要将这些细节放大后细致地讲. 图6 (1)求椭圆C的方程; (2)求△ABP面积取最大值时直线l的方程. (2012年浙江省数学高考理科试题) (2)设AB的中点为M(2t,t),由点差法易得直线AB方程为 代入椭圆方程,整理得 3x2-12tx+16t2-3=0, 设f(t)=(3-4t2)(1-t)2,则 f(t)=-4t4+8t3-t2-6t+3, 从而 f′(t)=-16t3+24t2-2t-6. 至此,不少学生因为不能对f′(t)的表达式进一步因式分解,导致解题不全.事实上,由f(t)=(3-4t2)(1-t2)得 f′(t)= -8t(1-t)2-2(3-4t2)(1-t)= -2(t-1)(8t2-4t-3), 反思将f(t)=(3-4t2)(1-t)2的表达式先展开再求导这一细节是导致解题失败的关键因素,教师也可在复习导数应用时专门对此进行针对性复习. 又如2011年全国高中数学联赛(一试)第7题: 例4直线x-2y-1=0与抛物线y2=4x交于点A,B,点C为抛物线上的一点,∠ACB=90°,则点C的坐标为______. 分析联立方程,消去x得 y2-8y-4=0, 因此以AB为直径的圆,其圆心为(9,4),半径为 联立 即可求得点C坐标.该方程组消去x,整理得 y4-56y2-128y-48=0. 至此,不少学生因为不会解四次方程而无法完成解题.事实上,因为点A,B的坐标也是方程组的解,所以上述四次方程必有因式y2-8y-4,从而由 y4-56y2-128y-48= (y2-8y-4)(y2+8y+12)=0, 解得点C的坐标为(1,-2)或(9,-6). 反思不能利用“A,B的坐标都是方程组的解”这一细节是导致解题失败的关键因素,类似问题在高考题中也有出现,教师应将这种细节放大,培养学生阅读题意、挖掘隐含条件的意识. 从而 即点M与短轴顶点B1,B2的连线的斜率之积为定值.设MB1,MB2与长轴分别交于点P,Q,则 因此 xP·xQ=a2, 而这恰恰就是|OP|·|OQ|=a2的数学本质. 即 从而同样有定值|OP|·|OQ|=b2. 利用坐标和线段长的对应关系这一数学本质,同样可研究抛物线相关问题.例如,抛物线y2=2px(p>0),点A,B,C在抛物线上,BC⊥x轴,AC,AB与x轴交于点D,E,则xD+xE=0,即|OD|=|OE|. 反思典型例题之所以典型在于它反映了数学知识间的一种本质联系,使解题者能通过一道习题的研究掌握一类问题的解法,使教师能以此为例清晰地剖析出数学知识间的本质联系,不仅在内容上还能在方法上有利于进一步探究新知. 高中数学和数学教学的道理远不止本文例举的几类.通过教学,教师向学生展示各种数学概念、公式、法则、性质、结论,其目的是让学生对数学“知其然”;引导学生对数学结论进行推理论证、应用推广是让学生对数学“知其所以然”;而向学生讲清数学道理、揭示数学本质是让学生对数学“知其所以所以然”. “数学要讲推理,更要讲道理”,如果在教学中只讲推理不讲道理,那么教师教给学生的仅仅是数学解题的方法和技术,缺乏数学思想的渗透,从而难以提高教学质量. [1] 沈建刚.斜二测画法的一次“寻根”之旅[J].中学数学教学参考,2010(1/2):26.4 学生会而不全的道理,放大细致地讲
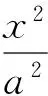
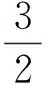
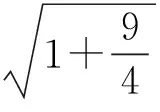
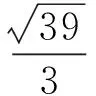
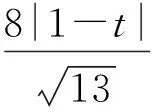
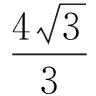
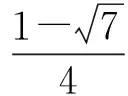
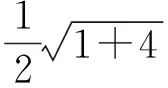
5 类比探究的道理,深入本质地讲