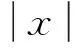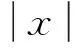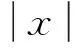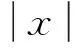一个不定方程及其他的整数解

2013-10-24 00:49周梅

重庆工商大学学报（自然科学版） 2013年9期

关键词：解性奇数偶数

周梅

(重庆师范大学数学学院，重庆 401331)

一个不定方程及其他的整数解

周梅

(重庆师范大学数学学院，重庆 401331)

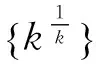
不定方程；初等方法；整数解

不定方程的研究历来受到人们的重视，大部分的不定方程看似简单，求解起来却是相当的困难.方程的未知数增多，从而难度增大，解的个数也增加.刘燕妮、郭晓燕[1]研究了不定方程xy+yz+zx=0的可解性，得到了它的全部整数解；霍梦圆[2]研究了不定方程xy+yz+zw+wx=0的可解性，得到了它的若干整数解.此处将xy+yz+zw+wr+rx=0的研究结果整理了出来.

1 引理

2 关于不定方程xy+yz+zw+wr+rx=0的整数解

不定方程

xy+yz+zw+wr+rx=0

(1)

的解的情况比较复杂，将分以下情况进行讨论.

2.1 关于不定方程xyzwr=0的情况

(1)x，y，z，w，r中有一个为0.令x=0，y>0，z≠0，w≠0，r≠0，方程(1)变为yz+zw+wr=-1，yz>0，因此zw，wr中至少有一个为负.此时分3种情况进行讨论：①zw>0，wr<0；②zw<0，wr>0；③zw<0，wr<0.

① 当zw>0，wr<0时，w<0，r为奇数，00，yz为整数，zw+wr=-1-yz也为整数.若r<0，则-10，则wr>0为整数，zw=-1-yz-wr也为整数，即zw=1，z=1，y=-2-wr.令w=k1(k1<-1且为奇数)，r=k2(k2>0且为奇数)，方程(1)的解为(0，-2-k1k2，1，k1，k2)，(k2，0，-2-k1k2，1，k1)，(k1，k2，0，-2-k1k2，1)，(1，k1，k2，0，-2-k1k2)，(-2-k1k2，1，k1，k2，0).如果w为偶数，若z>0，r>0，则yz，wr为整数，zw=-1-yz-wr也为整数，即zw=1，z=1，y=-2-wr.令w=k3(k3<0且为偶数)，r=k4(k4>0且为奇数)，方程(1)的解为(0，-2-k3k4，1，k3，k4)，(k4，0，-2-k3k4，1，k3)，(k3，k4，0，-2-k3k4，1)， (1，k3k4，0，-2-k3k4)，(-2-k3k4，1，k3，k4，0)，当k3=-2时，k4为大于1的奇数.若z>0，r<0，则-1

③ 当zw<0，wr<0时，w<0，z<0，w，r为奇数，-1≤zw<0.若r<0，zw+wr=-1-yz，则zw，wr有一个为-1·zw=-1时，z=r=-1，y=-w，令w=k6(k6<0且为奇数)，方程(1)的解为(0，-k6，-1，k6，-1)，(-1，0，-k6，-1，k6)，(k6，-1，0，-k6，-1)，(-1，k6，-1，0，-k6)，(-k6，-1，k6，-1，0).wr=-1时，y=1，z=w=-1，r=k7(k7<0且为奇数)，方程(1)的解为(0，1，-1，-1，k7)，(k7，0，1，-1，-1)，(-1，k7，0，1，-1)，(-1，-1，k7，0，1)，(1，-1，-1，k7，0).若r>0，wr为整数，zw+yz=-1-wr必为整数，于是zw+yz=0，wr=-1，则y=1，z=w=-1，r=k8(k8>0且为奇数)，方程(1)的解为(0，1，-1，-1，k8)，(k8，0，1，-1，-1)，(-1，k8，0，1，-1)，(-1，-1，k8，0，1)，(1，-1，-1，k8，0).

(2)x，y，z，w，r中有两个为0，令x=0，z=0，y>0，w>0，r≠0，方程(1)为wr+2=0.即wr=-2与wr>0矛盾. 由于00没意义，所以x，y，z，w，r中不可能含有3个或3个以上的0.